
4.函数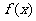 为奇函数且周期为3,
为奇函数且周期为3,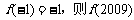 等于
(
)
等于
(
)
A.0 B.1 C.-1 D.2
3.已知A= B ={1,2,3,4,5},从A到B的映射f满足:(1)f(1)≤f(2)≤……≤f(5);(2)A中元素在B中的象有且只有2个,则适合条件的映射f的个数是 ( )
A.10 B.20 C.30 D.40
2.已知 的值是 ( )
的值是 ( )
A.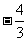 B.
B.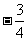 C.
C.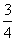 D.
D.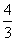
1.已知全集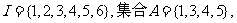
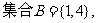
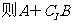 等于( )
等于( )
A.{1,4} B.{2,6} C.{3,5} D.{2,3,5,6}
22.(本小题满分12分)已知函数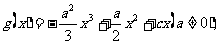
(I)当a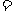 1时,若函数
1时,若函数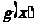 在区间
在区间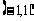 上是增函数,求实数
上是增函数,求实数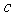 的取值范围;
的取值范围;
(II)当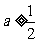 时,求证:对任意的
时,求证:对任意的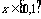 ,
,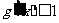 的充要条件是
的充要条件是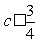 ;
;
21.(本小题满分12分)已知数列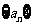 满足
满足
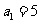 ,
, 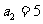 ,
,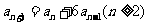 。
。
(1)求证: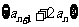 是等比数列;
是等比数列;
(2)求数列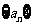 的通项公式;
的通项公式;
(3)设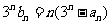 ,且
,且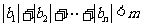 对于
对于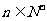 恒成立,求
恒成立,求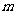 的取值范围.
的取值范围.
20.(本小题满分12分)设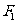 ,
,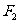 分别是椭圆
分别是椭圆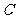 :
: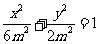
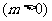 的左,右焦点.
的左,右焦点.
(1)当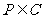 ,且
,且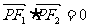 ,
,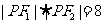 时,求椭圆C的左,右焦点
时,求椭圆C的左,右焦点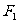 、
、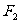
(2)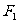 、
、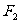 是(1)中的椭圆的左,右焦点,已知⊙F2的半径是1,过动点
是(1)中的椭圆的左,右焦点,已知⊙F2的半径是1,过动点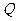 作⊙F2的切线
作⊙F2的切线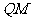 ,使得
,使得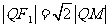 (
(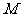 是切点),如下图,求动点
是切点),如下图,求动点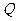 的轨迹方程.
的轨迹方程.
19.(本小题满分12分)
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2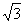 ,M、N分别为AB、SB的中点.
,M、N分别为AB、SB的中点.
(Ⅰ)证明:AC⊥SB;
(Ⅱ)求二面角N-CM-B的大小;
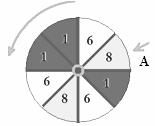
18.(本小题满分12分)如图,转盘游戏.转盘被分成8个均匀的扇形区域.游戏规则:用力旋转转盘,转盘停止时箭头A所指区域的数字就是游戏所得的点数(转盘停留的位置是随机的).假设箭头指到区域分界线的概率为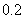 ,同时规定所得点数为0。某同学进行了一次游戏,记所得点数为
,同时规定所得点数为0。某同学进行了一次游戏,记所得点数为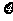 。求
。求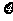 的分布列及数学期望。
的分布列及数学期望。
17.(本小题满分10分)
已知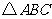 的周长为
的周长为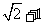 ,且
,且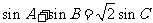 .
.
(I)求边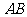 的长;
的长;
(II)若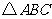 的面积为
的面积为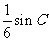 ,求角
,求角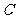 的度数.
的度数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com