
4.函数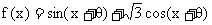 的图象关于点
的图象关于点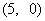 对称, 则
对称, 则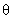 的值是( )
的值是( )
A.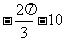 B.
B.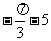
C.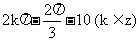 D.
D.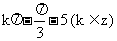
3.在等比数列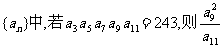 的值为( )
的值为( )
A.1 B.2 C.3 D.9
2.已知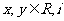 为虚数单位,且
为虚数单位,且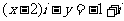 ,则
,则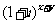 的值为( )
的值为( )
A.4
B. C.
C. D.
D.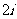
1.设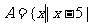 ≤4},
≤4},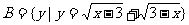 ,
,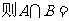 ( )
( )
A.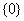 B.{3}
C.Ф D.
B.{3}
C.Ф D.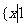 ≤
≤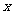 ≤
≤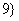
22.(本小题满分14分)
已知函数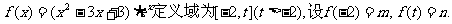
(I)试确定t的取值范围,使得函数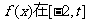 上为单调函数;
上为单调函数;
(II)求证: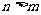 ;
;
(III)求证:对于任意的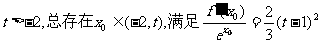 ,并确定这样的
,并确定这样的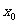 的个数。
的个数。
21.(本小题满分12分)
如图,F是椭圆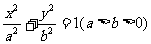 的一个焦点,A、B是椭圆的两个顶点,椭圆的离心率为
的一个焦点,A、B是椭圆的两个顶点,椭圆的离心率为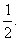 点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线
点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线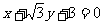 相切。
相切。
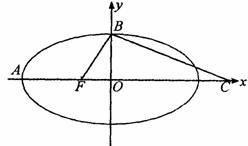
(I)求椭圆的方程;
(II)过F作一条与两坐标轴都不垂直的直线l交椭圆于P、Q两点,在x轴上是否存在点N,使得NF恰好为△PNQ的内角平分线,若存在,求出点N的坐标,若不存在,请说明理由。
20.(本小题满分12分)
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°。
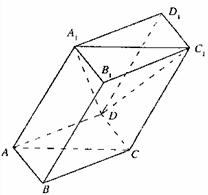
(I)证明:BD⊥AA1;
(II)求二面角D-A1A-C的平面角的余弦值;
(III)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
19.(本小题满分12分)
袋中装有大致相同的黑球、白球和红球共10个。已知从袋中任意摸出1个球,得到黑球的概率是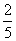 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是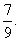
(I)求袋中各色球的个数;
(II)从袋中任意摸出3个球,记得到白球的个数为ξ,求随机变量ξ的分布列及数学期望Eξ和方差Dξ;
(III)若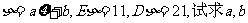 的值。
的值。
18.(本小题满分12分)
已知数列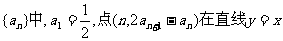 上,其中n=1、2、3…。
上,其中n=1、2、3…。
(I)令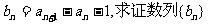 是等比数列;
是等比数列;
(II)求数列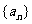 的通项。
的通项。
17.(本小题满分12分)
已知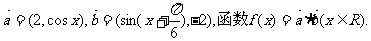
(I)求函数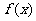 的单调增区间;
的单调增区间;
(II)若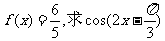 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com