
19.(本小题满分12分)
如图,四面体ABCD中,三角形ABC与三角形DBC都是边长为4的正三角形。
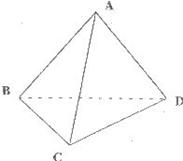
(1)求证:BC⊥AD
(2)若点D到平面ABC的距离不小于3,求二面角A-BC-D的平面角的取值范围。
(3)当二面角A-BC-D的平面角为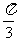
 时,求点C到平面ABD的距离。
时,求点C到平面ABD的距离。
18.(本小题满分12分)
设函数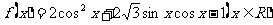 的最大值为M,最小正周期为T。
的最大值为M,最小正周期为T。
(1)求M、T;
(2)10个互不相等的正数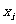 满足
满足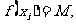 且
且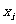 <10
<10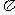
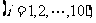 求
求 的值。
的值。
17.(本小题满分12分)
在袋里装30个小球,其中彩球有:n个红色,5个蓝色,10个黄色,其余为白色。求:
(1)如果已经从中取定了5个黄球和3个蓝球,并将它们编上了不同的号码后排成一排,那么使蓝色小球互不相邻的排法有多少种?
(2)如果从袋里取出3个都是相同颜色的彩球(无白色)的概率是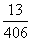 且
且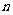 ≥2,计算红球有几个?
≥2,计算红球有几个?
(3)根据(2)的结论,计算从袋中任取3个小球至少有一个是红球的概率。
16.记二项式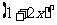 展开式中的各项系数和为
展开式中的各项系数和为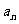 ,二项式系数之和为
,二项式系数之和为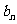 ,则
,则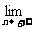
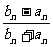 的极限为
的极限为
15.已知函数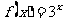 的反函数是
的反函数是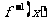 ,且
,且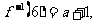 那么函数
那么函数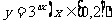 的值域为
的值域为
14.在一张硬纸上,挖去一个半径为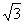 的圆洞,然后把此洞套在一个底面边长为4,高为6的正三棱锥上,并使纸面与锥底平行,则能穿过纸面的棱锥的高的最大值等于
的圆洞,然后把此洞套在一个底面边长为4,高为6的正三棱锥上,并使纸面与锥底平行,则能穿过纸面的棱锥的高的最大值等于
13.若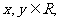 且
且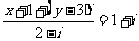 ,则
,则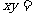

12.有A、B、C、D、E、F六人依次站在正六边形的六个顶点处传球,从A开始,每次可随意传给相邻的两人之一,若在5次之内传到D,则停止传球;若在5次之内传不到D,则传完5次也停止传球,那么从开始到停止,可能出现的传法种数是 ( )
( )
A.24 B.26 C.30 D.28
11.定义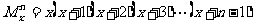 ,其中
,其中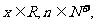 则函数
则函数
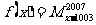 的奇偶性为
的奇偶性为 ( )
( )
A.是奇函数不是偶函数 B.是偶函数不是奇函数
C.既是奇函数又是偶函数 D.既非奇函数又非偶函数
10.已知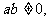 点M
点M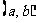 是圆
是圆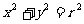 内一点,直线m是以点M为中点的弦所在的直线,直线
内一点,直线m是以点M为中点的弦所在的直线,直线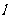 的方程为
的方程为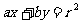 ,则下列结论正确的是
,则下列结论正确的是 ( )
( )
A.m∥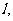 且
且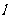 与圆相交 B.
与圆相交 B.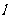 ⊥
⊥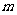 ,且
,且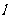 与圆相切
与圆相切 
C.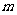 ∥
∥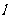 ,且
,且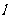 与圆相离 D.
与圆相离 D.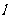 ⊥
⊥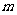 ,且
,且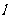 与圆相离
与圆相离
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com