
2.如果复数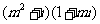 是实数,则实数
是实数,则实数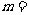 ( )
( )
A.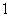 B.
B.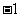 C.
C.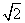 D.
D.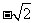
1.已知集合A=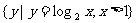 ,B=
,B=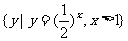 ,则A
,则A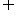 B=[ ]
B=[ ]
A.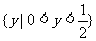 B.
B.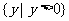 C.
C.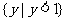 D.
D.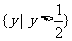
22.(14分)已知数列{a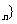 的前n项和为S
的前n项和为S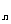 ,满足S
,满足S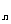 =2a
=2a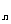 -2n(n∈N
-2n(n∈N )
)
(1)求数列{a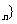 的通项公式a
的通项公式a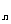 ;
;
(2)若数列{b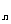 }满足b
}满足b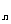 =log
=log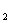 (a
(a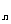 +2),T
+2),T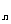 为数列{
为数列{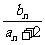 }的前n项和,求证T
}的前n项和,求证T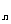 ≥
≥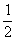 .
.
(3)数列{a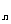 }中是否存在三项a
}中是否存在三项a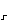 ,a
,a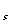 ,a
,a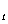 (r<s<t
(r<s<t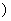 成等差数列?或存在,请求出一组适合条件的项;若不存在,请说明理由.
成等差数列?或存在,请求出一组适合条件的项;若不存在,请说明理由.
21.已知函数f(x)=-x3+3x2+ax+b在 点(1,f(1))处的切线与直线12x-y-1=0 平行.
(1)求实数a的值;
(2)求f(x)的单调递减区间;
(3)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.(12分)
20.用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用1个单位量的水可清除蔬菜上残留农药量的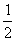 ,用水越多,洗掉的农药量也越多,但总还有农药残留在蔬菜上,设用x单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
,用水越多,洗掉的农药量也越多,但总还有农药残留在蔬菜上,设用x单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数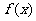 。(12分)
。(12分)
(1)那么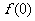 =____________;其实际意义是____________________________________.
=____________;其实际意义是____________________________________.
(2)函数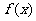 的值域是_______________,单调性是_____________________.
的值域是_______________,单调性是_____________________.
(3)若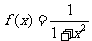 ,现在用a单位的水,可以清洗一次,也可以平均分成两份后清洗两次,哪种方案清洗后蔬菜上残留的农药量比较少?说明理由.
,现在用a单位的水,可以清洗一次,也可以平均分成两份后清洗两次,哪种方案清洗后蔬菜上残留的农药量比较少?说明理由.
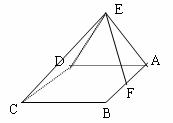
19.如图,边长为2的正三角形ADE垂直于矩形ABCD所在平面,F是AB的中点,EC和平面ABCD成45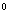 角.(1)求四棱锥E-AFCD的体积;(2)求二面角E-FC-D的大小;(3)求D到平面EFC的距离.(12分)
角.(1)求四棱锥E-AFCD的体积;(2)求二面角E-FC-D的大小;(3)求D到平面EFC的距离.(12分)
18.函数f(x)=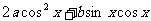 满足
满足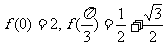
(1)若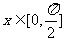 ,求
,求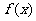 的最大值和最小值;
的最大值和最小值;
(2)若要得到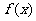 的图象,需将
的图象,需将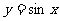 的图象作怎样的变化?(12分)
的图象作怎样的变化?(12分)
17.已知命题P:不等式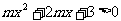 在R上恒成立;命题q:函数
在R上恒成立;命题q:函数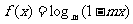 在区间[0,2]是增函数.求实数
在区间[0,2]是增函数.求实数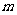 的取值范围,使“P或q”为真命题,“P 且q”为假命题.(12分)
的取值范围,使“P或q”为真命题,“P 且q”为假命题.(12分)
16.若面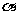 经过
经过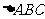 的重心,且A、B在
的重心,且A、B在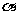 的同侧到
的同侧到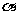 的距离分别为2,4,那么C到
的距离分别为2,4,那么C到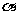 的距离是
.
的距离是
.
15.某人射击一次击中的概率为0.6 , 经过3次射击,此人至少有两次击中目标的概率为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com