
20.(本小题满13分)定义在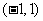 上的函数
上的函数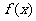 满足:
满足: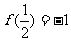 ,对任意的
,对任意的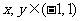 都有
都有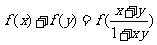 ,数列
,数列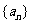 满足:
满足: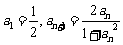 ,设
,设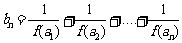
(1)求证:函数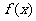 是奇函数;
是奇函数;
(2)求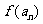 的解析式;
的解析式;
(3)是否存在自然数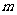 ,使得对任意
,使得对任意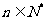 ,都有
,都有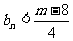 成立,若存在,求出
成立,若存在,求出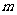 的最小值,若不存在,说明理由。
的最小值,若不存在,说明理由。
19.(本小题13分)曲线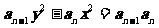 的一个焦点为
的一个焦点为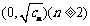 ,且
,且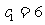 ,一条渐近线方程为
,一条渐近线方程为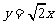 , 其中
, 其中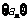 是以4为首项的正数数列.
是以4为首项的正数数列.
(I)求数列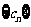 的通项公式;
的通项公式;
(II)求证:不等式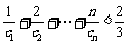 对一切自然数
对一切自然数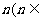 N*)恒成立。
N*)恒成立。
18.(本小题12分)如图,四棱锥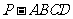 的底面
的底面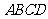 是正方形,侧棱
是正方形,侧棱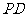 ⊥底面
⊥底面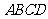 ,
,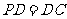 ,
,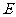 是
是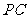 的中点。
的中点。
(Ⅰ)证明: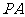 ∥平面
∥平面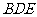 ;
;
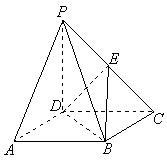
(Ⅱ)求二面角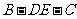 的大小;
的大小;
(Ⅲ)在棱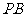 上找一点
上找一点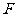 ,当
,当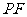 :
: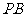 为何值时? 使得
为何值时? 使得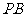 ⊥平面
⊥平面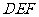 。
。
17.(本小题12分)已知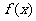 是二次函数,不等式
是二次函数,不等式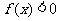 的解集是
的解集是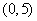 ,且
,且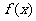 在区间
在区间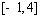 上的最大值是12.
上的最大值是12.
(Ⅰ)求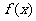 的解析式;
的解析式;
(Ⅱ)解关于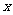 的不等式
的不等式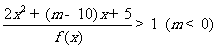 .
.
16.(本小题12分)在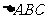 中,角
中,角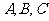 的对边分别为
的对边分别为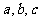 ,且
,且
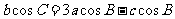
|
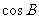 的值; (2)若
的值; (2)若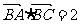 ,
,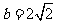 ,求
,求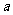 和
和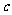 的值。
的值。15.已知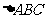 的面积为
的面积为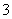 ,且满足
,且满足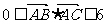 ,则函数
,则函数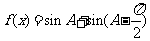 的最大值为_ __
的最大值为_ __
14.在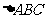 中,已知
中,已知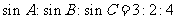 ,则
,则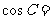 ________
________
13.已知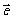 是单位向量,
是单位向量,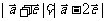 ,则
,则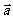 在
在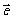 方向上的投影是___________
方向上的投影是___________
12.某公司一年购买某种货物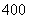 吨,每次都购买
吨,每次都购买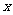 吨,运费为
吨,运费为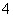 万元,一年的总存储费用为
万元,一年的总存储费用为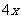 万元,要使一年的总费用与总存储费用之和最小,则
万元,要使一年的总费用与总存储费用之和最小,则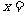 ___________
___________
11.函数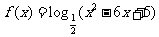 的单调递增区间为
的单调递增区间为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com