
8.要得到函数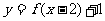 的图象,只需将函数
的图象,只需将函数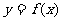 的图象( )
的图象( )
A.向右平移2个单位,向下平移l个单位.
B.向左平移2个单位,向下平移1个单位.
C.向右平移2个单位,向上平移1个单位.
D.向左平移2个单位,向上平移1个单位.
9,设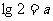 ,
,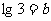 ,则
,则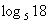 等于( )
等于( )
A.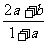 B.
B.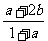 C.
C.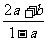 D.
D.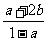
7.函数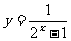 的值域是( )
的值域是( )
A.(-∞,1) B.(-∞,0)∪(0,+∞)
C.(-1,+∞) D.(-∞,-1)∪(0,+∞)
6.已知函数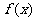 的图像是连续不断的,有如下的
的图像是连续不断的,有如下的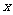 ,
,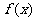 对应值表:
对应值表:
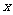 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
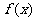 |
123.5 |
21.5 |
-7.82 |
11.57 |
-53.7 |
-126.7 |
-l29.6 |
那么函数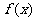 在区间[1,6]上的零点至少有( )
在区间[1,6]上的零点至少有( )
A.2个 B.3个 C.4个 D.5个
5.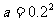 ,
,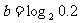 ,
,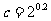 之间的大小关系是( )
之间的大小关系是( )
A.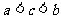 B.
B.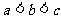 C.
C.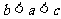 D.
D.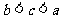
4.不等式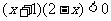 的解集为( )
的解集为( )
A.{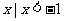 或
或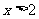 } B.{
} B.{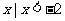 或
或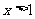 }
}
C.{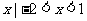 } D.{
} D.{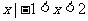 }
}
3.(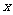 ,y)在映射
,y)在映射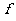 下的象是
下的象是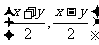 ,则(-5,2)的原象是( )
,则(-5,2)的原象是( )
A.(-10,4) B.(-3,-7)
C.(-6,-4) D.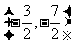
2.下列函数与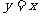 有相同图象的一个是( )
有相同图象的一个是( )
A.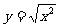 B.
B.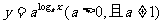
C.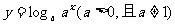 D.
D.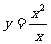
1.下列几个关系中正确的是( )
A.0∈{0} B.0={0} C.0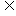 {0} D.
{0} D.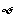 ={0}
={0}
22.(本小题共14分)已知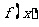 是定义在实数集R上的不恒为
是定义在实数集R上的不恒为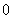 的函数,对任意实数
的函数,对任意实数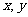 有
有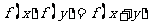 ,当
,当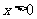 时,有
时,有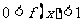 .
.
(Ⅰ)求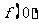 的值,并证明
的值,并证明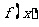 恒正;
恒正;
(Ⅱ)判断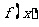 在实数集R上单调性;
在实数集R上单调性;
(Ⅲ)设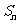 为数列
为数列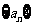 的前
的前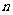 项和,
项和,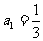 ,
, (
(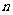 为正整数).令
为正整数).令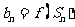 ,问数列
,问数列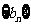 中是否存在最大项?若存在,求出最大项的值;若不存在,试说明理由.
中是否存在最大项?若存在,求出最大项的值;若不存在,试说明理由.
21.(本小题共12分) 已知函数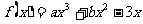 (
(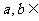 R),且
R),且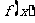 在
在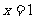 和
和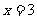 处取得极值.
处取得极值.
(Ⅰ)求函数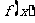 的解析式;
的解析式;
(Ⅱ)设函数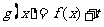 ,是否存在实数
,是否存在实数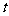 ,使得曲线
,使得曲线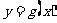 与
与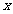 轴有两个交点,若存在,求
轴有两个交点,若存在,求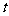 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com