
20.(本小题共12分) 某超市计划销售一种水果,已知水果的进价为每盒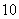 元,并且水果的进货量由销售量决定.预计这种水果以每盒
元,并且水果的进货量由销售量决定.预计这种水果以每盒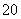 元的价格销售时该超市可销售
元的价格销售时该超市可销售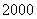 盒,经过市场调研发现每盒水果的价格在每盒
盒,经过市场调研发现每盒水果的价格在每盒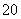 元的基础上每减少一元则增加销售
元的基础上每减少一元则增加销售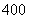 盒,而每增加一元则减少销售
盒,而每增加一元则减少销售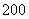 盒,现设每盒水果的销售价格为
盒,现设每盒水果的销售价格为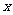
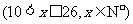 元.
元.
(Ⅰ)求销售这种水果所获得的利润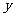 (元)与每盒水果的销售价格
(元)与每盒水果的销售价格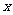 的函数关系式;
的函数关系式;
(Ⅱ)当每盒水果的销售价格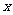 为多少元时,销售这种水果所获得的利润
为多少元时,销售这种水果所获得的利润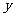 (元)最大,并求出最大值.
(元)最大,并求出最大值.
19.(本小题共12分)
在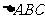 中,角
中,角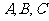 所对的边分别是
所对的边分别是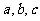 ,且
,且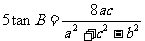 .
.
(I) 求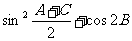 的值;
的值;
(Ⅱ)若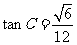 ,
,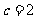 ,求
,求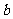 的值.
的值.
18.(本小题共12分)已知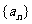 是首项为
是首项为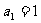 的等差数列且满足
的等差数列且满足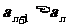
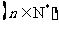 ,等比数列
,等比数列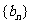 的前三项分别为
的前三项分别为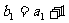 ,
,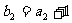 ,
,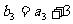 .
.
(Ⅰ)求数列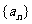 和
和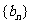 的通项公式;
的通项公式;
(Ⅱ)若数列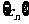 满足
满足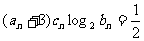 ,求数列
,求数列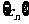 的前
的前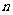 项和
项和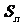 .
.
17.(本小题共12分) 已知向量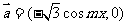 ,向量
,向量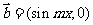 ,函数
,函数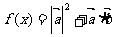 的最小正周期为
的最小正周期为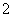 ,其中
,其中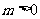 .
.
(Ⅰ)求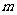 的值;
的值;
(Ⅱ)求当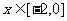 时
时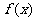 的单调递增区间.
的单调递增区间.
16.对于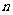 个向量
个向量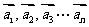 ,若存在
,若存在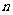 个不全为零的实数
个不全为零的实数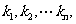 使得:
使得:
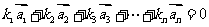 成立,则称向量
成立,则称向量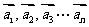 是线性相关的.按此规定,能使向量
是线性相关的.按此规定,能使向量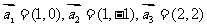 是线性相关的实数为
是线性相关的实数为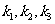 ,则
,则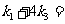 .
.
15.已知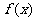 是定义在
是定义在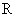 上的偶函数,并且
上的偶函数,并且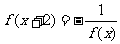 ,当
,当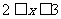 时,
时,
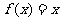 ,则
,则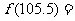 _________________.
_________________.
14.已知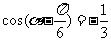 ,则
,则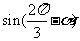 的值为 .
的值为 .
13.若等比数列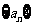 的前
的前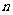 项和
项和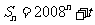 (
(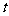 为常数),则
为常数),则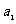 的值为 .
的值为 .
12.设函数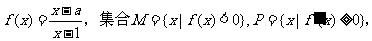
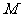 是
是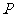 的真子集,则实数
的真子集,则实数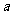 的取值范围是 ( )
的取值范围是 ( )
A. B.
B.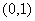 C.
C.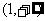 D.
D.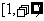
第Ⅱ卷(非选择题 共90分)
11.已知函数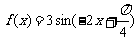 的图象,给出以下四个论断:
的图象,给出以下四个论断:
①该函数图象关于直线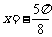 对称;
对称;
②该函数图象的一个对称中心是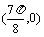 ;
;
③函数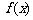 在区间
在区间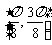 上是减函数;
上是减函数;
④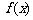 可由
可由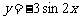 向左平移
向左平移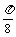 个单位得到.以上四个论断中正确的个数为( )
个单位得到.以上四个论断中正确的个数为( )
A.1 B.2 C.3 D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com