
14.将给定的25个数排成如右图所示的数表,若每行5个数按从左至右的顺序构成等差数列,每列的5个数按从上到下的顺序也构成等差数列,且表正中间一个数a33=1,则表中所有数之和为
11.将容量为50的样本数据,按从小到大的顺序分成4组,如下表:
|
组号 |
1 |
2 |
3 |
4 |
|
频数 |
11 |
14 |
|
13 |
则第3组的频率为
12 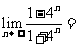
 13 圆
13 圆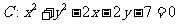 的圆心坐标为
,设
的圆心坐标为
,设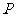 是该圆的过点
是该圆的过点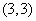 的弦的中点,则动点
的弦的中点,则动点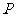 的轨迹方程是
的轨迹方程是
1在复平面内,复数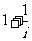 所对应的点位于
所对应的点位于
A.第一象限 B第二象限 C.第三象限 D第四象限
2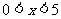 是不等式
是不等式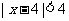 成立的
成立的
A.充分不必要条件 B必要不充分条件
C.充要条件 D既不充分也不必要条件
3 已知直线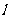 及三个平面
及三个平面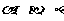 ,给出下列命题:
,给出下列命题:
①若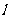 //
//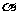 ,
, //
//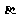 ,则
,则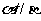 ②若
②若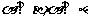 ,则
,则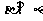
③若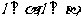 则
则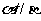 ④若
④若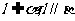 ,则
,则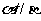
其中真命题是
A ①
B
②
C ③ D ④
D ④
4 已知实数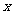 、
、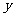 满足约束条件
满足约束条件 ,则
,则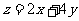 的最大值为
的最大值为
A 24 B 20 C 16 D 12
5 已知R上的奇函数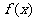 在区间(-∞,0)内单调增加,且
在区间(-∞,0)内单调增加,且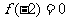 ,则不等式
,则不等式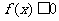 的解集为
的解集为
A 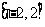 B
B 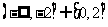
C 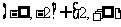 D
D 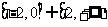
6 某学校要派遣6位教师中的4位去参加一个学术会议,其中甲、乙两位教师不能同时参加,则派遣教师的不同方法数共有
A.7种 B.8种 C.9种 D.10种
7 按向量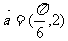 平移函数
平移函数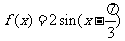 的图象,得到函数
的图象,得到函数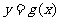 的图象,则
的图象,则
A 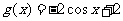 B
B
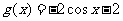
C 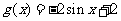 D
D
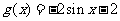
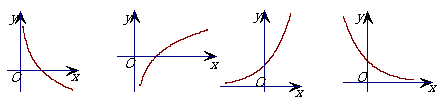 8 函数
8 函数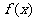 (
(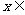 R)由
R)由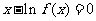 确定,则导函数
确定,则导函数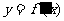 图象的大致形状是
图象的大致形状是
A B C D
9 曲线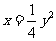 上的点
上的点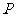 到点
到点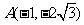 与到
与到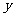 轴的距离之和为
轴的距离之和为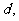 则
则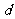 的最小值是
的最小值是
A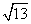 B
B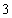 C
C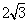 D
D
10 若点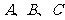 是半径为
是半径为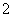 的球面上三点,且
的球面上三点,且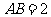 ,则球心到平面
,则球心到平面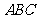 的距离之最大值为
的距离之最大值为
A 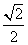 B
B 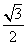 C
C
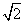 D
D 
第Ⅱ卷(非选择题共100分)
第Ⅱ卷全部是非选择题,必须在答题卡非选择题答题区域内,用黑色钢笔或签字笔作答,不能答在试卷上,否则答案无效.
演算步骤。
(17)(本小题满分10分)
甲、乙二人参加普法知识竞答,共有10个不同的题目,其中选择题6个,判断题4个。甲、乙二人依次各抽一题。
(I)甲抽到选择题、乙抽到判断题的概率是多少?
(II)甲、乙二人中至少有一人抽到选择题的概率是多少?
(18)(本小题满分12分)
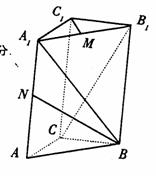
如图,直三棱柱ABC-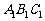 ,底面ΔABC中,CA=CB=1,BCA=
,底面ΔABC中,CA=CB=1,BCA=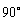 ,棱
,棱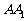 =2,M、N分别是
=2,M、N分别是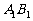 、
、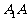 的中点。
的中点。
(I)求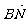 的长;(II)求
的长;(II)求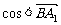 ,
,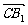
 的值;
的值;
(III)求证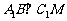 。
。
(19)(本小题满分12分)
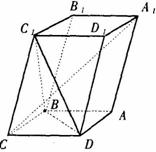
如图,已知平行六面体ABCD-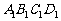 的底面ABCD是菱形,且
的底面ABCD是菱形,且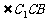 =
=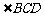 =
=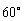 。
。
(I)证明: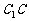 ⊥BD;
⊥BD;
(II)假定CD=2,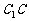 =
=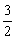 ,记面
,记面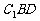 为
为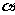 ,面CBD为
,面CBD为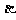 ,求二面角
,求二面角 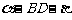 的平面角的余弦值;
的平面角的余弦值;
(III)当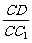 的值为多少时,能使
的值为多少时,能使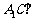 平面
平面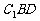 ?请给出证明。
?请给出证明。
(20)(本小题满分12分)
设函数 ,其中
,其中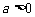 。
。
(I)解不等式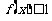 ;
;
(II)求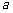 的取值范围,使函数
的取值范围,使函数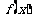 在区间
在区间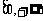 上是单调函数。
上是单调函数。
(21)(本小题满分12分)
用总长14.8m的钢条制成一个长方体容器的框架,如果所制做容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积。
(22)(本小题满分12分)
(I)已知数列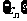 ,其中
,其中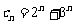 ,且数列
,且数列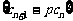 为等比数列,求常数
为等比数列,求常数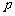 。
。
(II)设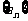 、
、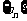 是公比不相等的两个等比数列,
是公比不相等的两个等比数列, ,证明数列
,证明数列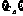 不是等比数列。
不是等比数列。
(23)(本小题满分14分)
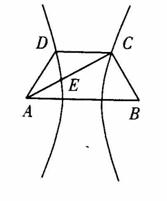
如图,已知梯形ABCD中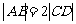 ,点E分有向线段
,点E分有向线段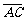 所成的比为
所成的比为 ,双曲线过C、D、E三点,且以A、B为焦点。当
,双曲线过C、D、E三点,且以A、B为焦点。当 时,求双曲线离心率
时,求双曲线离心率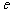 的取值范围。
的取值范围。
(13)某厂生产电子元件,其产品的次品率为5%,现从一批产品中任意地连续取出2件,其中次品 的概率分布是
的概率分布是
 |
0 |
1 |
2 |
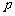 |
|
|
|
(14)椭圆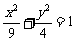 的焦点为
的焦点为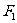 、
、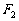 ,点P为其上的动点,当
,点P为其上的动点,当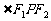 为钝角时,点P横坐标的取值范围是________。
为钝角时,点P横坐标的取值范围是________。
(15)设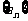 是首项为1的正项数列,且
是首项为1的正项数列,且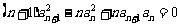 (
(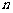 =1,2 3,…),则它的通项公式是
=1,2 3,…),则它的通项公式是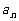 =________。
=________。
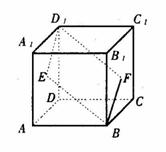
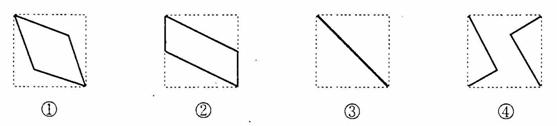
(16)如图,E、F分别为正方体的面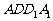 、面
、面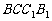 的中心,则四边形
的中心,则四边形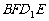 在该正方体的面上的射影可能是_______。(要求:把可能的图的
序号都填上)
在该正方体的面上的射影可能是_______。(要求:把可能的图的
序号都填上)
22.(本小题满分14分)已知数列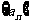 的前
的前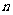 项和
项和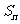 满足
满足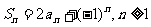 .
.
(1)写出数列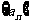 的前三项
的前三项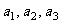 ;
;
(2)求数列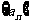 的通项公式;
的通项公式;
(3)证明:对任意的整数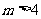 ,有
,有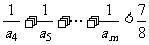 .
.
21.(本小题满分12分)设椭圆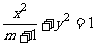 的两个焦点是
的两个焦点是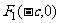 与
与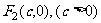 ,且椭圆上存在一点
,且椭圆上存在一点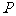 ,使得直线
,使得直线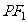 与
与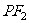 垂直.
垂直.
(1)求实数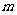 的取值范围;
的取值范围;
(2)设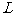 是相应于焦点
是相应于焦点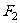 的准线,直线
的准线,直线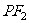 与
与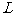 相交于点
相交于点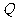 ,若
,若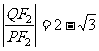 ,求直线
,求直线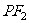 的方程.
的方程.
20.(本小题满分12分)
三棱锥P-ABC中,侧面PAC与底面ABC垂直,PA=PB=PC=3,
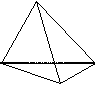
(1)求证:AB ⊥ BC;
(2)设AB=BC=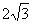 ,求AC与平面PBC所成角的大小.
,求AC与平面PBC所成角的大小.
19.(本小题满分12分)某村计划建造一个室内面积为800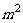 的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1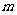 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3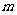 宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
18.(本小题满分12分)解方程 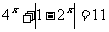 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com