
(13)在下列关于直线l、m与平面α、β的命题中,真命题是
(A)若l β且α⊥β,则l⊥α. (B)若l⊥β且α∥β,则l⊥α.
β且α⊥β,则l⊥α. (B)若l⊥β且α∥β,则l⊥α.
(C)若l⊥β且α⊥β,则l∥α. (D)若α∩β=m且l∥m,则l∥α.
(14)三角方程2sin(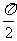 -x)=1的解集为
-x)=1的解集为
(A){x│x=2kπ+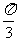 ,k∈Z}. (B){x│x=2kπ+
,k∈Z}. (B){x│x=2kπ+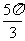 ,k∈Z}.
,k∈Z}.
(C){x│x=2kπ±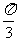 ,k∈Z}. (D){x│x=kπ+(-1)K,k∈Z}.
,k∈Z}. (D){x│x=kπ+(-1)K,k∈Z}.
(15)若函数y=f(x)的图像可由函数y=lg(x+1)的图像绕坐标原点O逆时针旋转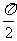 得到,则f(x)=
得到,则f(x)=
(A)10-x-1. (B)10x-1.
(C)1-10-x. (D)1-10x.
(16)某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
|
行业名称 |
计算机 |
机械 |
营销 |
物流 |
贸易 |
|
应聘人数 |
215830 |
200250 |
154676 |
74570 |
65280 |
|
行业名称 |
计算机 |
营销 |
机械 |
建筑 |
化工 |
|
招聘人数 |
124620 |
102935 |
89115 |
76516 |
70436 |
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是
(A)计算机行业好于化工行业. (B)建筑行业好于物流行业.
(C)机械行业最紧张. (D)营销行业比贸易行业紧张.
(1)若tgα=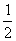 ,则tg(α+
,则tg(α+ )= .
)= .
(2)设抛物线的顶点坐标为(2,0),准线方程为x=-1,则它的焦点坐标为 .
(3)设集合A={5,log2(a+3)},集合B={a,b}.若A∩B={2},则A∪B= .
(4)设等比数列{an}(n∈N)的公比q=-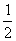 ,且
,且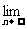 (a1+a3+a5+…+a2n-1)=
(a1+a3+a5+…+a2n-1)=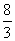 ,则a1= .
,则a1= .
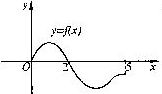
(5)设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时, f(x)的图像如右图,则不等式f(x)<0的解是 .
(6)已知点A(1, -2),若向量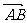 与
与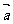 ={2,3}同向,
={2,3}同向,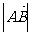 =2
=2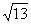 ,则点B的坐标为
.
,则点B的坐标为
.
(7)在极坐标系中,点M(4,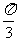 )到直线l:ρ(2cosθ+sinθ)=4的距离d= .
)到直线l:ρ(2cosθ+sinθ)=4的距离d= .
(8)圆心在直线2x-y-7=0上的圆C与y轴交于两点A(0, -4),B(0, -2),则圆C的方程为 .
(9)若在二项式(x+1)10的展开式中任取一项,则该项的系数为奇数的概率是 . (结果用分数表示)
(10)若函数f(x)=a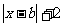 在[0,+∞]上为增函数,则实数a、b的取值范围是
.
在[0,+∞]上为增函数,则实数a、b的取值范围是
.
(11)教材中“坐标平面上的直线”与“圆锥曲线”两章内容体现出解析几何的本质是
.
(12)若干个能唯一确定一个数列的量称为该数列的“基本量”.设{an}是公比为q的无穷等比数列,下列{an}的四组量中,一定能成为该数列“基本量”的是第 组.(写出所有符合要求的组号)
①S1与S2; ②a2与S3; ③a1与an; ④q与an.
其中n为大于1的整数, Sn为{an}的前n项和.
(17)(本小题满分12分)
已知 的值.
的值.
(18)(本小题满分12分)
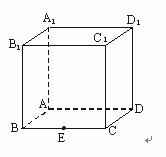
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.
(I)试确定点F的位置,使得D1E⊥平面AB1F;
(II)当D1E⊥平面AB1F时,求二面角C1-EF-A的大小(结果用反三角函数值表示).
(19)(本小题满分12分)
如图,在Rt△ABC中,已知BC=a,若长为2a的线段PQ以点A为中点,问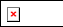 的夹角
的夹角 取何值时
取何值时 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.
(20)(本小题满分12分)
直线 的右支交于不同的两点A、B.
的右支交于不同的两点A、B.
(I)求实数k的取值范围;
(II)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
(21)(本小题满分12分)
某突发事件,在不采取任何预防措施的情况下发生的概率为0.3,一旦发生,将造成400万元的损失. 现有甲、乙两种相互独立的预防措施可供采用. 单独采用甲、乙预防措施所需的费用分别为45万元和30万元,采用相应预防措施后此突发事件不发生的概率为0.9和0.85. 若预防方案允许甲、乙两种预防措施单独采用、联合采用或不采用,请确定预防方案使总费用最少.
(总费用=采取预防措施的费用+发生突发事件损失的期望值.)
(22)(本小题满分14分)
已知
(I)已知数列 极限存在且大于零,求
极限存在且大于零,求 (将A用a表示);
(将A用a表示);
(II)设
(III)若 都成立,求a的取值范围.
都成立,求a的取值范围.
(13)设随机变量 的概率分布
的概率分布 .
.
(14)将标号为1,2,…,10的10个球放入标号为1,2,…,10的10个盒子内,每个盒内放一个球,则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有 种.(以数字作答)
(15)设A、B为两个集合,下列四个命题:
①A B 对任意
对任意 ②A B
②A B
③A B A
A B ④A B
B ④A B 存在
存在
其中真命题的序号是 .(把符合要求的命题序号都填上)
(16)某日中午12时整,甲船自A处以16km/h的速度向正东行驶,乙船自A的正北18km处以24km/h的速度向正南行驶,则当日12时30分时两船之间距间对时间的变化率是 km/h.
(1)与直线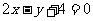 的平行的抛物线
的平行的抛物线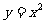 的切线方程是
的切线方程是
(A)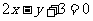 (B)
(B)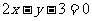
(C)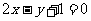 (D)
(D)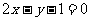
(2)复数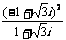 的值是
的值是
(A)-16 (B)16 (C)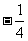 (D)
(D)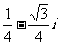
(3)已知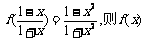 的解析式可取为
的解析式可取为
(A)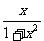 (B)
(B)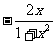 (C)
(C)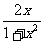 (D)
(D)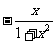
(4)已知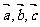 为非零的平面向量. 甲:
为非零的平面向量. 甲: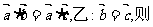
(A)甲是乙的充分条件但不是必要条件
(B)甲是乙的必要条件但不是充分条件
(C)甲是乙的充要条件
(D)甲既不是乙的充分条件也不是乙的必要条件
(5)若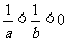 ,则下列不等式①
,则下列不等式①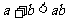 ;②
;②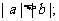 ③
③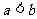 ;④
;④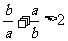 中,正确的不等式有
中,正确的不等式有
(A)1个 (B)2个 (C)3个 (D)4个
(6)已知椭圆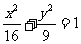 的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为
的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为
(A)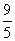 (B)3 (C)
(B)3 (C)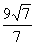 (D)
(D)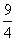
(7)函数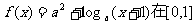 上的最大值和最小值之和为a,则a的值为
上的最大值和最小值之和为a,则a的值为
(A)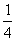 (B)
(B)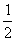 (C)2 (D)4
(C)2 (D)4
(8)已知数列{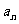 }的前n项和
}的前n项和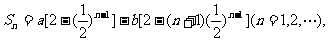 其中a、b是非零常数,则存在数列{
其中a、b是非零常数,则存在数列{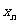 }、{
}、{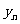 }使
}使
(A)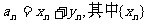 为等差数列,{
为等差数列,{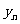 }为等比数列
}为等比数列
(B)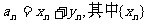 和{
和{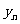 }都为等差数列
}都为等差数列
(C)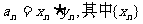 为等差数列,{
为等差数列,{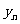 }都为等比数列
}都为等比数列
(D)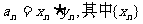 和{
和{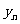 }都为等比数列
}都为等比数列
(9)函数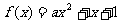 有极值的充要条件是
有极值的充要条件是
(A) (B)
(B)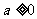 (C)
(C)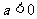 (D)
(D)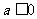
(10)设集合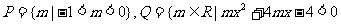 对任意实数x恒成立},则下列关系中成立的是
对任意实数x恒成立},则下列关系中成立的是
(A)P Q (B)Q P (C)P=Q (D)P Q=
Q=
(11)已知平面 所成的二面角为80°,P为
所成的二面角为80°,P为 、
、 外一定点,过点P的一条直线与
外一定点,过点P的一条直线与 、
、 所成的角都是30°,则这样的直线有且仅有
所成的角都是30°,则这样的直线有且仅有
(A)1条 (B)2条 (C)3条 (D)4条
(12)设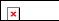 是某港口水的深度y(米)关于时间t(时)的函数,其中
是某港口水的深度y(米)关于时间t(时)的函数,其中 .下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
|
t |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y |
12 |
15.1 |
12.1 |
9.1 |
11.9 |
14.9 |
11.9 |
8.9 |
12.1 |
经长期观察,函数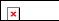 的图象可以近似地看成函数
的图象可以近似地看成函数 的图象.下面的函数中,最能近似表示表中数据间对应关系的函数
的图象.下面的函数中,最能近似表示表中数据间对应关系的函数
(A) (B)
(B)
(C) (D)
(D)
(17)(本小题满分12分)
设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx, 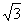 sin2x),x∈R.
sin2x),x∈R.
(Ⅰ)若f(x)=1-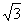 且x∈[-
且x∈[-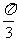 ,
,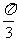 ],求x;
],求x;
(Ⅱ)若函数y=2sin2x的图象按向量c=(m,n)(|m|<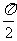 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
(18)(本小题满分12分)
甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.
(Ⅰ)求甲答对试题数ξ的概率分布及数学期望;
(Ⅱ)求甲、乙两人至少有一人考试合格的概率.
(19)(本小题满分12分)
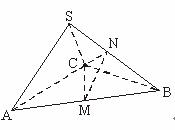
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2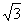 ,M、N分别为AB、SB的中点.
,M、N分别为AB、SB的中点.
(Ⅰ)证明:AC⊥SB;
(Ⅱ)求二面角N-CM-B的大小;
(Ⅲ)求点B到平面CMN的距离.
(20)(本小题满分12分)
某企业2003年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+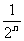 )万元(n为正整数).
)万元(n为正整数).
(Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为An万元,进行技术改造后的累计纯利润为Bn万元(须扣除技术改造资金),求An、Bn的表达式;
(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
(21)(本小题满分14分)
已知f(x)=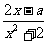 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)=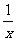 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
(22)(本小题满分12分)
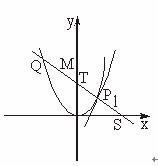
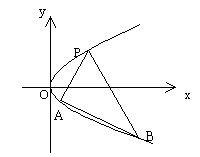
如图,P是抛物线C:y=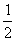 x2上一点,直线l过点P且与抛物线C交于另一点Q.
x2上一点,直线l过点P且与抛物线C交于另一点Q.
(Ⅰ)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求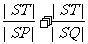 的取值范围.
的取值范围.
(13)直线x+2y=0被曲线x2+y2-6x-2y-15=0所截得的弦长等于 .
(x≠0),
(14)设函数f(x)= 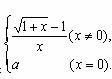 在x=0处连续,则实数a的值为
.
在x=0处连续,则实数a的值为
.
(15)某射手射击1次,击中目标的概率是0.9.他连续射击4次,且各次射击是否击中目标相互之间没有影响.有下列结论:
①他第3次击中目标的概率是0.9;
②他恰好击中目标3次的概率是0.93×0.1;
③他至少击中目标1次的概率是1-0.14.
其中正确结论的序号是 (写出所有正确结论的序号).
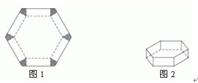
(16)如图1,将边长为1的正六边形铁皮的六个角各 切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器.当这个正六棱柱容器的底面边长为 时,其容积最大.
(1)复数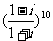 的值是 (A)-1 (B)1 (C)-32 (D)32
的值是 (A)-1 (B)1 (C)-32 (D)32
(2)tan15°+cot15°的值是
(A)2 (B)2+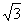 (C)4 (D)
(C)4 (D)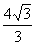
(3)命题p:若a、b∈R,则|a|+|b|>1是|a+b|>1的充分而不必要条件;
命题q:函数y=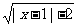 的定义域是(-∞,-1
的定义域是(-∞,-1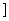 ∪[3,+∞
∪[3,+∞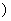 .则
.则
(A)“p或q”为假 (B)“p且q”为真
(C)p真q假 (D)p假q真
(4)已知F1、F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A、B两点,若△ABF2是真正三角形,则这个椭圆的离心率是
(A)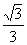 (B)
(B)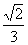 (C)
(C)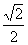 (D)
(D)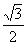
(5)已知m、n是不重合的直线,α、β是不重合的平面,有下列命题:
①若m α,n∥α,则m∥n;
α,n∥α,则m∥n;
②若m∥α,m∥β,则α∥β;
③若α∩β=n,m∥n,则m∥α且m∥β;
④若m⊥α,m⊥β,则α∥β.
其中真命题的个数是
(A)0 (B)1 (C)2 (D)3
(6)某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数为
(A)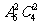 (B)
(B)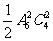 (C)
(C)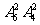 (D)
(D)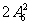
(7)已知函数y=log2x的反函数是y=f-1(x),则函数y= f-1(1-x)的图象是
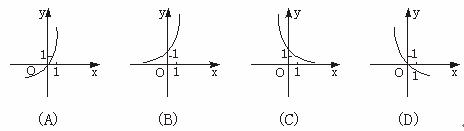
(8)已知a、b是非零向量且满足(a-2b) ⊥a,(b-2a) ⊥b,则a与b的夹角是
(A)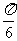 (B)
(B)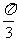 (C)
(C)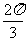 (D)
(D)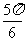
(9)若(1-2x)9展开式的第3项为288,则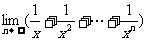 的值是
的值是
(A)2 (B)1 (C)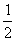 (D)
(D)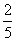
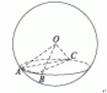
(10)如图,A、B、C是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角是
(A)arcsin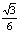 (B)arccos
(B)arccos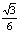 (C)arcsin
(C)arcsin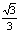 (D)arccos
(D)arccos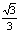
(11)定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-|x-4|,则
(A)f(sin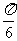 )<f(cos
)<f(cos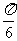 )
(B)f(sin1)>f(cos1)
)
(B)f(sin1)>f(cos1)
(C)f(cos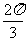 )<f(sin
)<f(sin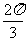 )
(D)f(cos2)>f(sin2)
)
(D)f(cos2)>f(sin2)
(12)如图,B地在A地的正东方向4 km处,C地在B地的北偏东30°方向2 km处,河流的没岸PQ(曲线)上任意一点到A的距离比到B的距离远2 km.现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.经测算,从M到B、M到C修建公路的费用分别是a万元/km、2a万元/km,那么修建这两条公路的总费用最低是
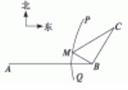
(A)(2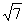 -2)a万元 (B)5a万元
-2)a万元 (B)5a万元
(C)(2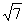 +1) a万元 (D)(2
+1) a万元 (D)(2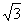 +3) a万元
+3) a万元
第Ⅱ卷
(15)(本小题满分13分)
在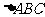 中,
中,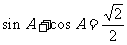 ,
,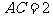 ,
,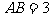 ,求
,求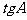 的值和
的值和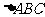 的面积.
的面积.
(16)(本小题满分14分)
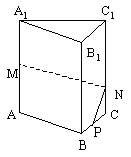
如图,在正三棱柱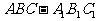 中,AB=3,
中,AB=3,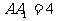 ,M为
,M为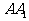 的中点,P是BC上一点,且由P沿棱柱侧面经过棱
的中点,P是BC上一点,且由P沿棱柱侧面经过棱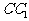 到M的最短路线长为
到M的最短路线长为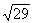 ,设这条最短路线与
,设这条最短路线与 的交点为N,求:
的交点为N,求:
(Ⅰ)该三棱柱的侧面展开图的对角线长;
(II)PC和NC的长;
(III)平面NMP与平面ABC所成二面角(锐角)的大小(用反三角函数表示)
(17)(本小题满分14分)
如图,过抛物线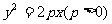 上一定点P(
上一定点P(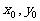 )(
)(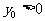 ),作两条直线分别交抛物线于A(
),作两条直线分别交抛物线于A(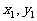 ),B(
),B(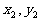 )
)
(I)求该抛物线上纵坐标为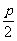 的点到其焦点F的距离
的点到其焦点F的距离
(II)当PA与PB的斜率存在且倾斜角互补时,求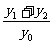 的值,并证明直线AB的斜率是非零常数
的值,并证明直线AB的斜率是非零常数
(18)(本小题满分14分)
函数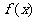 是定义在[0,1]上的增函数,满足
是定义在[0,1]上的增函数,满足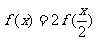 且
且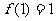 ,在每个区间
,在每个区间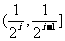 (
(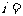 1,2……)上,
1,2……)上,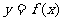 的图象都是斜率为同一常数k的直线的一部分。
的图象都是斜率为同一常数k的直线的一部分。
(I)求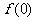 及
及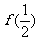 ,
,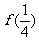 的值,并归纳出
的值,并归纳出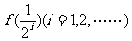 的表达式;
的表达式;
(II)设直线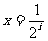 ,
,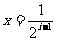 ,x轴及
,x轴及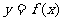 的图象围成的矩形的面积为
的图象围成的矩形的面积为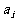 (
(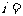 1,2……),记
1,2……),记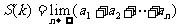 ,求
,求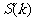 的表达式,并写出其定义域和最小值
的表达式,并写出其定义域和最小值
(19)(本小题满分12分)
某段城铁线路上依次有A、B、C三站,AB=5km,BC=3km,在列车运行时刻表上,规定列车8时整从A站发车,8时07分到达B站并停车1分钟,8时12分到达C站.在实际运行中,假设列车从A站正点发车,在B站停留1分钟,并在行驶时以同一速度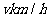 匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
(I)分别写出列车在B、C两站的运行误差;
(II)若要求列车在B,C两站的运行误差之和不超过2分钟,求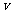 的取值范围.
的取值范围.
(20)(本小题满分13分)
给定有限个正数满足条件T:每个数都不大于50且总和L=1275.现将这些数按下列要求进行分组,每组数之和不大于150且分组的步骤是:
首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差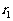 与所有可能的其他选择相比是最小的,
与所有可能的其他选择相比是最小的,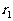 称为第一组余差;
称为第一组余差;
然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,这时的余差为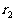 ;如此继续构成第三组(余差为
;如此继续构成第三组(余差为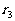 )、第四组(余差为
)、第四组(余差为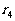 )、……,直至第N组(余差为
)、……,直至第N组(余差为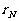 )把这些数全部分完为止.
)把这些数全部分完为止.
(I)判断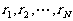 的大小关系,并指出除第N组外的每组至少含有几个数;
的大小关系,并指出除第N组外的每组至少含有几个数;
(II)当构成第n(n<N)组后,指出余下的每个数与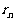 的大小关系,并证明
的大小关系,并证明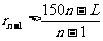 ;
;
(III)对任何满足条件T的有限个正数,证明: .
.
(9) 函数 的最小正周期是___________.
的最小正周期是___________.
(10)方程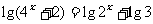 的解是___________________ .
的解是___________________ .
(11)某地球仪上北纬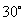 纬线的长度为
纬线的长度为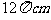 ,该地球仪的半径是__________cm,表面积是______________cm2.
,该地球仪的半径是__________cm,表面积是______________cm2.
(12)曲线C: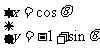 (
(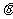 为参数)的普通方程是__________,如果曲线C与直线
为参数)的普通方程是__________,如果曲线C与直线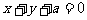 有公共点,那么实数a的取值范围是_______________.
有公共点,那么实数a的取值范围是_______________.
(13)在函数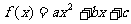 中,若a,b,c成等比数列且
中,若a,b,c成等比数列且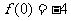 ,则
,则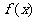 有最______________值(填“大”或“小”),且该值为______________.
有最______________值(填“大”或“小”),且该值为______________.
(14)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.
已知数列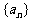 是等和数列,且
是等和数列,且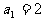 ,公和为5,那么
,公和为5,那么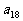 的值为_____________
的值为_____________
这个数列的前n项和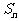 的计算公式为________________ .
的计算公式为________________ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com