
(11)复数复数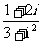 的值是_________.
的值是_________.
(12)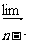
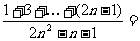 _________.
_________.
(13)已知
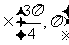 ,sin(
,sin( )=-
)=-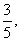 sin
sin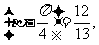 则os
则os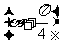 =________.
=________.
(14)在数列{an}中,若a1=1,an+1=2an+3 (n≥1),则该数列的通项an=_________.
(15)设a>0,n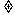 1,函数f(x)=alg(x2-2n+1) 有最大值.则不等式logn(x2-5x+7)
>0的解集为_______.
1,函数f(x)=alg(x2-2n+1) 有最大值.则不等式logn(x2-5x+7)
>0的解集为_______.
(16)已知变量x,y满足约束条件1≤x+y≤4,-2≤x-y≤2.若目标函数z=ax+y(其中a>0)仅在点(3,1)处取得最大值,则a的取值范围为___________.
第二卷
(15)若S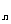 是公差不为0的等差数列
是公差不为0的等差数列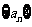 的前n项和,且
的前n项和,且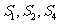 成等比数列。
成等比数列。
(Ⅰ)求数列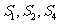 的公比。
的公比。
(Ⅱ)若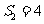 ,求
,求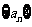 的通项公式.
的通项公式.
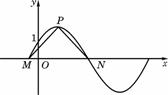
16)如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤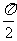 )的图像与y轴交于点(0,1).
)的图像与y轴交于点(0,1).
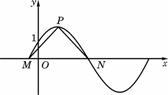
(Ⅰ)求φ的值;
(Ⅱ)设P是图像上的最高点,M、N是图像与x轴的交点,求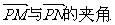
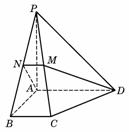
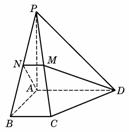
(17)如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
(Ⅰ)求证:PB⊥DM;
(Ⅱ)求BD与平面ADMN所成的角。
(18)甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;乙袋装有2个红球,n个白球.现从甲,乙两袋中各任取2个球.
(Ⅰ)若n=3,求取到的4个球全是红球的概率;
(Ⅱ)若取到的4个球中至少有2个红球的概率为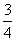 ,求n.
,求n.
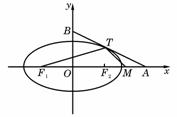
(19)如图,椭圆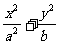 =1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=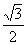 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)设F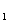 、F
、F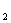 分别为椭圆的左、右焦点,求证:
分别为椭圆的左、右焦点,求证: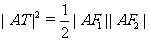 。
。
(20)设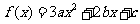 ,
,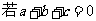 ,f(0)f(1)>0,求证:
,f(0)f(1)>0,求证:
(Ⅰ)方程 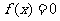 有实根。
有实根。
(Ⅱ) -2<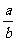 <-1;
<-1;
(III)设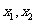 是方程f(x)=0的两个实根,则.
是方程f(x)=0的两个实根,则.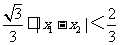
(11)不等式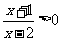 的解集是 。.
的解集是 。.
(12)函数y=2sinxcosx-1,x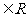 的值域是
的值域是
(13)双曲线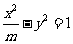 上的点到左焦点的距离与到左准线的距离的比是3,则
上的点到左焦点的距离与到左准线的距离的比是3,则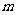 等于
等于
(14)如图,正四面体ABCD的棱长为1,平面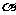 过棱AB,且CD∥α,则正四面体上的所有点在平面α内的射影构成的图形面积是 .
过棱AB,且CD∥α,则正四面体上的所有点在平面α内的射影构成的图形面积是 . 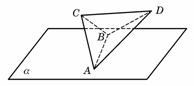
(1)设集合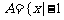 ≤x≤2},B={x|0≤x≤4},则A∩B=
≤x≤2},B={x|0≤x≤4},则A∩B=
(A)[0,2] (B)[1,2] (C)[0,4] (D)[1,4]
(2)在二项式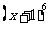 的展开式中,含
的展开式中,含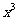 的项的系数是
的项的系数是
(A)15 (B)20 (C)30 (D)40
(3)抛物线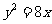 的准线方程是
的准线方程是
(A) 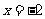 (B)
(B) 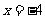 (C)
(C) 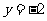 (D)
(D)
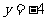
(4)已知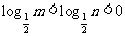 ,则
,则
(A) n<m < 1 (B) m<n< 1 (C) 1< m<n (D) 1 <n<m
(5)设向量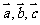 满足
满足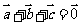 ,
,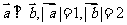 ,则
,则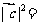
(A)1 (B)2 (C)4 (D)5
(6)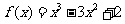 在区间
在区间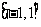 上的最大值是
上的最大值是
(A)-2 (B)0 (C)2 (D)4
(7)“a>0,b>0”是“ab>0”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不允分也不必要条件
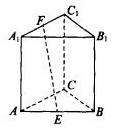
(8)如图,正三棱柱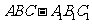 的各棱长都2,E,F分别是
的各棱长都2,E,F分别是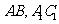 的中点,则EF的长是
的中点,则EF的长是
(A)2
(B)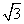 (C)
(C) 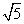 (D)
(D)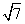
(9) 在平面直角坐标系中,不等式组 表示的平面区域的面积是
表示的平面区域的面积是
(A)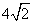 (B)4
(C)
(B)4
(C) 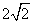 (D)2
(D)2
(10)对a,b R,记max{a,b}=
R,记max{a,b}=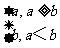 ,函数f(x)=max{|x+1|,|x-2|}(x
,函数f(x)=max{|x+1|,|x-2|}(x R)的最小值是
R)的最小值是
(A)0
(B)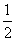 (C
(C 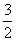 (D)3
(D)3
第Ⅱ卷
(15)如图,函数y=2sin(πxφ),x∈R,(其中0≤φ≤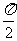 )的图像与y轴交于点(0,1).
)的图像与y轴交于点(0,1).
(Ⅰ)求φ的值;
(Ⅱ)设P是图像上的最高点,M、N是图像与x轴的交点,求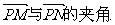
(16)设f(x)=3ax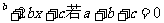 ,f(0)>0,f(1)>0,求证:
,f(0)>0,f(1)>0,求证:
(Ⅰ)a>0且-2<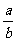 <-1;
<-1;
(Ⅱ)方程f(x)=0在(0,1)内有两个实根.
(17)如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
(Ⅰ)求证:PB⊥DM;
(Ⅱ)求CD与平面ADMN所成的角
(18)甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;乙袋装有2个红球,n个白球.两甲,乙两袋中各任取2个球.
(Ⅰ)若n=3,求取到的4个球全是红球的概率;
(Ⅱ)若取到的4个球中至少有2个红球的概率为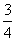 ,求n.
,求n.
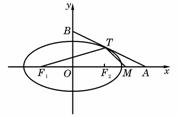
(19)如图,椭圆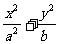 =1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=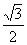 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)设F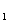 、F
、F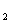 分别为椭圆的左、右焦点,M为线段AF
分别为椭圆的左、右焦点,M为线段AF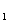 的中点,求证:∠ATM=∠AF
的中点,求证:∠ATM=∠AF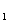 T.
T.
(20)已知函数f(x)=x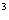 + x
+ x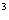 ,数列|x
,数列|x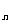 |(x
|(x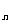 >0)的第一项x
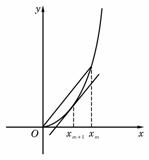
>0)的第一项x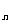 =1,以后各项按如下方式取定:曲线x=f(x)在
=1,以后各项按如下方式取定:曲线x=f(x)在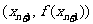 处的切线与经过(0,0)和(x
处的切线与经过(0,0)和(x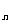 ,f
(x
,f
(x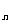 ))两点的直线平行(如图)
))两点的直线平行(如图)
 .
.
求证:当n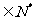 时,
时,
(Ⅰ)x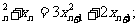
(Ⅱ)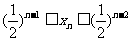
(11)设S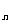 为等差数列a,的前n项和,若S
为等差数列a,的前n项和,若S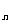 -10,
S
-10,
S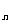 =-5,则公差为 (用数字作答).
=-5,则公差为 (用数字作答).
(12)对a,b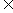 R,记max|a,b|=
R,记max|a,b|=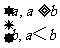 函数f(x)=max||x+1|,|x-2||(x
函数f(x)=max||x+1|,|x-2||(x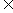 R)的最小值是 .
R)的最小值是 .
(13)设向量a、b、c 满足a+b+c=0,(a-b)⊥c,a⊥b,若|a|=1,则|a|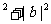 +|c|
+|c|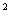 的值是
的值是
(14)正四面体ABCD的棱长为1,棱AB∥平面α,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是 . 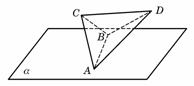
(1) 设集合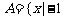 ≤x≤2},B={x|0≤x≤4},则A∩B=
≤x≤2},B={x|0≤x≤4},则A∩B=
(A)[0,2] (B)[1,2] (C)[0,4] (D)[1,4]
(2) 已知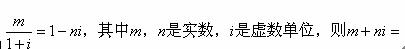
(A)1+2i (B) 1-2i (C)2+i (D)2-I
(3)已知0<a<1,log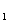 m<log
m<log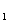 n<0,则
n<0,则
(A)1<n<m (B) 1<m<n (C)m<n<1 (D) n<m<1
(3) 在平面直角坐标系中,不等式组 表示的平面区域的面积是
表示的平面区域的面积是
(A)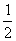 (B)
(B)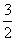 (C)
(C)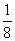 (D)
(D)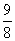
(6)函数y=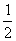 sin2+4sin
sin2+4sin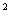 x, (x
x, (x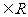 )的值域是
)的值域是
(A)[-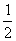 ,
,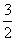 ]
(B)[-
]
(B)[-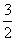 ,
,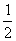 ]
]
(C)[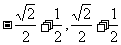 ]
(D)[
]
(D)[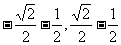 ]
]
(7)“a>b>c”是“ab<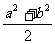 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不允分也不必要条件
(8)若多项式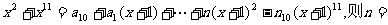
(A)9 (B)10 (C)-9 (D)-10
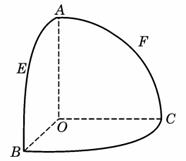
(9)如图,O是半径为l的球心,点A、B、C在球面上,OA、OB、OC两两垂直,E、F分别是大圆弧AB与AC的中点,则点E、F在该球面上的球面距离是
(A)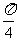 (B)
(B)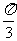 (C)
(C)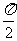 (D)
(D)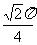
(10)函数f:|1,2,3| |1,2,3|满足f(f(x))= f(x),则这样的函数个数共有
|1,2,3|满足f(f(x))= f(x),则这样的函数个数共有
(A)1个 (B)4个 (C)8个 (D)10个
第Ⅱ卷
22.(本小题满分12分)
已知两定点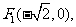
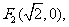 满足条件
满足条件 的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点。
的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点。
(Ⅰ)求k的取值范围;
(Ⅱ)如果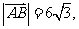 且曲线E上存在点C,使
且曲线E上存在点C,使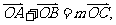 求
求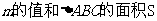 。
。
21.(本小题满分14分)
已知函数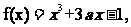
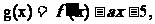 其中
其中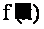 是的f(x)的导函数。
是的f(x)的导函数。
(Ⅰ)对满足 的一切
的一切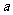 的值, 都有
的值, 都有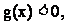 求实数x的取值范围;
求实数x的取值范围;
(Ⅱ)设 ,当实数m在什么范围内变化时,函数y=f(x)的图像与直线y=3只有一个公共点。
,当实数m在什么范围内变化时,函数y=f(x)的图像与直线y=3只有一个公共点。
20.(本小题满分12分)
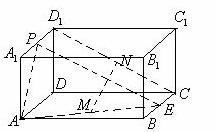
如图,长方体ABCD-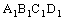 中,E、P分别是BC、
中,E、P分别是BC、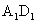 的中点, M、N分别是AE、
的中点, M、N分别是AE、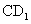 的中点,
的中点, 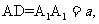
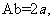
(Ⅰ)求证: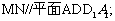 ;
;
(Ⅱ)求二面角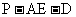 的大小;
的大小;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com