
3.设数列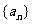 是等差数列,且
是等差数列,且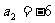 ,
,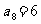 ,
,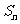 是数列
是数列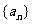 的前
的前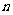 项和,则
项和,则
(A)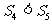 (B)
(B)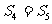 (C)
(C)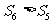 (D)
(D)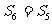
2.函数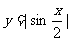 的最小正周期是
的最小正周期是
(A)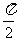 (B)
(B) (C)
(C)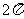 (D)
(D)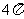
1.设集合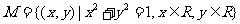 ,
,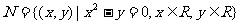 ,则集合
,则集合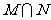 中元素的个数为
中元素的个数为
(A)1 (B)2 (C)3 (D)4
(17)(本小题满分12分)
解方程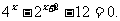
(18) (本小题满分12分)
已知α为锐角,且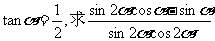 的值.
的值.
(19) (本上题满分12分)
设数列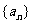 是公差不为零的等差数列,Sn是数列
是公差不为零的等差数列,Sn是数列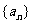 的前n项和,且
的前n项和,且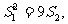
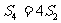 ,求数列
,求数列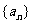 的通项公式.
的通项公式.
20.(本小题满分12分)
某村计划建造一个室内面积为800m2的矩形蔬菜温室,在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地。当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
(21) (本小题满分12分)
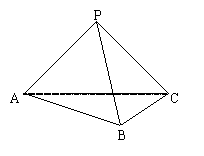
三棱锥P-ABC中,侧面PAC与底面ABC垂直,PA=PB=PC=3.
(1) 求证AB⊥BC;
(2)
如果AB=BC=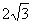 ,求侧面PBC与侧面PAC所成二面角的大小.
,求侧面PBC与侧面PAC所成二面角的大小.
(22)(本小题满分14分)
设椭圆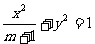 的两个焦点是
的两个焦点是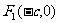 与
与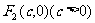 ,且椭圆上存在点P,使得直线PF2与直线PF2垂直.
,且椭圆上存在点P,使得直线PF2与直线PF2垂直.
(1)求实数m的取值范围;
(2)设L是相应于焦点F2的准线,直线PF2与L相交于点Q. 若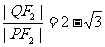 ,
,
求直线PF2的方程.
(13) 函数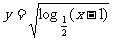 的定义域是
.
的定义域是
.
(14) 用平面α截半径为R的球,如果球心到平面α的距离为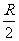 ,那么截得小圆的面积与球
,那么截得小圆的面积与球
的表面积的比值为 .
(15) 函数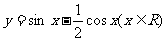 的最大值为
.
的最大值为
.
(16) 设P为圆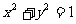 上的动点,则点P到直线
上的动点,则点P到直线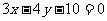 的距离的最小值为
的距离的最小值为
.
(1)设集合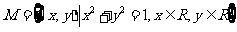 ,
,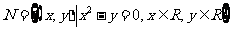 , 则集合
, 则集合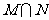 中元素的个数为( )
中元素的个数为( )
A.1 B.2 C.3 D.4
(2)函数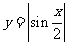 的最小正周期是( )
的最小正周期是( )
A.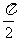 B.
B.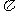 C.
C.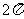 D.
D.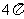
(3) 记函数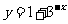 的反函数为
的反函数为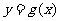 ,则
,则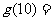 ( )
( )
A. 2
B.  C. 3 D.
C. 3 D. 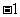
(4) 等比数列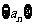 中,
中,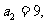
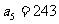 ,则
,则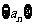 的前4项和为( )
的前4项和为( )
A. 81 B. 120 C.168 D. 192
(5) 圆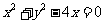 在点
在点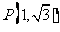 处的切线方程是( )
处的切线方程是( )
A. 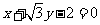 B.
B. 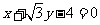
C. 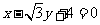 D.
D. 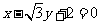
(6) 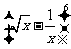 展开式中的常数项为( )
展开式中的常数项为( )
A. 15 B. 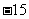 C.
C.  20 D.
20 D. 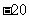
(7) 设复数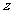 的幅角的主值为
的幅角的主值为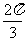 ,虚部为
,虚部为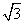 ,则
,则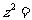 ( )
( )
A. 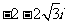 B.
B. 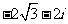
C. 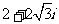 D.
D. 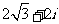
(8) 设双曲线的焦点在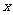 轴上,两条渐近线为
轴上,两条渐近线为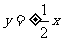 ,则双曲线的离心率
,则双曲线的离心率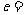 ( )
( )
A. 5 B. 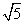 C.
C. 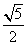 D.
D. 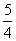
(9) 不等式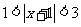 的解集为( )
的解集为( )
A. 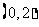 B.
B. 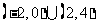
C. 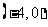 D.
D. 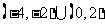
(10) 正三棱锥的底面边长为2,侧面均为直角三角形,则此三棱锥的体积为( )
A. 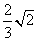 B.
B. 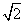 C.
C. 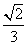 D.
D. 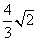
(11) 在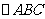 中,
中,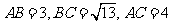 ,则边
,则边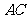 上的高为( )
上的高为( )
A. 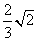 B.
B. 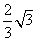 C.
C. 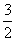 D.
D.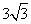
(12) 4名教师分配到3所中学任教,每所中学至少1名教师,则不同的分配方案共有( )
A. 12 种 B. 24 种 C 36 种 D. 48 种
第Ⅱ卷
22.(本小题满分12分)
已知函数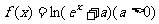 .
.
(1)求函数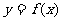 的反函数
的反函数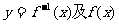 的导数
的导数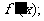
(2)假设对任意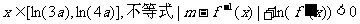 成立,求实
成立,求实
数m的取值范围.
21.(本小题满分14分)
已知函数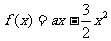 的最大值不大于
的最大值不大于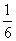 ,又当
,又当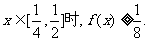
(1)求a的值;
(2)设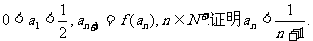
20.(本小题满分12分)
甲方是一农场,乙方是一工厂. 由于乙方生产须占用甲方的资源,因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润x(元)与年产量t(吨)满足函数关系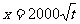 .若乙方每生产一吨产品必须赔付甲方s元(以下称s为赔付价格),
.若乙方每生产一吨产品必须赔付甲方s元(以下称s为赔付价格),
(1)将乙方的年利润w(元)表示为年产量t(吨)的函数,并求出乙方获得最大利润
的年产量;
(2)甲方每年受乙方生产影响的经济损失金额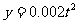 (元),在乙方按照获得最大
(元),在乙方按照获得最大
利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的
赔付价格s是多少?
19.(本小题满分12分)
设椭圆方程为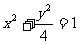 ,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足
,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足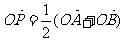 ,点N的坐标为
,点N的坐标为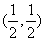 ,当l绕点M旋转时,求:
,当l绕点M旋转时,求:
(1)动点P的轨迹方程;
(2)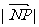 的最小值与最大值.
的最小值与最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com