
3.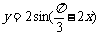 单调增区间为 ( )
单调增区间为 ( )
A.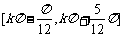 B.
B.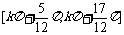
C.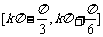 D.
D.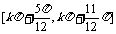
2.有下列四个命题,其中真命题有:
①“若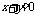 ,则
,则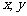 互为相反数”的逆命题;
互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若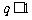 ,则
,则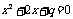 有实根”的逆命题;
有实根”的逆命题;
④“不等边三角形的三个内角相等”的逆否命题; ( )
A.①② B.②③ C.①③ D.③④
1.设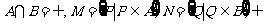 为空集,则: ( )
为空集,则: ( )
A.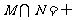 B.
B.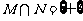 C.
C.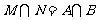 D.
D.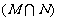
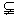
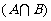
22.(本题满分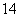 分)
分)
已知函数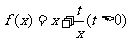 和点
和点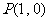 ,过点
,过点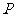 作曲线
作曲线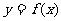 的两条切线
的两条切线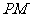 、
、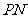 ,切点分别为
,切点分别为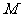 、
、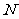 .
.
(Ⅰ)设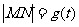 ,试求函数
,试求函数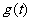 的表达式;
的表达式;
(Ⅱ)是否存在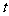 ,使得
,使得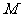 、
、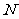 与
与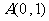 三点共线.若存在,求出
三点共线.若存在,求出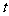 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数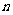 ,在区间
,在区间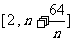 内总存在
内总存在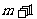 个实数
个实数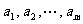 ,
,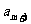 ,使得不等式
,使得不等式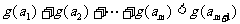 成立,求
成立,求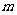 的最大值.
的最大值.
20、函数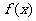 的定义域为R,且对任意
的定义域为R,且对任意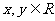 ,有
,有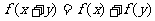 ,且当
,且当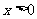 时,
时,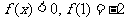 。(12分)
。(12分)
(1) 证明: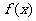 是奇函数;
是奇函数;
(2) 证明: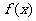 是R上的减函数;
是R上的减函数;
(3) 求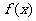 在区间
在区间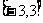 上的最大、最小值
上的最大、最小值
21(本小题满分12分)
一束光线从点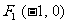 出发,经直线
出发,经直线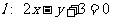 上一点
上一点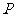 反射后,恰好穿过点
反射后,恰好穿过点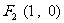 .
.
(Ⅰ)求点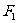 关于直线
关于直线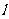 的对称点
的对称点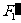 的坐标;
的坐标;
(Ⅱ)求以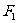 、
、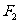 为焦点且过点
为焦点且过点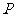 的椭圆
的椭圆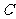 的方程;
的方程;
(Ⅲ)设直线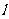 与椭圆
与椭圆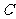 的两条准线分别交于
的两条准线分别交于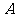 、
、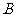 两点,点
两点,点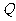 为线段
为线段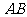 上的动点,求点
上的动点,求点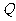 到
到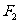 的距离与到椭圆
的距离与到椭圆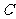 右准线的距离之比的最小值,并求取得最小值时点
右准线的距离之比的最小值,并求取得最小值时点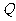 的坐标.
的坐标.
19.(本题满分12分)
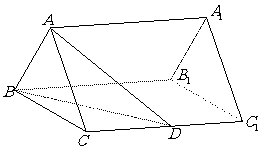 如图,已知正三棱柱
如图,已知正三棱柱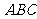 -
-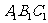 的底面边长是
的底面边长是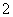 ,
,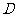 是侧棱
是侧棱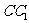 的中点,直线
的中点,直线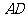 与侧面
与侧面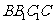 所成的角为
所成的角为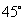 .
.
(Ⅰ)求此正三棱柱的侧棱长;
(Ⅱ) 求二面角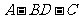 的大小;
的大小;
(Ⅲ)求点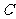 到平面
到平面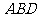 的距离.
的距离.
17、已知两个向量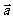 、
、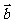 不共线,且
不共线,且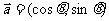 ,
,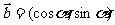 ,若
,若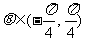 ,
,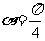 ,且
,且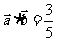 ,求
,求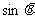 的值。(12分)
的值。(12分)
18(本题满分12分)
在一个盒子中,放有标号分别为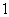 ,
,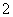 ,
,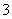 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为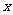 、
、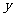 ,记
,记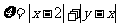 .(12分)
.(12分)
(Ⅰ)求随机变量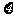 的最大值,并求事件“
的最大值,并求事件“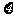 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量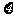 的分布列和数学期望.
的分布列和数学期望.
14.已知i, j为互相垂直的单位向量,a = i – 2j, b = i + λj,且a与b的夹角为锐角,则实数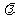 的取值范围是 .
的取值范围是 .
15已知函数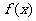 ,对任意实数
,对任意实数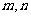 满足
满足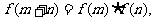 且
且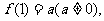
则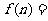
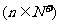 .
.
16符号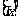 表示不超过
表示不超过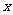 的最大整数,如
的最大整数,如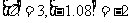 ,定义函数
,定义函数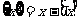 ,
,
那么下列命题中正确的序号是 .
(1)函数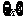 的定义域为R,值域为
的定义域为R,值域为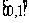 ; (2)方程
; (2)方程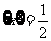 ,有无数解;
,有无数解;
(3)函数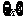 是周期函数;
(4)函数
是周期函数;
(4)函数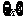 是增函数.
是增函数.
13.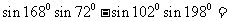 .
.
12.(理)在y=2x,y=x2,y=cos2x这三个函数中,当0<x1<x2<1时,使f(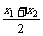 )<
)<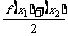 恒成立的函数的个数是 ( ) C
恒成立的函数的个数是 ( ) C
A.0 B.1 C.2 D.3
 |
|||
|
|||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com