
2.设复数: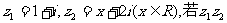 为实数,则x= ( )
为实数,则x= ( )
A.-2 B.-1 C.1 D.2
1.设集合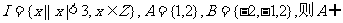 (CIB)=( )
(CIB)=( )
A.{1} B.{1,2} C.{2} D.{0,1,2}
(19)(本小题满分12分)
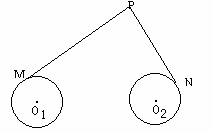
如图,圆O1与圆O2的半径都等于1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得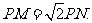 试建立平面直角坐标系,并求动点P的轨迹方程.
试建立平面直角坐标系,并求动点P的轨迹方程.
(20)(本小题满分12分,每小问满分4分)
甲、乙两人各射击1次,击中目标的概率分别是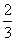 和
和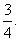 假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
(Ⅰ)求甲射击4次,至少有1次未击中目标的概率;
(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(Ⅲ)假设某人连续2次未击中目标,则中止其射击.问:乙恰好射击5次后,被中止射击的概率是多少?
(21)(本小题满分14分,第一小问满分6分,第二、第三小问满分各4分)
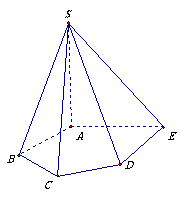
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=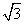 ,
,
∠BAE=∠BCD=∠CDE=120°.
(Ⅰ)求异面直线CD与SB所成的角(用反三角函数值表示);
(Ⅱ)证明BC⊥平面SAB;
(Ⅲ)用反三角函数值表示二面角B-SC-D的大小(本小问不必写出解答过程)
(22)(本小题满分14分,第一小问满分4分,第二小问满分10分)已知a∈R,函数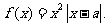
(Ⅰ)当a=2时,求使f(x)=x成立的x的集合;
(Ⅱ)求函数y=f (x)在区间[1,2]上的最小值.
(23)(本小题满分14分,第一小问满分2分,第二、第三小问满分各6分)设数列{an}的前n项和为Sn,已知a1=1,a2=6,a3=11,且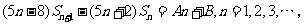 其中A,B为常数.
其中A,B为常数.
(Ⅰ)求A与B的值;
(Ⅱ)证明数列{an}为等差数列;
(Ⅲ)证明不等式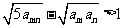 对任何正整数m、n都成立.
对任何正整数m、n都成立.
(13)命题“若a>b,则2a>2b-1”的否命题为 .
(14)曲线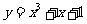 在点(1,3)处的切线方程是
.
在点(1,3)处的切线方程是
.
(15)函数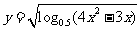 的定义域为
.
的定义域为
.
(16)若3a=0.618,a∈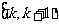 ,k∈Z,则k= .
,k∈Z,则k= .
(17)已知a,b为常数,若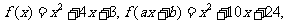 则
则 .
.
(18)在△ABC中,O为中线AM上的一个动点,若AM=2,则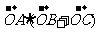 的最小值是
.
的最小值是
.
(1)设集合A={1,2},B={1,2,3},C={2,3,4},则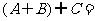
(A){1,2,3} (B){1,2,4} (C){2,3,4} (D){1,2,3,4}
(2)函数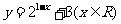 的反函数的解析表达式为
的反函数的解析表达式为
(A)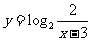 (B)
(B)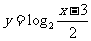
(C)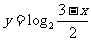 (D)
(D)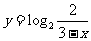
(3)在各项都为正数的等比数列{an}中,首项a1=3,前三项和为21,则a3+a4+a5=
(A)33 (B)72 (C)84 (D)189
(4)在正三棱柱中ABC-A1B1C1中,若AB=2,AA1=1,则点A到平面A1BC的距离为
(A)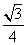 (B)
(B)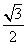 (C)
(C)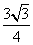 (D)
(D)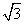
(5)△ABC中,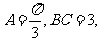 则△ABC的周长为
则△ABC的周长为
(A)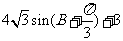 (B)
(B)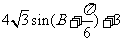
(C)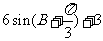 (D)
(D)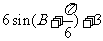
(6)抛物线y=4x2上的一点M到焦点的距离为1,则点M的纵坐标是
(A)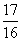 (B)
(B)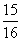 (C)
(C)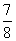 (D)0
(D)0
(7)在一次歌手大奖赛上,七位评委为歌手打出的分数如下:
9.4 8.4 9.4 9.9 9.6 9.4 9.7
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为
(A)9.4, 0.484 (B)9.4, 0.016 (C)9.5, 0.04 (D)9.5, 0.016
(8)设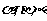 为两两不重合的平面,l、m、n为两两不重合的直线,给出下列四个命题:
为两两不重合的平面,l、m、n为两两不重合的直线,给出下列四个命题:
①若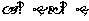 则
则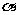 ∥
∥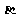 ;
;
②若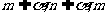 ∥
∥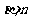 ∥
∥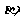 则
则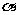 ∥
∥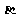 ;
;
③若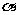 ∥
∥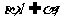 则
则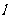 ∥
∥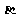 ;
;
④若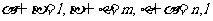 ∥
∥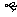 则m∥n.
则m∥n.
其中真命题的个数是
(A)1 (B)2 (C)3 (D)4
(9)设k=1,2,3,4,5,则(x+2)5的展开式中xk的系数不可能是
(A)10 (B)40 (C)50 (D)80
(10)若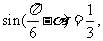 则
则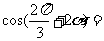
(A)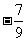 (B)
(B)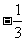 (C)
(C)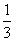 (D)
(D)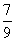
(11)点P(-3,1)在椭圆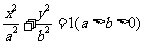 的左准线上.过点P且方向为a=(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为
的左准线上.过点P且方向为a=(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为
(A)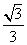 (B)
(B)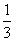 (C)
(C)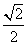 (D)
(D)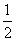
(12)四棱锥的8条棱代表8种不同的化工产品,有公共点的两条棱代表的化工产品放在同一仓库是危险的,没有公共顶点的两条棱所代表的化工产品放在同一仓库是安全的,现打算用编号为①、②、③、④的4个仓库存放这8种化工产品,那么安全存放的不同方法种数为
(A)96 (B)48 (C)24 (D)0
第二卷(非选择题共90分)
22.(本小题满分14分)
已知不等式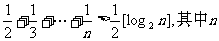 为大于2的整数,
为大于2的整数,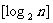 表示不超过
表示不超过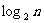 的最大整数. 设数列
的最大整数. 设数列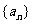 的各项为正,且满足
的各项为正,且满足
 .
.
(Ⅰ)证明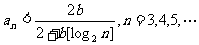 ;
;
(Ⅱ)猜测数列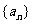 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);
(Ⅲ)试确定一个正整数N,使得当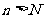 时,对任意b>0,都有
时,对任意b>0,都有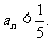
21.(本小题满分12分)
设A、B是椭圆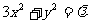 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(Ⅰ)确定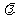 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的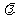 ,使得A、B、C、D四点在同一个圆上?并说明理由.
,使得A、B、C、D四点在同一个圆上?并说明理由.
20.(本小题满分12分)
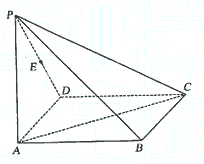
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=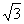 ,
,
BC=1,PA=2,E为PD的中点.
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离.
19.(本小题满分12分)
某地最近出台一项机动车驾照考试规定;每位考试者一年之内最多有4次参加考试的机会,一旦某次考试通过,使可领取驾照,不再参加以后的考试,否则就一直考到第4次为止。如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9,求在一年内李明参加驾照考试次数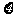 的分布列和
的分布列和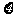 的期望,并求李明在一年内领到驾照的概率.
的期望,并求李明在一年内领到驾照的概率.
18.(本小题满分12分)
在△ABC中,已知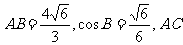 边上的中线BD=
边上的中线BD=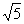 ,求sinA的值.
,求sinA的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com