
(1)函数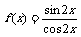 的最小正周期是
的最小正周期是
(A)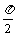 (B) (C)2 (D)4
(B) (C)2 (D)4
(2)圆(x-1)2+y2=1的圆心到直线y=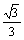 x的距离是
x的距离是
(A)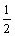 (B)
(B)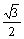 (C)1 (D)
(C)1 (D)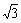
(3)不等式(1+x)(1-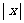 )>0的解集是
)>0的解集是
(A){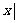 0≤x≤1} (B){
0≤x≤1} (B){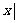 x<0 且x≠-1}
x<0 且x≠-1}
(C){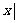 -1<x<1} (D){
-1<x<1} (D){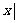 x<1且x≠-1}
x<1且x≠-1}
(4)在(0,2)内,使sinx>cosx成立的x取值范围为
(A)(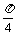 ,
,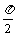 )∪(,
)∪(,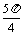 ) (B)(
) (B)(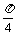 ,)
,)
(C)(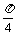 ,
,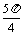 ) (D)(
) (D)(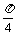 ,)∪(
,)∪(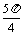 ,
,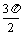 )
)
(5)设集合M=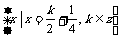 ,N=
,N=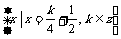 ,则
,则
(A)M=N (B)MN (C)MN (D)M∩N=
(6)一个圆锥和一个半球有公共底面,如果圆锥的体积恰好与半球的体积相等,那么,这个圆锥轴截面顶角的余弦值是
(A)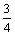 (B)
(B)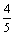 (C)
(C)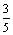 (D)-
(D)-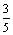
(7)函数f(x)=x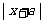 +b是奇函数的充要条件是
+b是奇函数的充要条件是
(A)ab=0 (B)a+b=0 (C)a=b (D)a2+b2=0
(8)已知0<x<y<a<1则有
(A)loga(xy)<0 (B)0<loga(xy)<1
(C)1<loga(xy)<2 (D)loga(xy)>2
(9)函数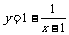
(A)在(-1,+∞)内单调递增 (B)在(-1,+∞)内单调递减
(C)在(1,+∞)内单调递增 (D)在(1,+∞)内单调递减
(10)极坐标方程=com与 com=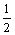 的图形是
的图形是

(11)从正方体的6个面中选取3个面,其中有2个面不相邻的选法共有
(A)8种 (B)12种 (C)16种 (D)20种
(12)据2002年3月5日九届人大五次会议(政府工作报告):“2001年国内生产总值达到95933亿元,比上年增长7.3%.”如果“十五”期间(2001-2005年)每年的国内生产总值都按此年增长率增长,那么到“十五”末我国国内年生产总值为
(A)115000亿 (B)120000亿 (C)127000亿 (D)135000亿
第II 卷
(17)(本小题满分12分)
已知等差数列前三项为a,4,3a,前n项的和为Sn,Sk=2550.
(Ⅰ)求a及k的值;
(Ⅱ)求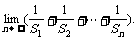
(18)(本小题满分12分)
设计一幅宣传画,要求画面面积为4840cm2,画面的宽与高的比为λ(λ<1),画面的上、下各有8 cm空白,左、右各有5 cm空白。怎样确定画面的高与宽尺寸,能使宣传画所用纸张的面积最小?
(19)(本小题满分12分)
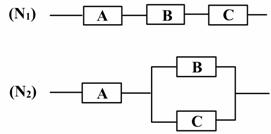
如图,用A、B、C三类不同的元件连接或两个系统N1、N2, 当元件A、B、C都正常工作时,系统N1、N2正常工作; 当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作,已知元件A、B、C正常工作的概率依次为0.80,0.90,0.90。分别求系统N1、N2正常工作的概率P1、P2
注意:考生在(20甲)、(20乙)两题中选一题作答,如果两题都答,只以(20甲)计分。
(20甲)(本小题满分12分)
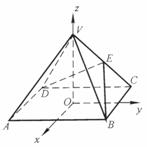
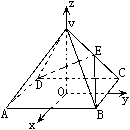
如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.
Ⅰ.求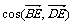 ;
;
Ⅱ.记面BCV为α,面DCV为β,若∠BED是二面角α―VC―β的平面角,求cos∠BED的值。
(20乙)(本小题满分12分)
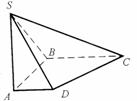
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC,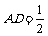 .
.
(Ⅰ)求四棱锥S-ABCD的体积;
(Ⅱ)求面SCD与面SBA所成的二面角的正切值。
(21)(本小题满分12分) 已知函数f(x)=x2 -3ax2+2bx在点x=1处有极小值-1。试确定a、b的值,并求出f(x)的单调区间。
(22)(本小题满分14分)
设0<θ<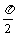 ,曲线x2sinθ+y2cosθ=1和x2cosθ-y2sinθ=1有4个不同的交点.
,曲线x2sinθ+y2cosθ=1和x2cosθ-y2sinθ=1有4个不同的交点.
(Ⅰ)求θ的取值的范围;
(Ⅱ)证明这4个交点共圆,并求圆半径的取值范围。
(13)定义在R上的函数f (x)=sinx+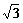 cosx是最大值是 。
cosx是最大值是 。
(14)一个工厂有若干个车间,今采用分层抽样方法从全厂某天的2048件产品中抽取一个容量为128的样本进行质量检查。若一车间这一天生产256件产品,则从该车间抽取的产品件数为 。
(15)在空间中,
①若四点不共面,则这四点中任何三点都不共线
②若两条直线没有公共点,则这两条直线是异面直线
以上两个命题中,逆命题为真命题的是 。(把符合要求的命题序号都填上)
(16)若{an}是公比为q的等比数列,Sn是它的前n项和。若{Sn}是等差数列,则q= 。
(1)设A={x|x2-x=0},B={x|x2+x=0},则A∩B等于
(A)0 (B){0} (C)Ø (D){-1,0,1}
(2)若Sn是数列{an}的前n项和,且Sn=n2,则{an}是
(A)等比数列,但不是等差数列
(B)等差数列,但不是等比数列
(C)等差数列,而且也是等比数列
(D)既非等比数列又非等差数列
(3)过点A(1,- 1)、B(-1,1)且圆心在直线x+y-2=0上的圆的方程是
(A)(x-1)2+(y-1)2=4 (B)(x+3)2+(y-1)2=4
1)、B(-1,1)且圆心在直线x+y-2=0上的圆的方程是
(A)(x-1)2+(y-1)2=4 (B)(x+3)2+(y-1)2=4
(C)(x-3)2+(y+1)2=4 (D)(x+1)2+(y+1)2=4
(4)若定义在区间(-1,0)内的函数f(x)=log2a(x+1)满足f(x)>0,则α的取值范围是
(A)(0,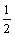 ) (B)(0,
) (B)(0,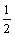 )
)
(C)(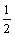 ,+∞) (D)(0,+∞)
,+∞) (D)(0,+∞)
(5)若向量a=(3,2),b=(0,-1),则向量2b-a的坐标是
(A)(3,-4) (B)(-3,4)
(C)(3,4) (D)(-3,-4)
(6)设A、B是x轴上的两点,点P的横坐标为2且|PA|=|PB|.若直线PA的方程为x-y+1=0,则直线PB的方程是
(A)x+y-5=0 (B)2x-y-1=0
(C)2y-x-4=0 (D)2x+y-7=0
(7)若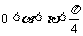 ,sinα+cosα=a,sinβ+cosβ=b,则
(A)ab<1 (B)a>b (C)a<b (D)ab>2
,sinα+cosα=a,sinβ+cosβ=b,则
(A)ab<1 (B)a>b (C)a<b (D)ab>2
(8)若椭圆经过原点,且焦点为F1(1,0),F2(3,0),则其离心率为
(A)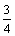 (B)
(B)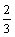 (C)
(C)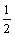 (D)
(D)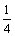
(9)某赛季足球比赛的计分规则是:胜一场,得3分;平一场,得1分;负一场,得0分,一球队打完15场,积33分,若不考虑顺序,该队胜、负、平的情况共有
(A)3种 (B)4种 (C)5种 (D)6种
(10)设坐标原点为O,抛物线y2=2x与过焦点的直线交于A、B两点,则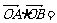
(A)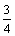 (B)
(B)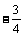 (C)3 (D)-3
(C)3 (D)-3
(11)一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜。记三种盖法屋顶面积分别为P1、P2、P3。若屋顶斜面与水平面所成的角都是α,则
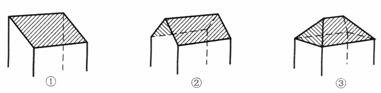
(A)P3=P2>P1 (B)P3>P2=P1
(C)P3>P2>P1 (D)P3=P2=P1
(12)如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联。连线标注的数字表示该段网线单位时间内可以通过的最大信息量。现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递。则单位时间内传递的最大信息量为
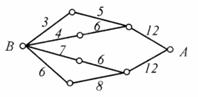
(A)20 (B)24 (C)26 (D)19
第II卷
(17)(本题满分12分)
已知a、b、c是△ABC中∠A、∠B、∠C的对边,S是△ABC的面积。若a=4,b=5,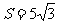 ,求c的长度.
,求c的长度.
(18)(本题满分12分)
设F1、F2为椭圆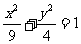 的两个焦点,P为椭圆上的一点,已知P、F1、F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,求
的两个焦点,P为椭圆上的一点,已知P、F1、F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,求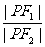 的值.
的值.
(19)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
在棱长为a的正方体OABC-O’A’B’C’中,E、F分别是棱AB、BC上的动点,且AE=BF.
(1)求证:A’F⊥C’E;
(2)当三棱锥B’-BEF的体积取得最大值时,求二面角B’-EF-B的大小。(结果用反三角函数表示)
(20)(本题满分14分)本题共有2个小题,第1小题满分10分,第2小题满分4分.
对任意一人非零复数z,定义集合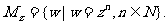
(1)设z是方程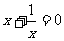 的一个根.试用列举法表示集合Mz,若在Mz中任取两个数,求其和为零的概率P;
的一个根.试用列举法表示集合Mz,若在Mz中任取两个数,求其和为零的概率P;
(2)若集合Mz中只有3个元素,试写出满足条件的一个z值,并说明理由.
(21)(本题满分16分)本题共有3个小题,第1小题满分2分,第2小题满分6分,第3小题满分8分.
用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用1个单位量的水可洗掉蔬菜上残留农药量的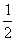 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上。设用x单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数f(x).
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上。设用x单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数f(x).
(1)试规定f(0)的值,并解释其实际意义;
(2)试根据假定写出函数f(x)应该满足的条件和具有的性质;
(3)设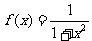 。现有a(a>0)单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较省?说明理由。
。现有a(a>0)单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较省?说明理由。
(22)(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
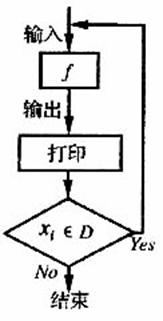
对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下:
①输入数据x0∈D,经按列发生器,其工作原理如下:
②若x1∈D,则数列发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2= f(x1),并依此规律继续下去,现定义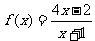 .
.
(1)若输入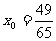 ,则由数列发生器产生数列{xn}。请写出数列{xn}的所有项:
,则由数列发生器产生数列{xn}。请写出数列{xn}的所有项:
(2)若要数列发生器产生一个无穷的常数数列,试求输入的初始数据x0的值;
(3)若输入x0时,产生的无穷数列{xn}满足;对任意正整数n,均有xn > xn+1,求x0的取值范围。
(13)a=3是直线ax+2y+3a=0和直线3x+(a-1)y=a-7平行且不重合的
(A)充分非必要条件 (B)必要非充分条件
(C)充要条件 (D)既非充分也非必要条件
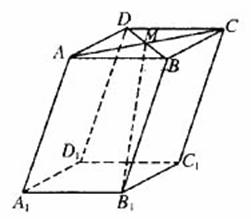
(14)如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点.若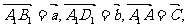 则下列向量中与
则下列向量中与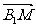 相等的向量是
相等的向量是
(A)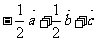 (B)
(B)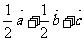
(C)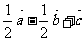 (D)
(D)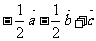
(15)已知a、b为两条不同的直线,α、β为两上不同的平面,且a⊥α、b⊥β,则下列命题中的假命题是
(A)若a∥b,则a∥β. (B)若α⊥β,则a⊥b.
(C)若a、b相交,则α、β相交. (D)若α、β相交,则a、b相交.
(16)用计算器验算函数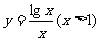 的若干个值,可以猜想下列命题中的真命题只能是
的若干个值,可以猜想下列命题中的真命题只能是
(A)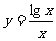 在(1,+∞)上是单调减函数
在(1,+∞)上是单调减函数
(B)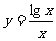 ,x∈(1,+∞)有最小值
,x∈(1,+∞)有最小值
(C)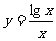 ,x∈(1,+∞)的值域为
,x∈(1,+∞)的值域为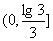
(D)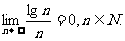
(1) 设函数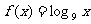 ,则满足
,则满足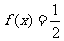 的x值为
.
的x值为
.
(2)设数列{a n}的首项a1=-7,则满足 则a1+a2+…+a17= .
则a1+a2+…+a17= .
(3)设P为双曲线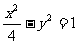 上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是
.
上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是
.
(4)设集合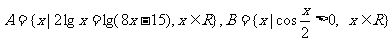 ,则A∩B的元素个数为
个.
,则A∩B的元素个数为
个.
(5)抛物线x2-4y-3=0的焦点坐标为 .
(6)设数列{a n}是公比q>0的等比数列,Sn是它的前n项和,若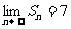 ,则此数列的首项a1的取值范围是
.
,则此数列的首项a1的取值范围是
.
(7)某餐厅供应客饭,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种。现在餐厅准备了5种不同的荤菜,若要保证每位顾客有200种以上的不同选择,则餐厅至少还需准备不同的素菜品种 种.(结果用数值表示)
(8)在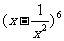 的二项展开式中,常数项为
.
的二项展开式中,常数项为
.
(9)设x=sin α,且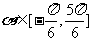 ,则arccosx的取值范围是
.
,则arccosx的取值范围是
.
(10)利用下列盈利表中的数据进行决策,应选择的方案是 .
|
自然状况 |
方案 盈利(万元) 概率 |
A1 |
A2 |
A3 |
A4 |
|
S1 |
0.25 |
50 |
70 |
-20 |
98 |
|
S2 |
0.30 |
65 |
26 |
52 |
82 |
|
S3 |
0.45 |
26 |
16 |
78 |
-10 |
(11)已知两个圆: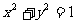 ①与
①与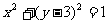 ②,则由①式减去②式可得上述两圆的对称轴方程。将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例。推广的命题为:
②,则由①式减去②式可得上述两圆的对称轴方程。将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例。推广的命题为:
.
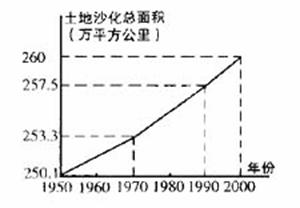
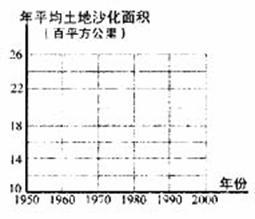
(12)据报道,我国目前已成为世界上受荒漠化危害最严重的国家之一,左下图表示我国土地沙化总面积在上个世纪五六十年代、七八十年代、九十年代的变化情况,由图中的相关信息,可将上述有关年代中,我国年平均土地沙化面积在右下图中图示为:
(17)(本小题满分12分)
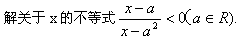
(18)(本小题满分12分)
如图,用A、B、C三类不同的元件连接成两个系统N1、N2.当元件A、B、C都正常工作时,系统N1正常工作;当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作.已知元件A、B、C正常工作的概率依次为0.80,0.90,0.90.分别求系统N1、N2正常工作的概率P1、P2.
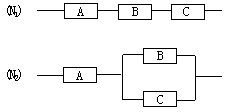
(19)(本小题满分12分)
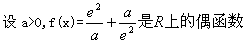
(Ⅰ)求a的值:
(Ⅱ)证明f(X)在(0,+∞)上是增函数
注意:考生在(20甲)、(20乙)两题中选一题作答,如果两题都答,只以(20甲)计分.
(20甲)(本小题满分12分)
如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox//BC,Oy//AB.E为VC中点,正四棱锥底面边长为2a,高为h.
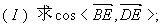
(Ⅱ)记面BCV为а,面DCV为β,若∠BED是二面角а-VC-β的平面角,求cos∠BED的值
(20乙)(本小题满分12分)
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=900,SA⊥面ABCD,SA=AB=BC=1,AD=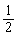 .
.
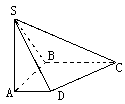
(Ⅰ)求四棱锥S-ABCD的体积;
(Ⅱ)求面SCD与面SBA所成的二面角的正切值.
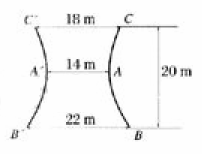
(21)某电厂冷却塔的外形是如图所示双曲线的一部分绕其中轴(即双曲线的虚轴)旋转所成的曲面,其中A、A是又曲线的顶点,C、C是冷却塔上口直径的两个端点,B、B是下底直径的两个端点,已知AAˊ=14m,CCˊ=18=22m,塔高20m。
(Ⅰ)建立坐标系并写出该双曲线方程:
(Ⅱ)求冷却塔的容积(精确到10m3,塔壁厚度不计,π取3.14).
(22)(本小题满分14分)
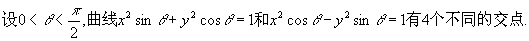
(Ⅰ)求θ的取值范围;
(Ⅱ)证明这4个交点共圆,并求圆半径的取值范围.
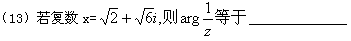
(14)一个袋子里装有大小相同的3个红球和2个黄球,从中同时取出2个,则其中含红球个数的数学期望是_______________. (用数字作答)
(15)在空间中,
①若四点不共面,则这四点中任何三点都不共线.
②若两条直线没有公共点,则这两条线是异面直线.
以上两个命题中,逆命题为真命题的是__________(把符合要求的命题序号都填上).
(16)设{an}是公比为q的等比数列,Sn是它的前n项和.若{Sn}是等差数列,则q=_______.
(1)函数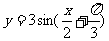 的周期,振幅依次是
的周期,振幅依次是
(A)4π、3 (B)4π、-3 (C)π、3 (D)π、-3
(2)若Sn是数列{an}的前n项和,且Sn=n2,则{an}是
(A)等比数列,但不是等差数列 (B)等差数列,但不是等比数列
(C)等差数列,而且也是等比数列 (D)既非等比数列又非等差数列
(3)过点A(1,-1)、B(-1,1)且圆心在直线x+y-2=0上的圆的方程是
(A)(x-3)2+(y+1)2=4 (B)(x+3)2+(y-1)2=4
(C)(x-1)2+(y-1)2=4 (D)(x+1)2+(y+1)2=4
(4)若定义在区间(-1,0)内的函数f(x)=log2a(x+1)满足f(x)>0,则a的取值范围是
(A)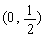 (B)
(B)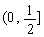 (C)
(C)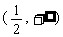 (D)
(D)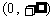
(5)若定义在区间(-1,0)内的函数f(x)=log2a(x+1)满足f(x)>0,则a的取值范围是
(A)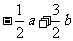 (B)
(B)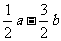 (C)
(C)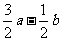 (D)
(D)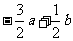
(6)设A、B是x轴上的两点,点P的横坐标为2且|PA|=|PB|.若直线PA的方程为x-y+1=0,则直线PB的方程是
(A)x+y-5=0 (B)2x-y-1=0 (C)2y-x-4=0 (D)2x+y-7=0
(7)若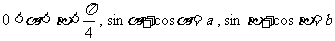 ,则
,则
(A)a<b (B)a>b (C)ab<1 (D)ab>2
(8)函数y=1+3x-x2有
(A)极小值-1,极大值1 (B)极小值-2,极小值3
(C)极小值-2,极大值2 (D)极小值-1,极大值3
(9)某赛季足球比赛的计分规则是:胜一场,得3分;平一场,得1分;负一场,得0 分. 一球队打完15场,积33分.若不考虑顺序,该队胜、负、平的可能情况共有
(A)3种 (B)4种 (C)5种 (D)6种
(10)设坐标原点为O,抛物线y2=2x与过焦点的直线交于A、B两点,则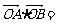
(A)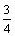 (B)
(B)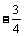 (C)3 (D)-3
(C)3 (D)-3
(11)一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜.记三种盖法屋顶面积分别为P1、P2、P3. 若屋顶斜面与水平面所成的角都是а, 则

(A)P3>P2>P1 (B)P3>P2=P1 (C)P3=P2>P1 (D)P3=P2=P1
(12)如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为
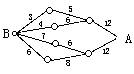
(A)26 (B)24 (C)20 (D)19
第Ⅱ卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com