
(13)从含有500个个体的总体中一次性地抽取25个个体,假定其中每个个体被抽到的概率相等,那么总体中的每个个体被抽取的概率等于________。
(14)椭圆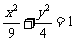 的焦点为
的焦点为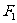 、
、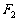 ,点P为其上的动点,当
,点P为其上的动点,当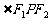 为钝角时,点P横坐标的取值范围是________。
为钝角时,点P横坐标的取值范围是________。
(15)设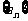 是首项为1的正项数列,且
是首项为1的正项数列,且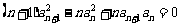 (
(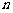 =1,2,
3,…),则它的通项公式是
=1,2,
3,…),则它的通项公式是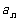 =________。
=________。
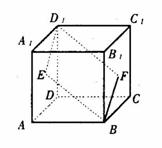
(16)如图,E、F分别为正方体的面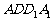 、面
、面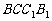 的中心,则四边形
的中心,则四边形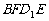 在该正方体的面上的射影可能是_______。(要求:把可能的图的 序号都填上)
在该正方体的面上的射影可能是_______。(要求:把可能的图的 序号都填上)
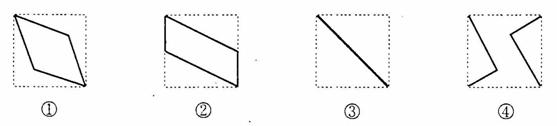
四个选项中,只有一项是符合题目要求的。
(1)设集合A=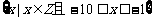 ,B=
,B=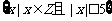 ,则A∪B中的元素个数是
,则A∪B中的元素个数是
(A)11 (B)10 (C)16 (D)15
(2)设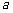 、
、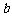 、
、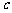 是任意的非零平面向量,且相互不共线,则
是任意的非零平面向量,且相互不共线,则
①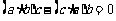 ;
②
;
②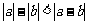
③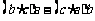 不与
不与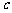 垂直
④
垂直
④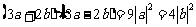
中,是真命题的有
(A)①② (B)②③ (C)③④ (D)②④
(3)一个长方体共一项点的三个面的面积分别是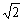 ,
,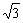 ,
,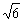 ,这个长方体
对角线的长是
,这个长方体
对角线的长是
(A)2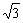 (B)3
(B)3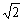 (C)
(C)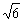 (D)6
(D)6
(4)已知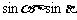 ,那么下列命题成立的是
,那么下列命题成立的是
(A)若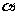 、
、 是第一象限角,则
是第一象限角,则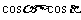
(B)若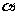 、
、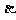 是第二象限角,则
是第二象限角,则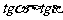
(C)若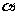 、
、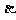 是第三象限角,则
是第三象限角,则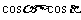
(D)若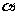 、
、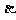 是第四象限角,则
是第四象限角,则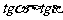
(5)函数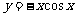 的部分图象是
的部分图象是

(6)《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过 800元的部分不必纳税,超过800元的部分为全月应纳税所得额。此项税款按下表分段累进计算:
|
全月应纳税所得额 |
税率 |
|
不超过500元的部分 |
5% |
|
超过500元至2000元的部分 |
10% |
|
超过2000元至5000元的部分 |
15% |
|
… |
… |
某人一月份应交纳此项税款26.78元,则他的当月工资、薪金所得介于
(A)800~900元 (B)900~1200元
(C)1200~1500元 (D)1500~2800元
(7)若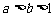 ,P=
,P=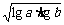 ,Q=
,Q=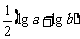 ,R=
,R=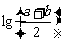 ,则
,则
(A)R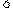 P
P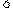 Q
(B)P
Q
(B)P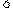 Q
Q 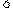 R
R
(C)Q 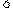 P
P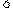 R
(D)P
R
(D)P 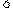 R
R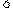 Q
Q
(8)已知两条直线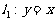 ,
,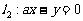 ,其中
,其中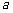 为实数。当这两条直线的夹角在
为实数。当这两条直线的夹角在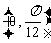 内变动时,
内变动时,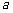 的取值范围是
的取值范围是
(A)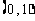 (B)
(B)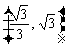 (C)
(C)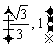 ∪
∪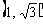 (D)
(D)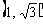
(9)一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是
(A)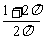 (B)
(B)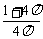 (C)
(C)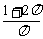 (D)
(D)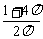
(10)过原点的直线与圆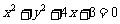 相切,若切点在第三象限,则该直线的方程是
相切,若切点在第三象限,则该直线的方程是
(A)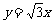 (B)
(B)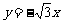 (C)
(C)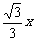 (D)
(D)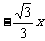
(11)过抛物线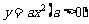 的焦点F作一条直线交抛物线于P、Q两点,若线段PF与FQ的长分别是
的焦点F作一条直线交抛物线于P、Q两点,若线段PF与FQ的长分别是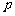 、
、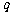 ,则
,则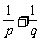 等于
等于
(A)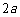 (B)
(B)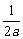 (C)
(C)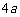 (D)
(D)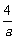
(12)二项式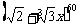 的展开式中系数为有理数的项共有
的展开式中系数为有理数的项共有
(A)6项 (B)7项 (C)8项 (D)9项
第Ⅱ卷
(17)(本题满分12分)
已知椭圆C的焦点分别为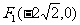 和
和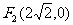 ,长轴长为6,设直线
,长轴长为6,设直线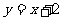 交椭圆C于A、B两点,求线段AB的中点坐标。
交椭圆C于A、B两点,求线段AB的中点坐标。
(18)(本题满分12分)
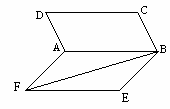
如图所示四面体ABCD中,AB、BC、BD两两互相垂直,且AB=BC=2,E是AC中点,异面直线AD与BE所成的角的大小为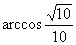 ,求四面体ABCD的体积。
,求四面体ABCD的体积。

(19)(本题满分14分)本题共有2个小题,第1个小题满分6分,第2小题满分8分。
已知函数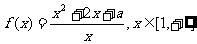 。
。
(Ⅰ)当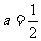 时,求函数
时,求函数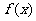 的最小值。
的最小值。
(Ⅱ)若对任意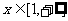 ,
,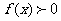 恒成立,试求实数
恒成立,试求实数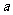 的取值范围。
的取值范围。
(20)(本题满分14分)本题共有2个小题,第1小题满分4分,第2小题满分10分。
根据指令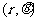
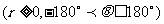 ,机器人在平面上能完成下列动作:先原地旋转角度
,机器人在平面上能完成下列动作:先原地旋转角度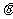 (
(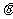 为正时,按逆时针方向旋转
为正时,按逆时针方向旋转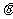 ,
,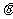 为负时,按顺时针方向旋转-
为负时,按顺时针方向旋转-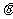 ),再朝其面对的方向沿直线行走距离
),再朝其面对的方向沿直线行走距离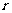 。
。
(Ⅰ)现机器人在直角坐标系的坐标原点,且面对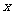 轴正方向,试给机器人下一个指令,使其移动到点(4,4)。
轴正方向,试给机器人下一个指令,使其移动到点(4,4)。
(Ⅱ)机器人在完成该指令后,发现在点(17,0)处有一小球正向坐标原点作匀速直线滚动,已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令(结果精确到小数点后两位)。
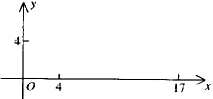
(21)(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分。
在XOY平面上有一点列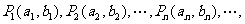 对每个自然数
对每个自然数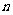 ,点
,点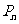 位于函数
位于函数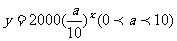 的图象上,且点
的图象上,且点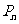 ,点
,点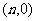 与点
与点 构成一个以
构成一个以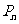 为顶点的等腰三角形
为顶点的等腰三角形
(Ⅰ)求点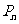 的纵坐标
的纵坐标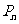 的表达式;
的表达式;
(Ⅱ)若对每个自然数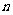 ,以
,以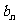 ,
,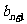 ,
,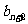 为边长能构成一个三角形,求
为边长能构成一个三角形,求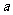 的取值范围;
的取值范围;
(Ⅲ)设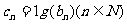 ,若
,若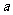 取(2)中确定的范围内的最小整数,问数列
取(2)中确定的范围内的最小整数,问数列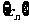 前多少项的和最大?试说明理由。
前多少项的和最大?试说明理由。
(22)(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分。
已知复数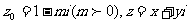 和,其中
和,其中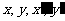 均为实数,
均为实数,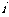 为虚数单位,且对于任意复数
为虚数单位,且对于任意复数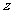 ,有
,有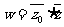 ,
,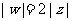 。
。
(Ⅰ)试求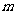 的值,并分别写出
的值,并分别写出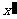 和
和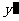 用
用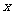 、
、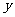 表示的关系式:
表示的关系式:
(Ⅱ)将(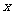 、
、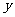 )用为点
)用为点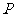 的坐标,(
的坐标,(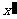 、
、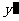 )作为点
)作为点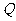 的坐标,上述关系式可以看作是坐标平面上点的一个变换:它将平面上的点
的坐标,上述关系式可以看作是坐标平面上点的一个变换:它将平面上的点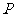 变到这一平面上的点
变到这一平面上的点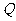 。已知点
。已知点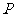 经该变换后得到的点
经该变换后得到的点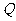 的坐标为
的坐标为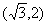 ,试求点
,试求点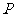 的坐标;
的坐标;
(Ⅲ)若直线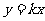 上的任一点经上述变换后得到的点仍在该直线上,试求
上的任一点经上述变换后得到的点仍在该直线上,试求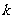 的值。
的值。
(13)函数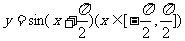 是
是
(A)增函数 (B)减函数 (C)偶函数 (D)奇函数
(14)设有不同的直线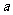 、
、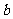 和不同的平面
和不同的平面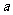 、
、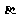 、
、 ,给出下列三个命题:
,给出下列三个命题:
(1)若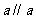 ,
,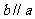 ,则
,则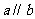 。
。
(2)若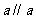 ,
,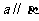 ,则
,则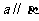 。
。
(3)若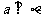 ,
,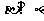 ,则
,则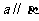 。
。
其中正确的个数是
(A)0 (B)1 (C)2 (D)3
(15)若集合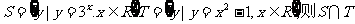 是
是
(A)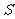 (B)
(B)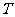 (C)
(C)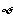 (D)有限集
(D)有限集
(16)下列命题中正确的命题是
(A)若点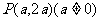 为角
为角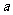 终边上一点,则
终边上一点,则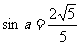 。
。
(B)同时满足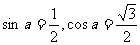 的角
的角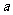 有且只有一个。
有且只有一个。
(C)当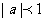 时,
时,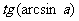 的值恒正。
的值恒正。
(D)三角方程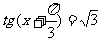 的解集为
的解集为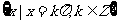 。
。
(1)已知向量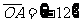 、
、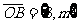 ,若
,若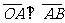 ,则
,则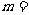 。
。
(2)函数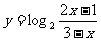 的定义域为
。
的定义域为
。
(3)圆锥曲线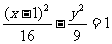 的焦点坐标是
。
的焦点坐标是
。
(4)计算: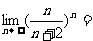 。
。
(5)已知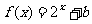 的反函数为
的反函数为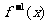 ,若
,若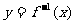 的图像经过点
的图像经过点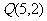 ,则
,则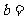 。
。
(6)根据上海市人大十一届三次会议上的市政府工作报告,1999年上海市完成GDP(GDP是指国内生产总值)4035亿元,2000年上海市GDP预期增长9%,市委、市府提出本市常住人口每年的自然增长率将控制在0.08%,若GDP与人口均按这样的速度增长,则要使本市年人均GDP达到或超过1999年的2倍,至少需 年。(按:1999年本市常住人口总数约1300万)
(7)命题A:底面为正三角形,且顶点在底面的射影为底面中心的三棱锥是正三棱锥,命题A的等价命题B可以是:底面为正三角形,且 的三棱锥是正三棱锥。
(8)设函数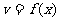 是最小正周期为2的偶函数,它在区间[0,1]上的图像为 如图所示的线段AB,则在区间[1,2]上,
是最小正周期为2的偶函数,它在区间[0,1]上的图像为 如图所示的线段AB,则在区间[1,2]上,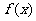 =
。
=
。
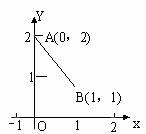
(9)在二项式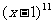 的展开式中,系数是小的项的系数为
。(结果用数值表示)
的展开式中,系数是小的项的系数为
。(结果用数值表示)
(10)有红、黄、蓝三种颜色的旗帜各3面,在每种颜色的3面旗帜上分别标上号码1、2和3,现任取出3面,它们的颜色与号码不相同的概率是 。
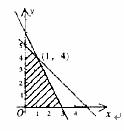
(11)图中阴影部分的点满足不等式组 ,在这些点中,使目标函数
,在这些点中,使目标函数 取得最大值的点的坐标是
。
取得最大值的点的坐标是
。
(12)在等差数列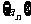 中,若
中,若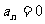 ,则有等式
,则有等式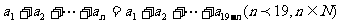 成立,类比上述性质,相应地:在等比数列
成立,类比上述性质,相应地:在等比数列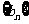 中,若
中,若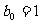 ,则有等式
成立。
,则有等式
成立。
第Ⅱ卷
(17)(本题满分12分)
已知椭圆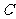 的焦点分别为
的焦点分别为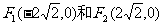 ,长轴长为6,设直
,长轴长为6,设直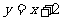 交椭圆
交椭圆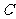 于
于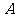 、
、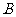 两点,求线段
两点,求线段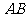 的中点坐标。
的中点坐标。
(18)(本题满分12分)
如图所示四面体ABCD中,AB、BC、BD两两互相垂直,且AB=BC=2,E是AC中点,异面直线AD与BE所成的角的大小为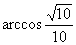 ,求四面体ABCD的体积。
,求四面体ABCD的体积。

(19)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分。已知函数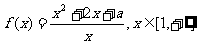 。
。
(Ⅰ)当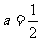 时,求函数
时,求函数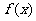 的最小值:
的最小值:
(Ⅱ)若对任意 恒成立,试求实数
恒成立,试求实数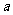 的取值范围。
的取值范围。
(20)(本题满分14分)本题共有2个小题,第1小题满分4分,第2小题满分10分。
根据指令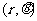
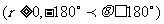 ,机器人在平面上能完成下列动作:先原地旋转角度
,机器人在平面上能完成下列动作:先原地旋转角度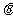 (
(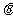 为正时,按逆时针方向旋转
为正时,按逆时针方向旋转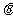 ,
,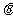 为负时,按顺时针方向旋转-
为负时,按顺时针方向旋转-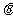 ),再朝其面对的方向沿直线行走距离
),再朝其面对的方向沿直线行走距离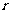 。
。
(Ⅰ)现机器人在直角坐标系的坐标原点,且面对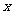 轴正方向,试给机器人下一个指令,使其移动到点(4,4)。
轴正方向,试给机器人下一个指令,使其移动到点(4,4)。
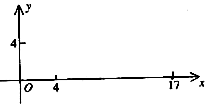
(Ⅱ)机器人在完成该指令后,发现在点(17,0)处有一小球正向坐标原点作匀速直线滚动,已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令(结果精确到小数点后两位)。
(21)(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3 小题满分6分。
在XOY平面上有一点列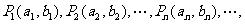 对每个自然数
对每个自然数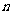 ,点
,点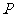 ,位于函数
,位于函数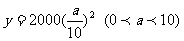 的图象上,且点
的图象上,且点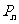 ,点
,点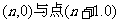 构成一个以
构成一个以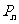 为顶点的等腰三角形。
为顶点的等腰三角形。
(Ⅰ)求点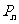 的纵坐标
的纵坐标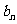 的表达式。
的表达式。
(Ⅱ)若对每个自然数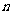 ,以
,以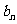 ,
,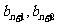 为边长能构成一个三角形,求
为边长能构成一个三角形,求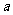 取值范围。
取值范围。
(Ⅲ)设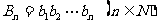 ,若
,若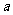 取(2)中确定的范围内的最小整数,求数列
取(2)中确定的范围内的最小整数,求数列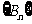 的最大项的项数。
的最大项的项数。
(22)(本小题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分。
已知复数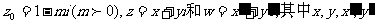 均为实数,
均为实数,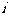 为虚数单位,且对于任意复数
为虚数单位,且对于任意复数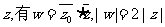 。
。
(Ⅰ)试求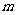 的值,并分别写出
的值,并分别写出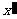 和
和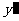 用
用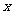 、
、 表示的关系式;
表示的关系式;
(Ⅱ)将(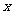 、
、 )作为点
)作为点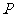 的坐标,(
的坐标,(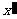 、
、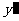 )作为点
)作为点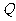 的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点
的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点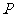 变到这一平面上的点
变到这一平面上的点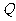 ,当点
,当点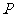 在直线
在直线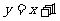 上移动时,试求点
上移动时,试求点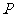 经该变换后得到的点
经该变换后得到的点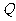 的轨迹方程;
的轨迹方程;
(Ⅲ)是否存在这样的直线:它上面的任一点经上述变换后得到的点仍在该直线上?若存在,试求出所有这些直线;若不存在,则说明理由。
(13)复数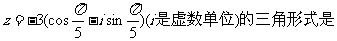
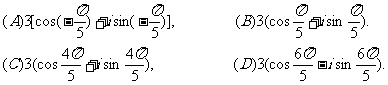
(14)设有不同的直线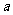 、
、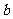 和不同的平面
和不同的平面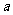 、
、 、
、 ,给出下列三个命题:
,给出下列三个命题:
(1)若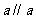 ,
,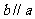 ,则
,则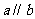 。
(2)若
。
(2)若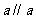 ,
,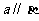 ,则
,则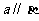 。
。
(3)若 ,
,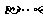 ,则
,则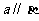 。
。
其中正确的个数是
(A)0. (B)1. (C)2. (D)3.
(15)若集合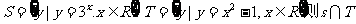 是:
是:
 .
.
(16)下列命题中正确的命题是
(A)若点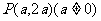 为角
为角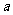 终边上一点,则
终边上一点,则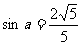 。
。
(B)同时满足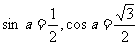 的角
的角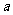 有且只有一个。
有且只有一个。
(C)当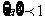 时,
时,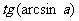 的值恒正。
的值恒正。
(D)三角方程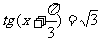 的解集为
的解集为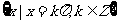 。
。
第Ⅱ卷
(1)已知向量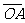 (-1,2)、
(-1,2)、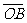 =(3,m),若
=(3,m),若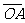 ┴
┴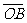 ,则m=
。
,则m=
。
(2)函数,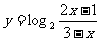 的定义域为
。
的定义域为
。
(3)圆锥曲线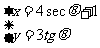 的焦点坐标是
。
的焦点坐标是
。
(4)计算: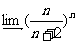 =
。
=
。
(5)已知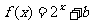 的反函数为
的反函数为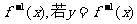 的图象经过点
的图象经过点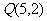 ,则
,则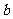 =
。
=
。
(6)根据上海市人大十一届三次会议上的市政府工作报告,1999年上海市完成GDP(GDP是指国内生产总值)4035亿元,2000年上海市GDP预期增长9%,市委、市府提出本市常住人口每年的自然增长率将控制在0.08%,若GDP与人口均按这样的速度增长,则要使本市年人均GDP达到或超过1999年的2倍,至少需 年。
(按:1999年本市常住人口总数约1300)
(7)命题A:底面为正三角形,且顶点在底面的射影为底面中心的三棱锥是正三棱锥, 命题A的等价题B可以是:底面为正三角形,且 的三棱锥是正三棱锥
(8)设函数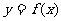 是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图所示的线段
是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图所示的线段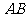 ,则在区间[1,2]上
,则在区间[1,2]上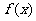 =
。
=
。
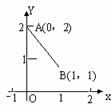
(9)在二项式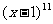 的展开式中,系数最小的项的系数为
,(结果用数值表示)
的展开式中,系数最小的项的系数为
,(结果用数值表示)
(10)有红、黄、蓝三种颜色的旗帜各3面,在每种颜色的3面旗帜上分别标上号码1、2和3,现任取出3面,它们的颜色与号码均不相同的概率是 。
(11)在极坐标系中,若过点(3,0)且与极轴垂直的直线交曲线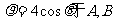 两点,则
两点,则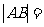 。
。
(12)在等差数列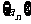 中,若
中,若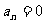 ,则有等式
,则有等式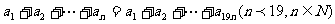 成立,类比上述性质,相就夺:在等此数列
成立,类比上述性质,相就夺:在等此数列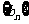 中,若
中,若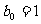 ,则有等式 成立。
,则有等式 成立。
(20)(本小题满分11分)
解不等式loga(x+1-a)>1.
(21)(本小题满分12分)
设等比数列{an}的前n项和为Sn.若S3+S6=2S9,求数列的公比q.
(22)(本小题满分12分)
(23)(本小题满分12分)
[注意:本题的要求是,参照标号①的写法,在标号②、③、④、⑤的横线上填写适当步骤,完成(Ⅰ)证明的全过程;并解答(Ⅱ).]
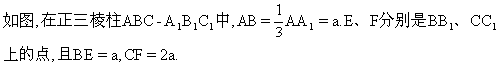
(Ⅰ)求证:面AEF⊥面ACF;
(Ⅱ)求三棱锥A1-AEF的体积.
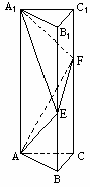
(Ⅰ)证明:
① ∵BE=a,CF=2a,BE∥CF,延长FE与CB延长线交于D,连结AD.
∴△DBE∽△DCF
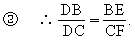
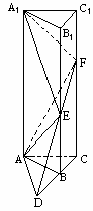
③ ∴DB=AB.
④ ∴DA⊥AC.
⑤ ∴FA⊥AD.
∴面AEF⊥面ACF.
(24)(本小题满分10分)
某地现有耕地10000公顷.规划10年后粮食单产比现在增加22%,人均粮食占有量比现在提高10%.如果人口年增长率为1%,那么耕地平均每年至多只能减少多少公顷(精确到1公顷)?
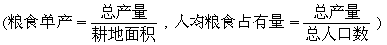
(25)(本小题满分12分)
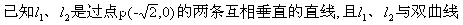
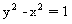
各有两个交点,分别为A1、B1和A2、B2.
(Ⅰ)求l1的斜率k1的取值范围;
(Ⅱ)若A1恰是双曲线的一个顶点,求│A2B2│的值.
(16)已知点(-2,3)与抛物线y2=2px(p>0)的焦点的距离是5,则p=
(17)正六边形的中心和顶点共7个点,以其中3个点为顶点的三角形共有 个.(用数字作答)
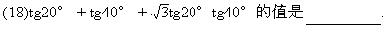
(19)如图,正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角的余弦值是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com