
4.函数f(x)=Msin(ωx+ρ)(ω>0)在区间[a,b]上是增函数,且f(a)=-M,f(b)=M,则函数g(x)=Mcos(ωx+ρ)在[a,b]上
A.是增函数 B.是减函数
C.可以取得最大值M D.可以取得最小值-M
3.若函数y=f(x)的反函数是y=g(x),f(a)=b,ab≠0,则g(b)等于
A.a B.a-1 C.b D.b-1
2.已知映射f:A→B,其中,集合A={-3,-2,-1,1,2,3,4},集合B中的元素都是A中元素在映射f下的象,且对任意的a∈A,在B中和它对应的元素是|a|,则集合B中元素的个数是
A.4 B.5 C.6 D.7
1.如图,I是全集,M、P、S是I的3个子集,则阴影部分所表示的集合是
A.(M∩P)∩S B.(M∩P)∪S
C.(M∩P)∩ 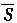 D.(M∩P)∪
D.(M∩P)∪ 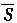
(17)(本小题满分12分)
设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx,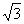 sin2x),x∈R.
sin2x),x∈R.
(Ⅰ)若f(x)=1-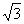 且x∈[-
且x∈[-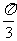 ,
,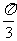 ],求x;
],求x;
(Ⅱ)若函数y=2sin2x的图象按向量c=(m,n)(|m|<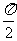 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
(18)(本小题满分12分)
甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.
(Ⅰ)分别求甲、乙两人考试合格的概率;
(Ⅱ)求甲、乙两人至少有一人考试合格的概率.
(19)(本小题满分12分)
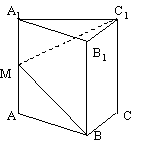
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2 ,M为AB的中点.
,M为AB的中点.
(Ⅰ)证明:AC⊥SB;
(Ⅱ)求二面角N-CM-B的大小;
(Ⅲ)求点B到平面SCM的距离.
(20)(本小题满分12分)
某企业2003年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+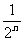 )万元(n为正整数).
)万元(n为正整数).
(Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为An万元,进行技术改造后的累计纯利润为Bn万元(须扣除技术改造资金),求An、Bn的表达式;
(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
(21)(本小题满分12分)
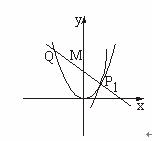
如图,P是抛物线C:y=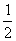 x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q.
x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q.
(Ⅰ)当点P的横坐标为2时,求直线l的方程;
(Ⅱ)当点P在抛物线C上移动时,求线段PQ中点M的轨迹方程,并求点M到x轴的最短距离
(22)(本小题满分14分)
已知f(x)=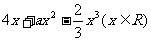 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)=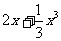 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
(13)直线x+2y=0被曲线x2+y2-6x-2y-15=0所截得的弦长等于 .
(14)设函数 则实数a的取值范围是
.
则实数a的取值范围是
.
(15)一个总体中有100个个体,随机编号0,1,2,…,99,依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=6,则在第7组中抽取的号码是 .
(16)将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器,.当这个正六棱柱容器的底面边长为 时,其容积最大.
(1)设集合U={1,2,3,4,5},A={1,3,5},B={2,3,5},则 (A∩B)等于
(A){1,2,4} (B){4} (C){3,5} (D)ø
(2) 的值是
的值是
(A)2 (B)2+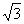 (C)4 (D)
(C)4 (D)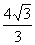
(3)命题p:若a、b∈R,则|a|+|b|>1是|a+b|>1的充要条件;
命题q:函数y=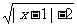 的定义域是(-∞,-1
的定义域是(-∞,-1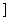 ∪[3,+∞
∪[3,+∞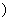 .则
.则
(A)“p或q”为假 (B)“p且q”为真
(C)p真q假 (D)p假q真
(4)已知F1、F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A、B两点,若△ABF2是正三角形,则这个椭圆的离心率是
(A)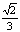 (B)
(B)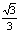 (C)
(C)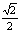 (D)
(D)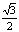
(5)设Sn是等差数列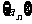 的前n项和,若
的前n项和,若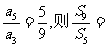
(A)1 (B)-1 (C)2 (D)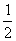
(6)已知m、n是不重合的直线,α、β是不重合的平面,有下列命题:
①若m α,n∥α,则m∥n;
α,n∥α,则m∥n;
②若m∥α,m∥β,则α∥β;
③若α∩β=n,m∥n,则m∥α且m∥β;
④若m⊥α,m⊥β,则α∥β.
其中真命题的个数是
(A)0 (B)1 (C)2 (D)3
(7)已知函数y=log2x的反函数是y=f-1(x),则函数y= f-1(1-x)的图像是 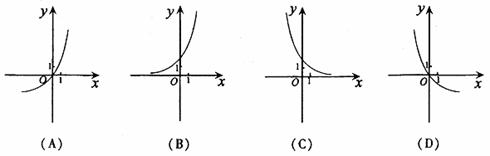
(8)已知a、b是非零向量且满足(a-2b) ⊥a,(b-2a) ⊥b,则a与b的夹角是
(A)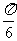 (B)
(B)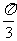 (C)
(C)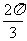 (D)
(D)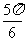
(9)已知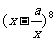 展开式中常数项为1120,其中实数a是常数,则展开式中各项系数的和是
展开式中常数项为1120,其中实数a是常数,则展开式中各项系数的和是
(A)28 (B)38 (C)1或38 (D)1或28
(10)如图,A、B、C是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60º,O为球心,则直线OA与截面ABC所成的角是
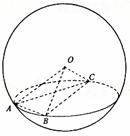
(A)arcsin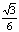 (B)arccos
(B)arccos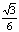 (C)arcsin
(C)arcsin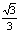 (D)arccos
(D)arccos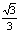
(11)定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈[3,4]时,f(x)= x-2,则
(A)f(sin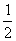 )<f(cos
)<f(cos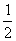 )
(B)f(sin
)
(B)f(sin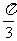 )>f(cos
)>f(cos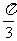 )
)
(C)f(sin1)<f(cos1)
(D)f(sin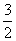 )>f(cos
)>f(cos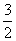 )
)
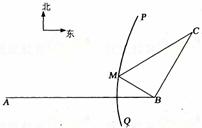
(12)如图,B地在A地的正东方向4 km处,C地在B地的北偏东30°方向2 km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2km,现要在曲线PQ上任意选一处M建一座码头,向B、C两地转运货物,经测算,从M到B、C两地修建公路的费用都是a万元/km、那么修建这两条公路的总费用最低是
(A)(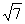 +1)a万元 (B)(2
+1)a万元 (B)(2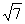 -2) a万元
-2) a万元
(C)2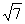 a万元 (D)(
a万元 (D)(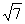 -1) a万元
-1) a万元
第Ⅱ卷
(15)(本小题满分14分)
在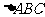 中,
中,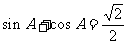 ,
,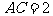 ,
,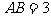 ,求
,求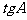 的值和
的值和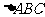 的面积
的面积
(16)(本小题满分14分)
如图,在正三棱柱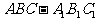 中,AB=2,
中,AB=2,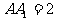 ,由顶点B沿棱柱侧面经过棱
,由顶点B沿棱柱侧面经过棱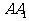 到顶点
到顶点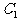 的最短路线与
的最短路线与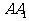 的交点记为M,求:
的交点记为M,求:
(I)三棱柱的侧面展开图的对角线长;
(II)该最短路线的长及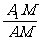 的值;
的值;
(III)平面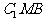 与平面ABC所成二面角(锐角)的大小
与平面ABC所成二面角(锐角)的大小
(17)(本小题满分14分)
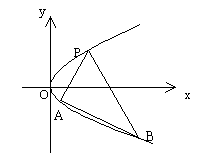
如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(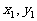 ),B(
),B(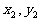 )均在抛物线上。
)均在抛物线上。
(I)写出该抛物线的方程及其准线方程;
(II)当PA与PB的斜率存在且倾斜角互补时,求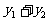 的值及直线AB的斜率
的值及直线AB的斜率
(18)(本小题满分14分)
函数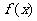 定义在[0,1]上,满足
定义在[0,1]上,满足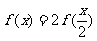 且
且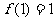 ,在每个区间
,在每个区间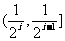 (
(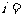 1,2……)上,
1,2……)上,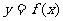 的图象都是平行于x轴的直线的一部分.
的图象都是平行于x轴的直线的一部分.
(I)求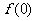 及
及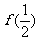 ,
,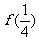 的值,并归纳出
的值,并归纳出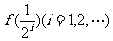 的表达式
的表达式
(II)设直线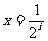 ,
,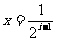 ,x轴及
,x轴及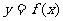 的图象围成的矩形的面积为
的图象围成的矩形的面积为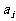 (
(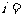 1,2…),求
1,2…),求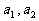 及
及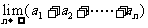 的值.
的值.
(19)(本小题满分12分)
某段城铁线路上依次有A、B、C三站,AB=5km,BC=3km,在列车运行时刻表上,规定列车8时整从A站发车,8时07分到达B站并停车1分钟,8时12分到达C站.在实际运行中,假设列车从A站正点发车,在B站停留1分钟,并在行驶时以同一速度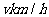 匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
(I)分别写出列车在B、C两站的运行误差;
(II)若要求列车在B,C两站的运行误差之和不超过2分钟,求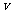 的取值范围.
的取值范围.
(20)(本小题满分12分)
给定有限个正数满足条件T:每个数都不大于50且总和L=1275.现将这些数按下列要求进行分组,每组数之和不大于150且分组的步骤是:
首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差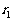 与所有可能的其他选择相比是最小的,
与所有可能的其他选择相比是最小的,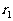 称为第一组余差;
称为第一组余差;
然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,这时的余差为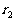 ;如此继续构成第三组(余差为
;如此继续构成第三组(余差为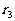 )、第四组(余差为
)、第四组(余差为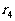 )、……,直至第N组(余差为
)、……,直至第N组(余差为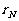 )把这些数全部分完为止.
)把这些数全部分完为止.
(I)判断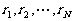 的大小关系,并指出除第N组外的每组至少含有几个数
的大小关系,并指出除第N组外的每组至少含有几个数
(II)当构成第n(n<N)组后,指出余下的每个数与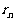 的大小关系,并证明
的大小关系,并证明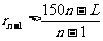 ;
;
(III)对任何满足条件T的有限个正数,证明: .
.
(9)函数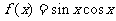 的最小正周期是______________.
的最小正周期是______________.
(10)方程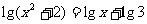 的解是______________.
的解是______________.
(11)圆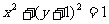 的圆心坐标是______________,如果直线
的圆心坐标是______________,如果直线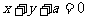 与该圆有公共点,那么实数a的取值范围是______________.
与该圆有公共点,那么实数a的取值范围是______________.
(12)某地球仪上北纬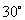 纬线的长度为
纬线的长度为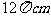 ,该地球仪的半径是__________cm,表面积是______________cm2.
,该地球仪的半径是__________cm,表面积是______________cm2.
(13)在函数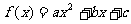 中,若a,b,c成等比数列且
中,若a,b,c成等比数列且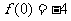 ,则
,则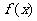 有最______________值(填“大”或“小”),且该值为______________.
有最______________值(填“大”或“小”),且该值为______________.
(14)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和. 已知数列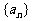 是等和数列,且
是等和数列,且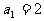 ,公和为5,那么
,公和为5,那么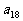 的值为______________,且这个数列的前21项和
的值为______________,且这个数列的前21项和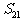 的值为______________.
的值为______________.
(1)设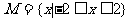 ,
,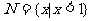 ,则
,则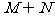 等于
等于
(A)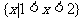 (B)
(B)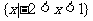
(C)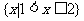 (D)
(D) 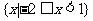
(2)满足条件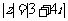 的复数
的复数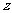 在复平面上对应点的轨迹是
在复平面上对应点的轨迹是
(A)一条直线 (B)两条直线 (C)圆 (D) 椭圆
(3)设m、n是两条不同的直线,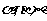 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若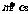 ,
,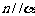 ,则
,则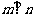 ②若
②若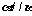 ,
, ,
,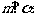 ,则
,则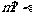
③若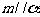 ,
,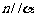 ,则
,则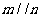 ④若
④若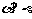 ,
,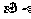 ,则
,则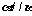
其中正确命题的序号是
(A)①和② (B)②和③ (C)③和④ (D) ①和④
(4)已知a、b、c满足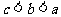 ,且
,且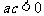 ,那么下列选项中一定成立的是
,那么下列选项中一定成立的是
(A) (B)
(B)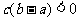 (C)
(C)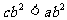 (D)
(D) 
(5)从长度分别为1,2,3,4的四条线段中,任取三条的不同取法共有n种,在这些取法中,以取出的三条线段为边可组成的三角形的个数为m,则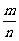 等于
等于
(A)0 (B)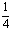 (C)
(C)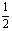 (D)
(D) 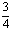
(6)如图,在正方体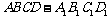 中,P是侧面
中,P是侧面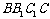 内一动点,若P到直线BC与
内一动点,若P到直线BC与
直线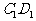 的距离相等,则动点P的轨迹所在的曲线是
的距离相等,则动点P的轨迹所在的曲线是
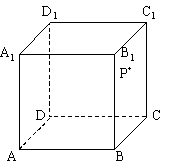
(A)直线 (B)圆 (C)双曲线 (D) 抛物线
(7)函数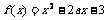 在区间[1,2]上存在反函数的充分必要条件是
在区间[1,2]上存在反函数的充分必要条件是
(A)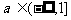 (B)
(B)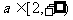
(C)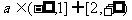 (D)
(D) 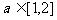
(8)函数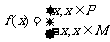 ,其中P、M为实数集R的两个非空子集,又规定
,其中P、M为实数集R的两个非空子集,又规定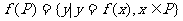 ,
,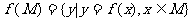 ,给出下列四个判断:
,给出下列四个判断:
①若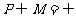 ,则
,则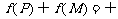 ②若
②若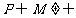 ,则
,则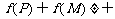
③若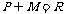 ,则
,则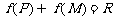 ④若
④若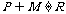 ,则
,则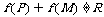
其中正确判断有
(A)3个 (B)2个 (C)1个 (D) 0个
第Ⅱ卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com