
5.数据以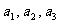 …,
…,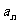 的方差为
的方差为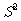 ,则数据
,则数据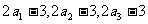 …,
…,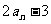 的标准差为
的标准差为
A.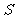 B.
B.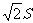 C.
C.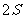 D.
D.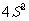
4.下图是2006年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为
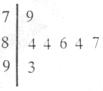
A.84,4.84 B.84,1.6 C.85,1.6 D.85,4
3.线性回归:变量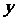 与
与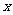 之间的回归方程
之间的回归方程
A.表示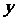 与
与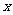 之间的函数关系
之间的函数关系
B.表示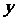 和
和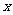 之间的不确定关系
之间的不确定关系
C.反映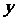 和
和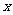 之间真实关系的形式
之间真实关系的形式
D.反映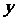 与
与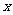 之间的真实关系达到最大限度的吻合
之间的真实关系达到最大限度的吻合
2.在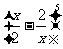 的展开式中
的展开式中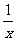 的系数等于
的系数等于
A 10 B.-10 C.20 D.-20
1.关于赋值语句的说法正确的个数是:①赋值语句中的赋值号与数学中的等号意义相同.②赋值号左边只能是变量名字,而不是表达式.③赋值号左右两边不能对换.④不能利用赋值语句进行代数式(或符号)的演算.
A.1 B.2 C.3 D.4
(17)(本小题满分12分)
已知a,b是正实数,用分析法证明: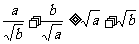
(18)(本小题满分12分)
在棱长为1的正方体船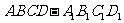 中,试在侧棱
中,试在侧棱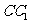 上求一点P,使得直线AP与平面
上求一点P,使得直线AP与平面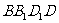 所成角为
所成角为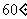 .
.
(19)(本小题满分12分)
已知函数 .
.
( I )当a=1时,曲线 和直线
和直线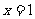 交于点P,求曲线
交于点P,求曲线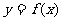 在点P处的切线方程;
在点P处的切线方程;
(Ⅱ)当a<0时,求函数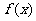 的单调递增区间.
的单调递增区间.
(20)(本小题满分12分)
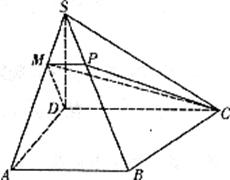
已知四棱锥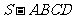 ,
,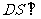 平面ABCD,四边形ABCD为直角梯形,∠DAB=∠ADC=
平面ABCD,四边形ABCD为直角梯形,∠DAB=∠ADC=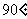 ,DS=AD=AB=l,DC=2,M是AS上一点,且AM=2MS.
,DS=AD=AB=l,DC=2,M是AS上一点,且AM=2MS.
(I)设平面DCM与棱SB相交于点P,求证:四边形DCPM是直角梯形;
(II)求平面SAD与平面SBC所成二面角的余弦值.
(21)(本小题满分12分)
已知数列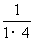 ,
,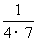 ,
,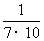 ,…,
,…,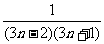 ,….
,….
(I)计算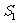 ,
, ,
,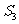 ,
,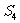 ;
;
(II)根据(I)的计算结果,猜想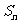 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.
(22)(本小题满分14分)
已知函数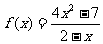 ,
, ,其定义域都在[0,1]上.
,其定义域都在[0,1]上.
(I)求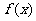 的单调区间;
的单调区间;
(Ⅱ)设a≥1,求函数g(x)的值域;
(Ⅲ)当a≥1时,若对于任意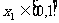 总存在
总存在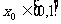 ,使得
,使得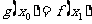 成立,求a的取值范围.
成立,求a的取值范围.
(13)(选做题:两个题选做一个,若两题都做,只以甲题记分) 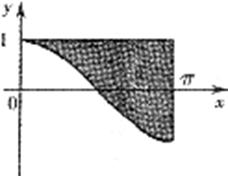
(甲)由函数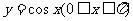 图象与直线
图象与直线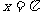 及
及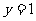 的图象围成一个封闭图形的面积是_________________.
的图象围成一个封闭图形的面积是_________________.
(乙)若复数z满足 ,那么z的共轭复数
,那么z的共轭复数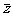 =
=
(14)已知A(1,0,0),B(0,1,0),C(0,0,1),则原点O到平面ABC的距离等于____.
(15)设 ,则
,则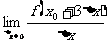 =___________.
=___________.
(16)已知,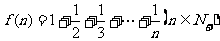 ,经计算得:
,经计算得: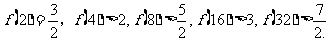 .
.
由此可推测当n≥2时,有___________________.
(1)用数学归纳法证明凸n边形对角线条数为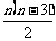 时,第一步应验证n等于
时,第一步应验证n等于
(A)1 (B)2 (C)3 (D)4
(2)数列2,5,11,20,x,47,…中的x等于
(A)27 (B)28 (C)32 (D)33
(3)设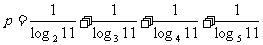 ,则
,则
(A)0<p<1 (B)1<p<2 (C)2<p<3 (D)3<p<4
(4)求由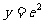 ,
, ,
,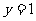 围成的曲边形的面积时,若选择x为积分变量,则积分区间为
围成的曲边形的面积时,若选择x为积分变量,则积分区间为
(A)[0,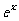 ] (B)[0,2] (C)[1,2] (D)[0,1]
] (B)[0,2] (C)[1,2] (D)[0,1]
(5)若向量a,b的坐标满足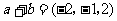 ,
,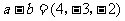 ,则a·b等于
,则a·b等于
(A)-5 (B)5 (C)7 (D)-1
(6)已知空间三点的坐标为A(1,5,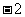 ),B(2,4,1),C(p,3,q+2),若A、B、C三点共线,则有
),B(2,4,1),C(p,3,q+2),若A、B、C三点共线,则有
(A)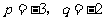 (B)
(B)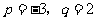
(C) (D)
(D)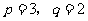
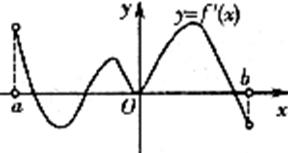
(7)函数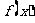 的定义域为开区间(a,b),导函数
的定义域为开区间(a,b),导函数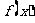 在(a,b)内的图象如图所示,则函数在开区间内有极小值点
在(a,b)内的图象如图所示,则函数在开区间内有极小值点
(A)1个 (B)2个
(C)3个 (D)4个
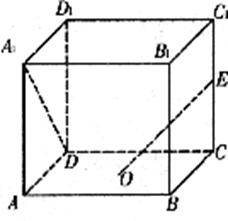
(8)如图,在棱长为2的正方体 中,O为底面的中心,E是
中,O为底面的中心,E是 ,的中点,则异面直线
,的中点,则异面直线 与EO所成角的余弦值为
与EO所成角的余弦值为
(A)0 (B)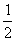
(c)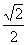 (D)
(D)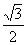
(9)已知 ,表示平面,a,b表示直线,则a∥
,表示平面,a,b表示直线,则a∥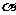 的一个充分条件是
的一个充分条件是
(A)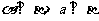 (B)
(B)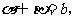 a∥b
a∥b
(C)a∥b,b∥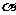 (D)a∥
(D)a∥ ,a
,a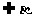
(10)给出下列命题:
①若函数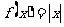 ,则
,则 ;
;
②若函数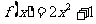 ,图象上点P(1,3)及邻近点
,图象上点P(1,3)及邻近点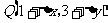 ,则
,则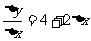 ;
;
③加速度是动点位移函数S(t)对时间t的导数;
④若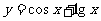 ,则
,则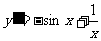
其中正确的命题有
(A)0个 (B)1个 (C)2个 (D)3个
(11)以下四图,都是同一坐标系中三次函数及其导函数的图象,其中一定不正确的序号是
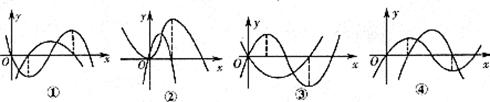
(A) ①、② (B) ①、③ (C) ③、④ (D) ①、④
(12)当x≠0时,不等式成立的是
(A)
(B)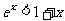
(C)当 时,
时,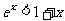 ;当
;当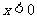 时,
时,
(D)当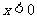 时,
时,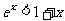 ;当
;当 时,
时,
第Ⅱ卷 (非选择题共90分)
(17)(本小题满分12分)
已知a,b是正实数,用分析法证明:
(18)(本小题满分12分)
在对人们的休闲方式的一次调查中,共调查了72人,其中女性36人男性36人.女性中有20人主要的休闲方式是看电视,另外16人主要的休闲方式是运动;男性中有8人主要的休闲方式是看电视,另外28人主要休闲方式是运动.
(I)根据以上数据建立一个2×2列联表.
(Ⅱ)判断性别与休闲方式是否有关系?请用统计学的有关知识,说明理由.
(19)(本小题满分12分)
已知函数,
(I)当a=1时,曲线 和直线
和直线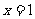 交于点P,求曲线
交于点P,求曲线 在点P处的切线方程;
在点P处的切线方程;
(Ⅱ)当a<0时,求函数 的单调递增区间.
的单调递增区间.
(20)(本小题满分12分)
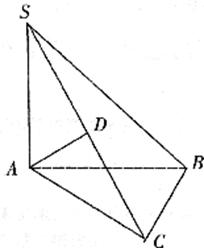
已知△ABC中,∠ACB= ,SA⊥平面ABC,AD⊥SC.
,SA⊥平面ABC,AD⊥SC.
求证:AD上平面SBC.
(21)(本小题满分12分)
某银行准备新设一种定期存款业务,经测算:存款数量与存款利率的平方成正比,比例系数为k(k>0).已知存款利率为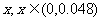 ,贷款利率为4.8%,又银行吸收的存款能全部放贷出去.
,贷款利率为4.8%,又银行吸收的存款能全部放贷出去.
(I)写出存款量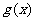 与存款利率
与存款利率 之间的函数关系式;
之间的函数关系式;
(Ⅱ)写出银行应支付给储户的利息 与存款利率
与存款利率 之间的函数关系式;
之间的函数关系式;
(Ⅲ)存款利率为多少时,银行可获得最大利润?(银行利润=贷款数量×贷款利率一存款数量×存款利率)
(22)(本小题满分14分)
已知函数 ,
, ,其定义域都在[0,1]上.
,其定义域都在[0,1]上.
(I)求 的单调区间;
的单调区间;
(Ⅱ)设a≥1,求函数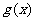 的值域;
的值域;
(1lI)当a≥1时,若对于任意 总存在
总存在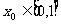 ,使得
,使得 成立,求a的取值范围.
成立,求a的取值范围.
(13)若某物体作 的直线运动,则其在t=1.2s时的瞬时速度______m/s.
的直线运动,则其在t=1.2s时的瞬时速度______m/s.
(14) 设 __________________.
__________________.
(15)已知 ,经计算得:
,经计算得:

由此可推测当n≥2时,有___________________.
(16)一单位关于某种设备的使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
|
x |
2 |
3 |
4 |
5 |
6 |
|
y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
由资料知y对x呈线性相关,而且 ,则线性回归方程是______.
,则线性回归方程是______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com