
3.已知函数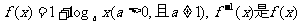 的反函数. 若
的反函数. 若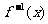 的图象过点(3,4),则a等于 ( )
的图象过点(3,4),则a等于 ( )
A.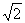 B.
B.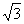 C.
C.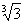 D.2
D.2
|
 {1,2,3},且A的元素中至少含有一个奇数,则满足条件的集合A共有
{1,2,3},且A的元素中至少含有一个奇数,则满足条件的集合A共有
( )
A.6个 B.5个 C.4个 D.3个
2.若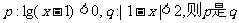 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
(17)(本小题满分12分)
在△ABC中,已知角A、B、C所对的三条边分别是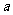 、
、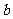 、
、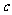 ,且
,且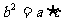
(I)求证: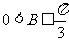 ;
;
(Ⅱ)求函数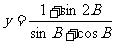 的值域。
的值域。
(18)(本小题满分12分)
已知等比数列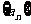 中,
中,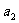 、
、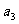 、
、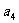 分别是某等差数列的第5项、第3项、第2项,且
分别是某等差数列的第5项、第3项、第2项,且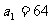 公比
公比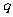 ≠1
≠1
(I)求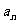
(Ⅱ)设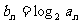 ,求数列
,求数列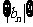 的前
的前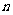 项和
项和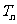 .
.
(19)(本小题满分12分)
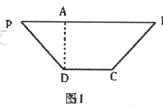
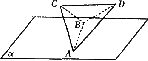
已知等腰梯形PDCB中(如图1),PB=3,DC=1,PD=BC=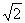 ,A为PB边上一点,且PA=1.将△PAD沿AD折起,使面⊥面ABCD(如图2).
,A为PB边上一点,且PA=1.将△PAD沿AD折起,使面⊥面ABCD(如图2).
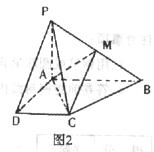
(I)证明:平面PAD⊥平面PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC把几何体分成的两部分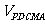 :
: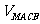 =2:1;
=2:1;
(Ⅲ)在M满足(Ⅱ)的情况下,判断直线PD是否平行平面AMC
(20)(本小题满分12分)
电信局为了配合客户的不同需要,设有A、B两种优惠方案,这两种方案的应付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分)(注:图中MN//CD).试问
(Ⅰ)若通话时间为2小时,按方案A、B各付话费多少元?
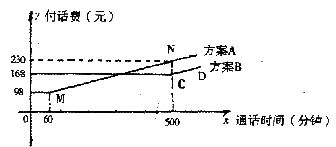
(Ⅱ)方案B从500分钟后,每分钟收费多少元?
(Ⅲ)通话时间在什么范围内,方案B才会比方案A优惠?
(21)(本小题满分12分)
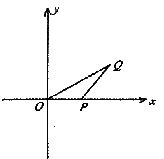
如图,已知△DPQ的面积为S,且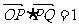 .
.
(Ⅰ)若S∈(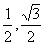 ),求向
),求向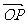 与
与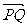 的夹角
的夹角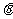 的取值范围;
的取值范围;
(Ⅱ)设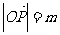 ,S=
,S=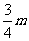 ,以O为中心,P为焦点的椭圆经过点Q,当
,以O为中心,P为焦点的椭圆经过点Q,当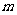 ≥2时,求
≥2时,求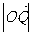 的最小值,并求出此时的椭圆方程.
的最小值,并求出此时的椭圆方程.
(22)(本小题满分14分)
设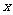 =0是函数
=0是函数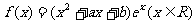 的一个极值点.
的一个极值点.
(Ⅰ)求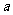 与
与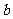 的关系式(用
的关系式(用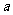 表示
表示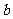 ,并求
,并求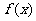 的单调区间;
的单调区间;
(Ⅱ)设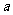 >0,
>0,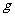 (
(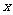 )=
)=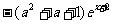 ,问是否存在
,问是否存在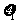 、
、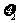 (-2,2),使得
(-2,2),使得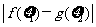 ≤l成立?若存在,求
≤l成立?若存在,求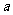 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(13)先后抛掷两枚均匀的正方体骰子,骰子朝上的面的点数为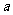 、
、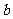 ,则
,则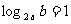 的概率为________。
的概率为________。
(14)从原点向圆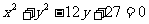 作两条切线,则该圆夹在两条切线间的劣弧长为_______。
作两条切线,则该圆夹在两条切线间的劣弧长为_______。
(15)将函数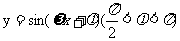 的图象,仅向右平移
的图象,仅向右平移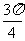 ,或仅向左平移
,或仅向左平移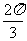 ,所得到的函数图象均关于原点对称,则
,所得到的函数图象均关于原点对称,则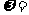 ________________.
________________.
(16)通过观察下述两等式的规律,请你写出一个(包含下面两命题)一般性的命题:
_____________________________________________________________________
①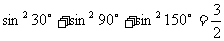 ;②
;②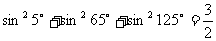
(1)已知复数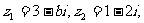 若
若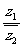 是实数,则实数b的值为
是实数,则实数b的值为
A.
O B. 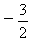 C. 6 D. -6
C. 6 D. -6
(2)已知中心在原点,焦点在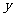 轴上的双曲线的渐近线方程为
轴上的双曲线的渐近线方程为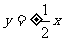 ,则此双曲线的离心率为
,则此双曲线的离心率为
A.
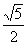 B.
B. 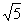 C.
C. 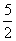 D. 5
D. 5
(3)下列四个命题
①线性相关系数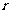 越大,两个变量的线性相关性越强;反之,线性相关性越小;
越大,两个变量的线性相关性越强;反之,线性相关性越小;
②残差平方和越小的模型,拟合的效果越好;
③用相关指数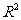 来刻画回归效果,
来刻画回归效果,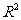 越小,说明模型的拟合效果越好.
越小,说明模型的拟合效果越好.
④随机误差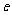 是衡量预报精确度的一个量,它满足
是衡量预报精确度的一个量,它满足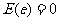 .
.
则正确命题的序号是
A. ①③ B. ②④ C. ①④ D.②③
(4)已知程序框图如右图所示,则该程序框图的功能是
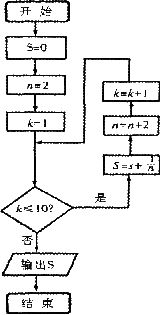
A.
求数列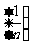 的前10项和(
的前10项和(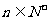 )
)
B.
求数列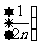 的前10项和(
的前10项和(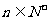 )
)
C.
求数列 的前11项和(
的前11项和(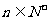 )
)
D.
求数列 的前11项和(
的前11项和(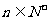 )
)
(5)已知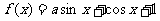 。且
。且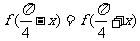 ,则
,则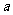 的值为
的值为
A.
1 B. -1 C. 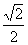 D.
D. 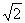
(6)以原点为圆心的圆全部在区域 内,则圆面积的最大值为
内,则圆面积的最大值为
A.
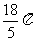 B.
B. 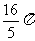 C.
C.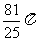 D.
D. 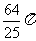
(7)已知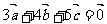 ,且
,且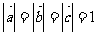 ,则
,则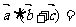
A.
0 B. 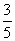 C. -
C. -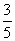 D. -
D. -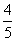
(8)已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图(如图所示),则甲、乙两人得分的中位数之和是
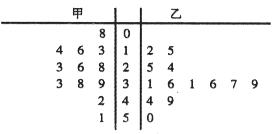
A. 62 B. 63 C.64 D. 65
(9)已知等差数列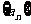 的前
的前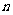 项和为
项和为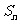 ,若
,若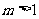 ,且
,且 ,
,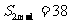 则
则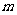 等于
等于
A. 38 B. 20 C.10 D.9
(10)已知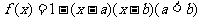 ,
,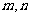 是
是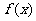 的零点,且
的零点,且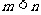 ,则实数
,则实数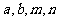 的大小关系是
的大小关系是
A.
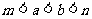 B.
B. 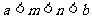
C. 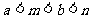 D.
D. 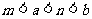
(11)设O为坐标原点,F为抛物线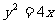 的焦点,A为抛物线上一点,若
的焦点,A为抛物线上一点,若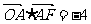 ,则点A的坐标为
,则点A的坐标为
A.
(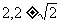 ) B.
(1,±2) C.(1,2)
D.(
) B.
(1,±2) C.(1,2)
D.(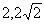 )
)
(12)正四面体ABCD的棱长为1,棱AB//平面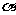 ,则正四面体上的所有点在平面a内的射影构成的图形面积的取值范围是
,则正四面体上的所有点在平面a内的射影构成的图形面积的取值范围是
A.
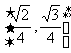 B.
B. 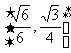 C.
C. 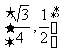 D.
D. 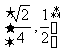
第Ⅱ卷(共90分)
(17)(本小题满分12分)
在△ABC中,已知角A、B、C所对的三条边分别是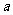 、
、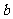 、
、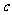 ,且
,且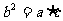
(I)求证: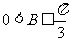 ;
;
(Ⅱ)求函数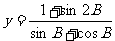 的值域。
的值域。
(18)(本小题满分12分)
已知等比数列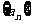 中,
中,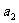 、
、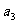 、
、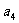 分别是某等差数列的第5项、第3项、第2项,且
分别是某等差数列的第5项、第3项、第2项,且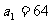 公比
公比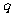 ≠1
≠1
(I)求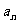
(Ⅱ)设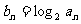 ,求数列
,求数列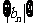 的前
的前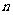 项和
项和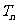 .
.
(19)(本小题满分12分)
已知等腰梯形PDCB中(如图1),PB=3,DC=1,PD=BC=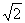 ,A为PB边上一点,且PA=1.将△PAD沿AD折起,使面⊥面ABCD(如图2).
,A为PB边上一点,且PA=1.将△PAD沿AD折起,使面⊥面ABCD(如图2).
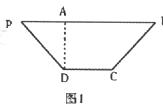
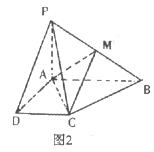
(I)证明:平面PAD⊥平面PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC把几何体分成的两部分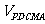 :
: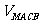 =2:1;
=2:1;
(Ⅲ)在M满足(Ⅱ)的情况下,判断直线PD是否平行平面AMC
(20)(本小题满分12分)
某计算机程序每运行一次都随机出现一个五位的二进制数A=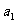
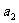
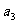
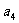
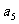 ,其中A的各位数字中,
,其中A的各位数字中,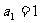 ,
,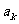 (
(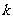 =2,3,4,5)出现的概率为
=2,3,4,5)出现的概率为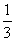 ,出现1的概率为
,出现1的概率为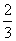 。记
。记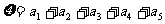 ,当程序运行一次时,
,当程序运行一次时,
(Ⅰ)求 的概率;
的概率;
(Ⅱ)求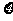 的分布列和数学期望.
的分布列和数学期望.
(21)(本小题满分12分)
已知抛物线C: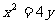 ,的焦点为F,经过点F的直线
,的焦点为F,经过点F的直线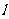 交抛物线于A、B两点,过A、B两点分别作抛物线的切线,设两切线的交点为M
交抛物线于A、B两点,过A、B两点分别作抛物线的切线,设两切线的交点为M
(Ⅰ)求点M的轨迹方程;
(Ⅱ)求证MF⊥AB;
(Ⅲ)设△MAB的面积为S,求S的最小值及此时直线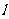 的方程
的方程
(22)(本小题满分14分)
设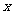 =0是函数
=0是函数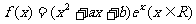 的一个极值点.
的一个极值点.
(I)求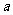 与
与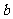 的关系式(用
的关系式(用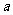 表示
表示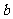 ,并求
,并求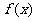 的单调区间;
的单调区间;
(Ⅱ)设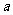 >0,
>0,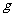 (
(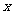 )=
)= ,问是否存在
,问是否存在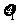 、
、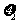 (-2,2),使得
(-2,2),使得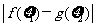 ≤l成立?若存在,求
≤l成立?若存在,求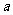 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(13) _____________________.
_____________________.
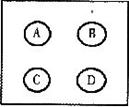
(14)如图,湖中有四个小岛,要在这四个小岛间建三座小桥,使游人可以到达每个小岛,则不同的建法有 种.
(15)将函数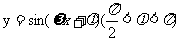 的图象,仅向右平移
的图象,仅向右平移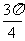 ,或仅向左平移
,或仅向左平移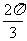 ,所得到的函数图象均关于原点对称,则
,所得到的函数图象均关于原点对称,则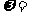 ________________.
________________.
(16)通过观察下述两等式的规律,请你写出一个(包含下面两命题)一般性的命题:
______________________________________________________________________
①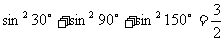 ;②
;②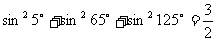
(1)已知复数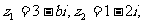 若
若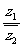 是实数,则实数b的值为
是实数,则实数b的值为
A.
O B. 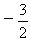 C. 6 D. -6
C. 6 D. -6
(2)已知中心在原点,焦点在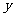 轴上的双曲线的渐近线方程为
轴上的双曲线的渐近线方程为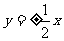 ,则此双曲线的离心率为
,则此双曲线的离心率为
A.
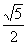 B.
B. 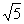 C.
C. 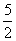 D. 5
D. 5
(3)下列四个命题
①线性相关系数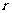 越大,两个变量的线性相关性越强;反之,线性相关性越小;
越大,两个变量的线性相关性越强;反之,线性相关性越小;
②残差平方和越小的模型,拟合的效果越好;
③用相关指数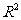 来刻画回归效果,
来刻画回归效果,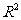 越小,说明模型的拟合效果越好.
越小,说明模型的拟合效果越好.
④随机误差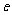 是衡量预报精确度的一个量,它满足
是衡量预报精确度的一个量,它满足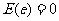 .
.
则正确命题的序号是
A.①③ B. ②④ C. ①④ D. ②③
(4)已知程序框图如右图所示,则该程序框图的功能是
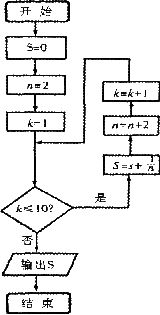
A.
求数列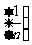 的前10项和(
的前10项和(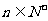 )
)
B.求数列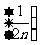 的前10项和(
的前10项和(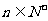 )
)
C.求数列 的前11项和(
的前11项和(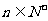 )
)
D.求数列 的前11项和(
的前11项和(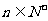 )
)
(5)已知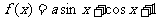 。且
。且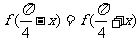 ,则
,则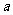 的值为
的值为
A.
1 B. -1 C. 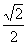 D.
D. 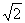
(6)以原点为圆心的圆全部在区域 内,则圆面积的最大值为
内,则圆面积的最大值为
A.
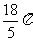 B.
B. 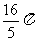 C.
C. 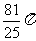 D.
D. 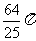
(7)已知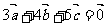 ,且
,且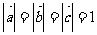 ,则
,则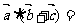
A.
0 B. 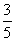 C. -
C. -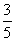 D. -
D. -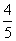
(8)在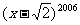 的二项展开式中,含
的二项展开式中,含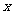 的奇次幂的项之和为
的奇次幂的项之和为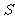 ,当
,当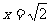 在时,
在时,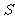 等于
等于
A.
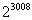 B. -
B. -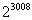 C.
C. 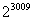 D.-
D.-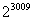
(9)已知等差数列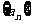 的前
的前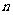 项和为
项和为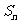 ,若
,若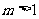 ,且
,且 ,
,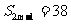 则
则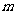 等于
等于
A. 38 B. 20 C. 10 D. 9
(10)已知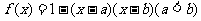 ,
,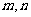 是
是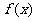 的零点,且
的零点,且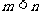 ,则实数
,则实数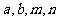 的大小关系是
的大小关系是
A.
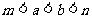 B.
B. 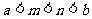
C.
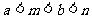 D.
D.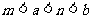
(11)设O为坐标原点,F为抛物线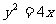 的焦点,A为抛物线上一点,若
的焦点,A为抛物线上一点,若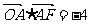 ,则点A的坐标为
,则点A的坐标为
A.
(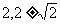 ) B.
(1,±2) C. (1,2)
D. (
) B.
(1,±2) C. (1,2)
D. (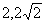 )
)
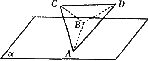
(12)正四面体ABCD的棱长为1,棱AB//平面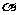 ,则正四面体上的所有点在平面a内的射影构成的图形面积的取值范围是
,则正四面体上的所有点在平面a内的射影构成的图形面积的取值范围是
A.
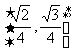 B.
B. 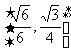 C.
C. 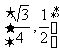 D.
D. 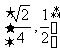
第Ⅱ卷(共90分)
20.(本小题共14分)
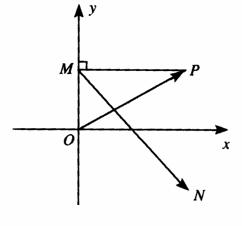
如图,在平面直角坐标系中,已知动点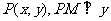 轴,垂足为M,点N与点P关于x轴对称,且
轴,垂足为M,点N与点P关于x轴对称,且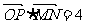
(1)求动点P的轨迹W的方程;
(2)若点Q的坐标为(2,0),A、B为W上的两个动点,且满足QA⊥QB,点Q到直线AB的距离为d,求d的最大值.
19.(本小题共14分)
已知等比数列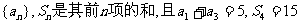
(1)求数列{an}的通项公式;
(2)设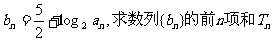
(3)比较(2)中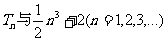 的大小,并说明理由.
的大小,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com