
2.(06年辽宁卷)设+是R上的一个运算, A是R的非空子集,若对任意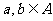 有
有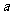 +
+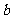
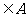 ,则称A对运算+封闭,下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是( )
,则称A对运算+封闭,下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是( )
A.自然数集 B.整数集 C.有理数集 D.无理数集
1.(06年山东)定义集合运算:A⊙B={z︳z= xy(x+y),z∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为( )
A.0 B.6 C.12 D.18
4.(B) 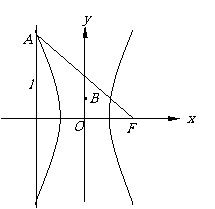 中心在原点的双曲线C1的一个焦点与抛物线C2:y2=8x的焦点F重合,抛物线C2的准线l与双曲线C1的一个交点为A,且|AF|=5.(Ⅰ)求双曲线C1的方程;(Ⅱ)若过点B(0,1)的直线m与双曲线C2相交于不同两点M,N,且((MB=l((BN.①求直线m的斜率k的变化范围;②当直线m的斜率不为0时,问在直线y=x上是否存在一定点C,使((OB^(((CM-l((CN)?若存在,求出点C的坐标;若不存在,请说明理由.
中心在原点的双曲线C1的一个焦点与抛物线C2:y2=8x的焦点F重合,抛物线C2的准线l与双曲线C1的一个交点为A,且|AF|=5.(Ⅰ)求双曲线C1的方程;(Ⅱ)若过点B(0,1)的直线m与双曲线C2相交于不同两点M,N,且((MB=l((BN.①求直线m的斜率k的变化范围;②当直线m的斜率不为0时,问在直线y=x上是否存在一定点C,使((OB^(((CM-l((CN)?若存在,求出点C的坐标;若不存在,请说明理由.
4.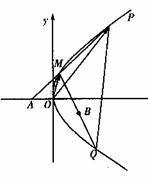 (A)已知椭圆C的中心在原点,焦点在x轴上,一条经过点
(A)已知椭圆C的中心在原点,焦点在x轴上,一条经过点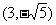 且方向向量为
且方向向量为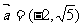 的直线L交椭圆C于A、B两点,交x轴于M点,又
的直线L交椭圆C于A、B两点,交x轴于M点,又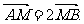
(1)求直线L的方程;
(2)求椭圆C长轴长取值的范围.
3.已知点A(-1,0),B(1,-1)和抛物线.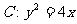 ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
(I)若△POM的面积为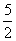 ,求向量
,求向量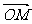 与
与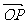 的夹角;
的夹角;
(II)试探求点O到直线PQ的距离是否存在最大值?若存在,求出这个最大值;若不存在,说明理
2.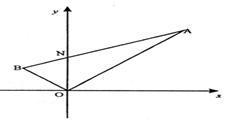 如图,线段AB过y轴上一点N(0,m),AB所在直线的斜率为k(k≠0),两端点A、B到y轴的距离之差为4k。
如图,线段AB过y轴上一点N(0,m),AB所在直线的斜率为k(k≠0),两端点A、B到y轴的距离之差为4k。
(1)求出以y轴为对称轴,过A、O、B三点的抛物线方程;
(2)过抛物线的焦点F作动弦CD,过C、D两点分别作抛物线的切线,设其交点为M,求点M的轨迹方程,并求出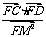 的值。
的值。
1.椭圆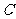 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在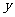 轴上,焦点到相应的准线的距离以及离心率均为
轴上,焦点到相应的准线的距离以及离心率均为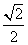 ,直线
,直线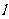 与
与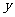 轴交于点
轴交于点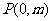 ,与椭圆
,与椭圆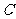 交于相异两点
交于相异两点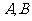 .且
.且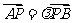 .
.
(1)求椭圆方程; (2)若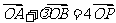 ,求
,求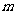 的取值范围.
的取值范围.
5.已知定义在R上的单调函数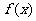 ,存在实数
,存在实数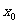 ,使得对于任意实数
,使得对于任意实数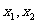 总有
总有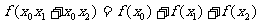 恒成立.(1)求x0的值.(2)若
恒成立.(1)求x0的值.(2)若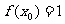 ,且对任意正整数n,有
,且对任意正整数n,有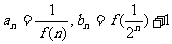 ,记
,记
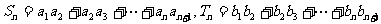 ,比较
,比较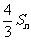 与Tn的大小关系,并给出证明;(3)若不等式
与Tn的大小关系,并给出证明;(3)若不等式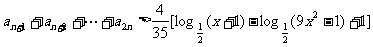 对任意不小于2的正整数n都成立,求x的取值范围.
对任意不小于2的正整数n都成立,求x的取值范围.
4.(A)已知f(x)=ln(1+x2)+ax(a≤0)。
(1)讨论f(x)的单调性。
(2)证明:(1+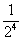 )(1+
)(1+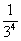 )…(1+
)…(1+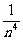 )<e
)<e
(n∈N*,n≥2,其中无理数e=2.71828…)
(B)已知函数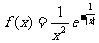
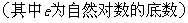
(Ⅰ)判断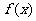 的奇偶性;
的奇偶性;
(Ⅱ)在 上求函数
上求函数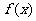 的极值;
的极值;
(Ⅲ)用数学归纳法证明:当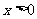 时,对任意正整数
时,对任意正整数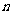 都有
都有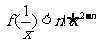
3.已知函数f(x)=ax3+bx2-3x在x=±1处取得极值.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤4;
(Ⅲ)若过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线,求实数m的取值范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com