
4.在等比数列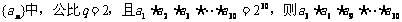 等于( )
等于( )
A.210 B.215 C.216 D.220
3.下列关于函数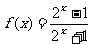 的奇偶性判断正确的为 ( )
的奇偶性判断正确的为 ( )
A.是奇函数但不是偶函数 B.是偶函数但不是奇函数
C.既是奇函数也是偶函数 D.既不是奇函数也不是偶函数
2.若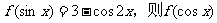 = ( ) A.
= ( ) A.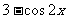 B.
B.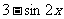 C.
C.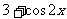 D.
D.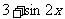
1.用二分法研究函数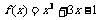 的零点时,第一次经计算
的零点时,第一次经计算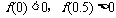 ,可得其中一个零点
,可得其中一个零点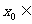 ,第二次应计算 . 以上横线上应填的内容为( )
,第二次应计算 . 以上横线上应填的内容为( )
A.(0,0.5),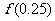 B.(0,1),
B.(0,1),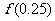
C.(0.5,1),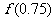 D.(0,0.5),
D.(0,0.5),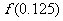
22、(本小题满分14分)
已知函数f(x)=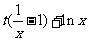 ,t为常数,且t>0。
,t为常数,且t>0。
Ⅰ、若曲线y=f(x)上一点(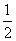 ,y0)处的切线方程为y+2x+ln2-2=0,求t及y0的值;
,y0)处的切线方程为y+2x+ln2-2=0,求t及y0的值;
Ⅱ、若f(x)在区间 上是单调递增函数,求t的取值范围;
上是单调递增函数,求t的取值范围;
Ⅲ、当t=1时,证明: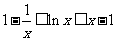 。
。
21、(本小题满分12分)
已知甲袋内有大小相同的2个白球和4个黑球,乙袋内有大小相同的1个白球和3个黑球,现从甲、乙两个袋内各任取2个球。
Ⅰ、求取出的4个球均为黑球的概率;
Ⅱ、求取出的4个球中恰有1个白球的概率;
Ⅲ、设ξ为取出的4个球中白球的个数,求ξ的分布列和数学期望。
20、(本小题满分12分)
在矩形ABCD中,已知AB=1,BC=2.PA⊥平面ABCD,PA=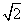 ,Q为BC的中点。
,Q为BC的中点。
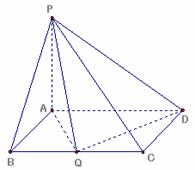
Ⅰ、求证:PQ⊥QD;
Ⅱ、求二面角Q-PD-A的大小。
19、(本小题满分12分)
某种产品的广告费支出x与产品的销售额y之间有如下的对应数据:
|
x(百万元) |
2 |
4 |
5 |
6 |
8 |
|
y(百万元) |
30 |
40 |
60 |
50 |
70 |
Ⅰ、画出上述数据的散点图;
Ⅱ、根据上表提供的数据,求出y关于x的线性回归方程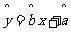 ;
;
Ⅲ、估计广告投入为900万元时的销售额。
18、(本小题满分12分)
Ⅰ、试推导等差数列的前n项和公式;
Ⅱ、设f(x)=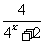 ,类比Ⅰ的推导方法,求f(-9)+f(-8)+…+f(9)+f(10)的值。
,类比Ⅰ的推导方法,求f(-9)+f(-8)+…+f(9)+f(10)的值。
17、(本小题满分12分)
已知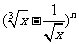 的展开式中,第4项的二项式系数与第5项的二项式系数比为2:5。
的展开式中,第4项的二项式系数与第5项的二项式系数比为2:5。
Ⅰ、求n的值;
Ⅱ、求展开式中含x的项。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com