
4.曲线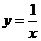 和
和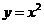 在它们交点处的两条切线与
在它们交点处的两条切线与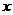 轴所围成的三角形面积是
.
轴所围成的三角形面积是
.
3.对正整数n,设曲线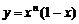 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为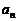 ,则数列
,则数列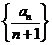 的前n项和的公式是
.
的前n项和的公式是
.
2.过抛物线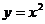 上的点M(
上的点M(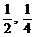 )的切线的倾斜角是
.
)的切线的倾斜角是
.
1.已知函数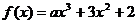 ,f’(-1)=4,则a=
.
,f’(-1)=4,则a=
.
3.已知直线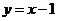 ,点P为y=x2上任意一点,求P在什么位置时到直线距离最短;
,点P为y=x2上任意一点,求P在什么位置时到直线距离最短;
[课堂小结]
[课堂检测]
2.求曲线y=x2过点(0,-1)处的切线方程;
2.求下列函数的导数:
(1) y=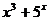 (2)y=
(2)y=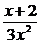
(3)y= 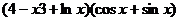 (4)y=
(4)y=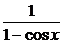
§64 导数的运算(2)
例2.求满足下列条件的函数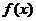
(1)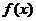 是三次函数,且
是三次函数,且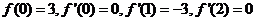
(2)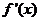 是一次函数,
是一次函数, 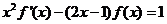
练习:已知函数f(x)=x3+bx2+cx+d的图象过点P(0,2),且在点M处(-1,f(-1))处的切线方程为6x-y+7=0,求函数的解析式
例3.已知点P在函数y=cosx的图象上(0≤x≤2π),在点P处的切线斜率大于0,求点P的横坐标的取值范围.
练习:已知函数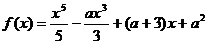 ,且对
,且对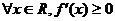 ,
,
求证: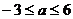
例4.若直线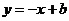 为函数
为函数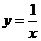 图象的切线,求b的值和切点坐标.
图象的切线,求b的值和切点坐标.
练习:1.求曲线y=x2在点(1,1)处的切线方程;
1.设函数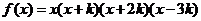 ,且
,且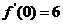 ,则
,则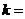 ;
;
1.求下列函数导数.
(1)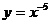 (2)
(2)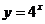 (3)
(3)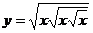
(4)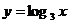 (5)
(5)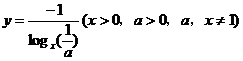
(6)y=sin(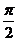 +x)
(7) y=sin
+x)
(7) y=sin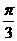 (8)y=cos(2π-x) (9)y=
(8)y=cos(2π-x) (9)y=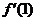
[典型例题讲练]
例1 求下列函数的导数
(1)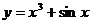 ; (2)
; (2)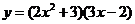 ;(两种方法)
;(两种方法)
(3)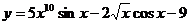 ;(4)y=
;(4)y=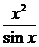 ;.
;.
练习:(1)求y=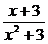 在点x=3处的导数. (2) 求y=
在点x=3处的导数. (2) 求y=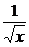 ·cosx的导数.
·cosx的导数.
(3).求y=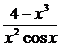 的导数. (4).求
的导数. (4).求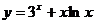 的导数.
的导数.
[课堂小结]
[课堂检测]
2.法则1 两个函数的和(或差)的导数,等于这两个函数的导数的 ,即
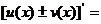 .
.
法则2 常数与函数的积的导数,等于常数与函数的 .
即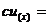 .
.
法则3 两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个函数乘以第二个函数的导数,即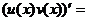 .
.
法则4 两个函数的商的导数,等于 ,即
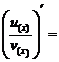
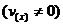 .
.
[基础练习]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com