2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡

皮擦干净后，再选涂其他答案的标号。答在试卷上的答案无效。

第Ⅰ卷

选择题，共12 小题，每小题4 分，共48 分。

12. 解：(Ⅰ)因为，所以有,所以为直角三角形；,则有

所以，,又，,

在中有,即，解得

所求椭圆方程为

(II)

从而将求的最大值转化为求的最大值

是椭圆上的任一点，设，则有即

又，所以

而,所以当时，取最大值,故的最大值为.

11. (3)12

10. 解：(Ⅰ)

因为，所以，当，即时，有最小值0

另法：求导

令，得，此时为增函数；当时，为减函数，

时，有最小值0

(Ⅱ)，得

，，又

，得　

1. 　2. 11　 3. 2 4. 　5. 　6. 7. 　8. 12 9.

12.已知均在椭圆上，直线

、分别过椭圆的左右焦点、，当

时，有.(I)求椭圆的方程;

(II)设P是椭圆上的任一点，为圆的任一条直径，求的最大值.

江苏省泰州中学2010届高三数学基础题训练

(23)答案

11.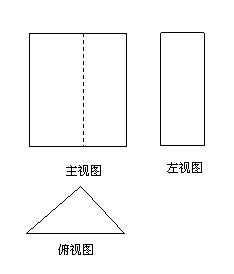已知三棱柱的三视图如图所示，其中主视图和左视图均为矩形，俯视图中，，，．

(1)在三棱柱中，求证：；

(2)在三棱柱中，若是底边的

中点，求证：∥平面；

(3)若三棱柱的高为，求三视图中左视图的面积．

10. 已知向量，函数，

(Ⅰ)求的最小值；(Ⅱ)若，求的值．

9. 定义在R上的奇函数，当x≥0时，则关于的方程

的所有解之和为　　 　　　(用a表示)

8．已知集合，定义函数．若点

、、，的外接圆圆心为，且

，则满足条件的函数有　　　　　 个.