
5.(2004年春季上海,8)根据下列5个图形及相应点的个数的变化规律,试猜测第n个图形中有_________个点.
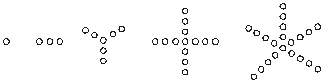
解析:观察图形点分布的变化规律,发现第一个图形只有一个中心点;第二个图形中除中心外还有两边,每边一个点;第三个图形中除中心点外还有三个边,每边两个点;…;依次类推,第n个图形中除中心外有n条边,每边n-1个点,故第n个图形中点的个数为n(n-1)+1.
答案:n2-n+1
●典例剖析
[例1] 比较2n与n2的大小(n∈N *).
剖析:比较两数(或式)大小的常用方法本题不适用,故考虑用归纳法推测大小关系,再用数学归纳法证明.
解:当n=1时,21>12,
当n=2时,22=22,当n=3时,23<32,
当n=4时,24=42,当n=5时,25>52,
猜想:当n≥5时,2n>n2.
下面用数学归纳法证明:
(1)当n=5时,25>52成立.
(2)假设n=k(k∈N *,k≥5)时2k>k2,
那么2k+1=2·2k=2k+2k>k2+(1+1)k>k2+C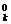 +C
+C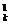 +C
+C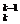 =k2+2k+1=(k+1)
2.
=k2+2k+1=(k+1)
2.
∴当n=k+1时,2n>n2.
由(1)(2)可知,对n≥5的一切自然数2n>n2都成立.
综上,得当n=1或n≥5时,2n>n2;当n=2,4时,2n=n2;当n=3时,2n<n2.
评述:用数学归纳法证不等式时,要恰当地凑出目标和凑出归纳假设,凑目标时可适当放缩.
深化拓展
当n≥5时,要证2n>n2,也可直接用二项式定理证:2n=(1+1)n=C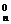 +C
+C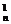 +C
+C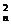 +…+C
+…+C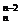 +C
+C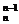 +C
+C >1+n+
>1+n+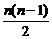 +
+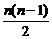 =1+n+n2-n>n2.
=1+n+n2-n>n2.
[例2] 是否存在常数a、b、c使等式1·(n2-12)+2(n2-22)+…+n(n2-n2)=an4+bn2+c对一切正整数n成立?证明你的结论.
剖析:先取n=1,2,3探求a、b、c的值,然后用数学归纳法证明对一切n∈N*,a、b、c所确定的等式都成立.
解:分别用n=1,2,3代入解方程组
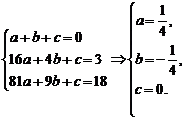
下面用数学归纳法证明.
(1)当n=1时,由上可知等式成立;
(2)假设当n=k+1时,等式成立,
则当n=k+1时,左边=1·[(k+1)2-12]+2[(k+1)2-22]+…+k[(k+1)2-k2]+(k+1)[(k+1)2-(k+1)2]=1·(k2-12)+2(k2-22)+…+k(k2-k2)+1·(2k+1)+2(2k+1)+…+k(2k+1)
=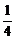 k4+(-
k4+(-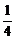 )k2+(2k+1)+2(2k+1)+…+k(2k+1)=
)k2+(2k+1)+2(2k+1)+…+k(2k+1)=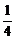 (k+1)4-
(k+1)4-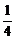 (k+1)2.
(k+1)2.
∴当n=k+1时,等式成立.
由(1)(2)得等式对一切的n∈N*均成立.
评述:本题是探索性命题,它通过观察--归纳--猜想--证明这一完整的思路过程去探索和发现问题,并证明所得结论的正确性,这是非常重要的一种思维能力.
[例3](2003年全国)设a0为常数,且an=3n-1-2an-1(n∈N*).证明:n≥1时,an=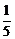 [3n+(-1)n-1·2n]+(-1)n·2n·a0.
[3n+(-1)n-1·2n]+(-1)n·2n·a0.
剖析:给出了递推公式,证通项公式,可用数学归纳法证.
证明:(1)当n=1时,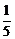 [3+2]-2a0=1-2a0,而a1=30-2a0=1-2a0.
[3+2]-2a0=1-2a0,而a1=30-2a0=1-2a0.
∴当n=1时,通项公式正确.
(2)假设n=k(k∈N*)时正确,即ak=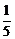 [3k+(-1)k-1·2k]+(-1)k·2k·a0,
[3k+(-1)k-1·2k]+(-1)k·2k·a0,
那么ak+1=3k-2ak=3k-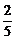 ×3k+
×3k+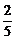 (-1)k·2k+(-1)k+1·2k+1a0
(-1)k·2k+(-1)k+1·2k+1a0
=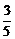 ·3k+
·3k+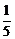 (-1)k·2k+1+(-1)k+1·2k+1·a0
(-1)k·2k+1+(-1)k+1·2k+1·a0
=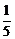 [3k+1+(-1)k·2k+1]+(-1)k+1·2k+1·a0.∴当n=k+1时,通项公式正确.
[3k+1+(-1)k·2k+1]+(-1)k+1·2k+1·a0.∴当n=k+1时,通项公式正确.
由(1)(2)可知,对n∈N*,an=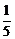 [3n+(-1)n-1·2n]+(-1)n·2n·a0.
[3n+(-1)n-1·2n]+(-1)n·2n·a0.
评述:由n=k正确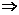 n=k+1时也正确是证明的关键.
n=k+1时也正确是证明的关键.
深化拓展
本题也可用构造数列的方法求an.
解:∵a0为常数,∴a1=3-2a0.
由an=3n-1-2an-1,
得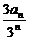 =-
=-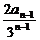 +1,
+1,
即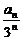 =-
=-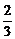 ·
·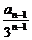 +
+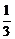 .
.
∴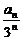 -
-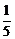 =-
=-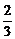 (
(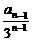 -
-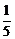 ).
).
∴{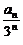 -
-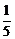 }是公比为-
}是公比为-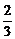 ,首项为
,首项为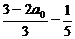 的等比数列.
的等比数列.
∴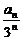 -
-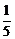 =(
=(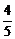 -
-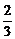 a0)·(-
a0)·(-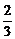 )n-1.
)n-1.
∴an=(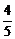 -
-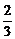 a0)·(-2)n-1×3+
a0)·(-2)n-1×3+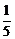 ×3n
×3n
=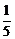 [3n+(-1)n-1·2n]+(-1)n·2n·a0.
[3n+(-1)n-1·2n]+(-1)n·2n·a0.
注:本题关键是转化成an+1=can+d型.
●闯关训练
夯实基础
4.用数学归纳法证明“(n+1)(n+2)·…·(n+n)=2n·1·3·…·(2n-1)”,从“k到k+1”左端需增乘的代数式为
A.2k+1 B.2(2k+1) C.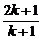 D.
D.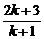
解析:当n=1时,显然成立.
当n=k时,左边=(k+1)(k+2)·…·(k+k),
当n=k+1时,左边=(k+1+1)(k+1+2)·…·(k+1+k)(k+1+k+1)
=(k+2)(k+3)·…·(k+k)(k+1+k)(k+1+k+1)
=(k+1)(k+2)·…·(k+k)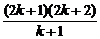 =(k+1)(k+2)·…·(k+k)2(2k+1).
=(k+1)(k+2)·…·(k+k)2(2k+1).
答案:B
3.凸n边形有f(n)条对角线,则凸n+1边形有对角线条数f(n+1)为
A.f(n)+n+1 B.f(n)+n C.f(n)+n-1 D.f(n)+n-2
解析:由n边形到n+1边形,增加的对角线是增加的一个顶点与原n-2个顶点连成的 n-2条对角线,及原先的一条边成了对角线.
答案:C
2.(2004年太原模拟题)若把正整数按下图所示的规律排序,则从2002到2004年的箭头方向依次为
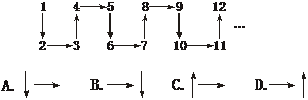
解析:2002=4×500+2,而an=4n是每一个下边不封闭的正方形左、上顶点的数.
答案:D
1.设f(n)=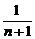 +
+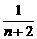 +
+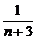 +…+
+…+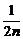 (n∈N *),那么f(n+1)-f(n)等于
(n∈N *),那么f(n+1)-f(n)等于
A.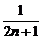 B.
B.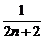
C.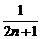 +
+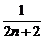 D.
D.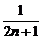 -
-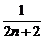
解析:f(n+1)-f(n)=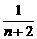 +
+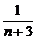 +…+
+…+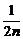 +
+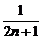 +
+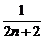 -(
-(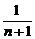 +
+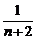 +…+
+…+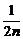 )=
)=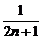 +
+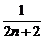 -
-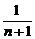 =
=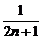 -
-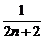 .
.
答案:D
2.数学归纳法的应用:①证恒等式;②整除性的证明;③探求平面几何中的问题;④探求数列的通项;⑤不等式的证明.
特别提示
(1)用数学归纳法证题时,两步缺一不可;
(2)证题时要注意两凑:一凑归纳假设;二凑目标.
●点击双基
1.数学归纳法的定义:由归纳法得到的与自然数有关的数学命题常采用下面的证明方法:(1)先证明当n=n0(n0是使命题成立的最小自然数)时命题成立;(2)假设当n=k(k∈N*, k≥n0)时命题成立,再证明当n=k+1时命题也成立,那么就证明这个命题成立,这种证明方法叫数学归纳法.
13.1 数学归纳法
●知识梳理
1.数学归纳法、极限
要求:(1)理解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题.
(2)了解数列极限和函数极限的概念.
(3)掌握极限的四则运算法则,会求某些数列与函数的极限.
(4)了解函数连续的意义,理解闭区间上连续函数有最大值和最小值的性质.
●复习方略指南
极限的概念和方法是近代数学的核心内容,微积分学的基本概念、基本方法在现代实践中越来越多的被应用,并在现代数学及相关学科的研究中不断得到进一步的发展.本章的主要内容由两部分组成,一是数学归纳法,二是极限.学习极限时要注意数列极限和函数极限的联系和区别、函数的极限与函数连续性的渐进性.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com