
2.指数函数
(1)指数函数的定义
一般地,函数y=ax(a>0且a≠1)叫做指数函数.
(2)指数函数的图象
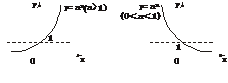
底数互为倒数的两个指数函数的图象关于y轴对称.
(3)指数函数的性质
①定义域:R.
②值域:(0,+∞).
③过点(0,1),即x=0时,y=1.
④当a>1时,在R上是增函数;当0<a<1时,在R上是减函数.
●点击双基
1.指数
(1)n次方根的定义
若xn=a,则称x为a的n次方根,“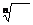 ”是方根的记号.
”是方根的记号.
在实数范围内,正数的奇次方根是一个正数,负数的奇次方根是一个负数,0的奇次方根是0;正数的偶次方根是两个绝对值相等符号相反的数,0的偶次方根是0,负数没有偶次方根.
(2)方根的性质
①当n为奇数时,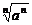 =a.
=a.
②当n为偶数时,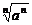 =|a|=
=|a|=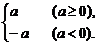
(3)分数指数幂的意义
①a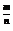 =
=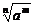 (a>0,m、n都是正整数,n>1).
(a>0,m、n都是正整数,n>1).
②a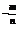 =
=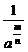 =
=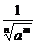 (a>0,m、n都是正整数,n>1).
(a>0,m、n都是正整数,n>1).
2.7 指数与指数函数
●知识梳理
4.二次函数与二次不等式密切相关,借助二次函数的图象和性质,可方便直观地解决与不等式有关的问题.例如:
(1)二次不等式f(x)=ax2+bx+c≤0的解集是(-∞,α]∪[β,+∞)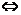 a<0且f(α)=f(β)=0.
a<0且f(α)=f(β)=0.
(2)当a>0时,f(α)<f(β)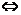 |α+
|α+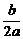 |<|β+
|<|β+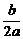 |;
|;
当a<0时,f(α)<f(β)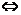 |α+
|α+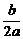 |>|β+
|>|β+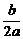 |.
|.
(3)当a>0时,二次不等式f(x)>0在[p,q]上恒成立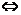
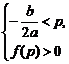 或
或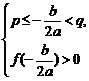 或
或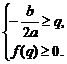
(4)f(x)>0恒成立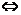
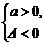 或
或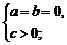
f(x)<0恒成立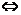
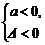 或
或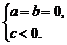
拓展题例
[例1] 已知当m∈R时,函数f(x)=m(x2-1)+x-a的图象和x轴恒有公共点,求实数a的取值范围.
解:(1)m=0时,f(x)=x-a是一次函数,它的图象恒与x轴相交,此时a∈R.
(2)m≠0时,由题意知,方程mx2+x-(m+a)=0恒有实数解,其充要条件是Δ=1+4m(m+a)=4m2+4am+1≥0.又只需Δ′=(4a)2-16≤0,解得-1≤a≤1,即a∈[-1,1].
∴m=0时,a∈R;
m≠0时,a∈[-1,1].
评述:g(a)是a的函数,可作出g(a)的草图来求最大值.
[例2] 已知f(x)=ax2+bx+c的图象过点(-1,0),是否存在常数a、b、c,使不等式x≤f(x)≤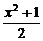 对一切实数x都成立?
对一切实数x都成立?
解:∵f(x)的图象过点(-1,0), ∴a-b+c=0 ①
∵x≤f(x)≤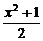 对一切x∈R均成立,
对一切x∈R均成立,
∴当x=1时也成立,即1≤a+b+c≤1.
故有a+b+c=1. ②
由①②得b=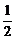 ,c=
,c=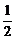 -a. ∴f(x)=ax2+
-a. ∴f(x)=ax2+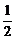 x+
x+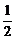 -a.
-a.
故x≤ax2+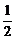 x+
x+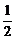 -a≤
-a≤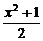 对一切x∈R成立,
对一切x∈R成立,
也即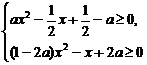 恒成立
恒成立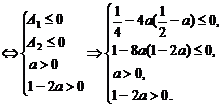
解得a=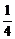 .∴c=
.∴c=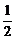 -a=
-a=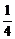 .
.
∴存在一组常数a=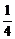 ,b=
,b=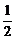 ,c=
,c=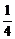 ,使不等式x≤f(x)≤
,使不等式x≤f(x)≤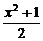 对一切实数x均成立.
对一切实数x均成立.
评述:赋值法(特殊值法)可以使“探索性”问题变得比较明朗,它是解决这类问题比较常用的方法.
3.结合图象可以得到一系列与二次方程ax2+bx+c=0(a≠0)的根的分布有关的结论,教学时可引导学生总结:
(1)方程f(x)=0的两根中一根比r大,另一根比r小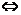 a·f(r)<0.
a·f(r)<0.
(2)二次方程f(x)=0的两根都大于r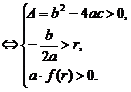
(3)二次方程f(x)=0在区间(p,q)内有两根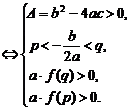
(4)二次方程f(x)=0在区间(p,q)内只有一根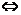 f(p)·f(q)<0,或f(p)=0,另一根在(p,q)内或f(q)=0,另一根在(p,q)内.
f(p)·f(q)<0,或f(p)=0,另一根在(p,q)内或f(q)=0,另一根在(p,q)内.
(5)方程f(x)=0的两根中一根大于p,另一根小于q(p<q)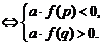
2.求二次函数的解析式就是确定函数式f(x)=ax2+bx+c(a≠0)中a、b、c的值.二次函数也可以表示为y=a(x-x0)2+h或y=a(x-x1)(x-x2)(b2-4ac≥0)等形式,应提醒学生根据题设条件选用适当的表示形式,用待定系数法确定相应字母的值.
1.二次函数是最重要的初等函数之一,因为很多问题可化归为二次函数来处理,所以必须熟练掌握二次函数的性质,并能灵活运用这些性质去解决问题.
2.二次函数、一元二次方程和一元二次不等式是一个有机的整体,要深刻理解它们相互之间的关系,能用函数思想来研究方程和不等式,便是抓住了关键.
●教师下载中心
教学点睛
1.二次函数f(x)=ax2+bx+c的图象形状、对称轴、顶点坐标、开口方向等是处理二次函数问题的重要依据.
9.二次函数f(x)=px2+qx+r中实数p、q、r满足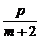 +
+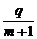 +
+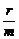 =0,其中m>0,
=0,其中m>0,
求证:(1)pf(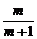 )<0;
)<0;
(2)方程f(x)=0在(0,1)内恒有解.
证明:(1)pf(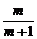 )=p[p(
)=p[p(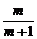 )2+q(
)2+q(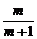 )+r]
)+r]
=pm[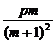 +
+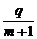 +
+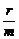 ]
]
=pm[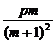 -
-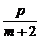 ]
]
=p2m[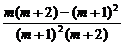 ]
]
=p2m[-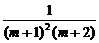 ].
].
由于f(x)是二次函数,故p≠0.
又m>0,所以pf(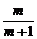 )<0.
)<0.
(2)由题意,得f(0)=r,f(1)=p+q+r.
①当p>0时,由(1)知f(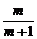 )<0.
)<0.
若r>0,则f(0)>0,又f(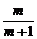 )<0,
)<0,
∴f(x)=0在(0,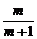 )内有解;
)内有解;
若r≤0,则f(1)=p+q+r=p+(m+1)(-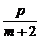 -
-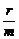 )+r=
)+r=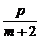 -
-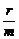 >0,
>0,
又f(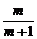 )<0,
)<0,
所以f(x)=0在(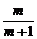 ,1)内有解.
,1)内有解.
因此方程f(x)=0在(0,1)内恒有解.
②当p<0时,同样可以证得结论.
评述:(1)题目点明是“二次函数”,这就暗示着二次项系数p≠0,若将题中的“二次”两个字去掉,所证结论相应更改.
(2)对字母p、r分类时先对哪个分类是有一定讲究的.本题的证明中,先对p分类,然后对r分类显然是比较好的.
●思悟小结
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com