
5.已知f(x)=2ax-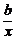 +lnx在x=-1,x=
+lnx在x=-1,x=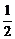 处取得极值.
处取得极值.
(1)求a、b的值;
(2)若对x∈[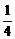 ,4]时,f(x)>c恒成立,求c的取值范围.
,4]时,f(x)>c恒成立,求c的取值范围.
解:(1)∵f(x)=2ax-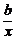 +lnx,
+lnx,
∴f′(x)=2a+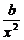 +
+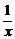 .
.
∵f(x)在x=-1与x=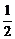 处取得极值,
处取得极值,
∴f′(-1)=0,f′(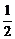 )=0,
)=0,
即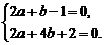 解得
解得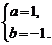
∴所求a、b的值分别为1、-1.
(2)由(1)得f′(x)=2-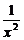 +
+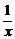 =
=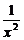 (2x2+x-1)=
(2x2+x-1)=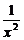 (2x-1)(x+1).
(2x-1)(x+1).
∴当x∈[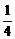 ,
,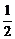 ]时,f′(x)<0;当x∈[
]时,f′(x)<0;当x∈[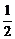 ,4]时,f′(x)>0.∴f(
,4]时,f′(x)>0.∴f(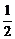 )是f(x)在[
)是f(x)在[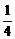 ,4]上的极小值.又∵只有一个极小值,
,4]上的极小值.又∵只有一个极小值,
∴f(x)min=f(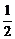 )=3-ln2.
)=3-ln2.
∵f(x)>c恒成立,∴c<f(x)min=3-ln2.
∴c的取值范围为c<3-ln2.
4.(2005年北京东城区模拟题)如果函数y=f(x)的导函数的图象如下图所示,给出下列判断:
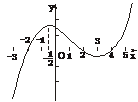
①函数y=f(x)在区间(-3,-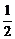 )内单调递增;
)内单调递增;
②函数y=f(x)在区间(-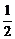 ,3)内单调递减;
,3)内单调递减;
③函数y=f(x)在区间(4,5)内单调递增;
④当x=2时,函数y=f(x)有极小值;
⑤当x=-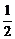 时,函数y=f(x)有极大值.
时,函数y=f(x)有极大值.
则上述判断中正确的是_____________
解析:当x∈(4,5)时,恒有f′(x)>0.
答案:③
3.函数y=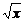 -2x(x≥0)的最大值为_____________.
-2x(x≥0)的最大值为_____________.
解析:y′=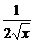 -2,
-2,
当0<x<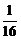 时,y′>0,∴y=
时,y′>0,∴y=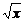 -2x在(0,
-2x在(0,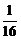 )上为增函数.
)上为增函数.
当x>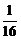 时,y′<0,∴y=
时,y′<0,∴y=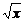 -2x在(
-2x在(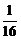 ,+∞)上是减函数.∴y=
,+∞)上是减函数.∴y=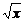 -2x在(0,+∞)上的最大值为
-2x在(0,+∞)上的最大值为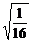 -
-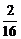 =
=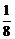 .
.
答案: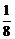
2.函数f(x)=sin(3x-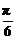 )在点(
)在点(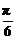 ,
,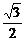 )处的切线方程是
)处的切线方程是
A.3x+2y+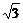 -
-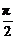 =0
=0
B.3x-2y+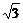 -
-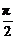 =0
=0
C.3x-2y-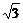 -
-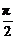 =0
=0
D.3x+2y-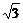 -
-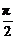 =0
=0
解析:因为f′(x)=3cos(3x-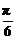 ),所以所求切线的斜率为f′(
),所以所求切线的斜率为f′(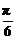 )=
)=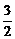 ,切线方程为y-
,切线方程为y-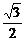 =
=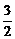 (x-
(x-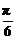 ),即3x-2y+
),即3x-2y+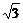 -
-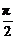 =0.
=0.
答案:B
1.下列各式正确的是
A.x-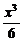 >sinx (x>0)
>sinx (x>0)
B.sinx<x (x>0)
C.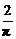 x>sinx (0<x<
x>sinx (0<x<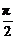 )
)
D.以上各式都不对
解析:令F(x)=x-sinx,则F′(x)=1-cosx>0(当x>0,x≠2nπ,n=1,2,…).
故F(x)在x>0时单调递增.因此当x>0时,有F(x)>F(0)=0.
答案:B
5.若函数f(x)=x3+x2+mx+1是R上的单调递增函数,则m的取值范围是______________
_____________________.
解析:f′(x)=3x2+2x+m.∵f(x)在R上是单调递增函数,
∴f′(x)>0在R上恒成立,
即3x2+2x+m>0.
由Δ=4-4×3m<0,得m>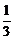 .
.
答案:m>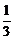
●典例剖析
[例1] 求函数y=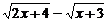 的值域.
的值域.
剖析:求函数值域是中学数学中的难点,一般可以通过图象观察或利用不等式性质来求解,也可以利用函数的单调性求出值域.本题形式结构复杂,可采用求导的方法求解.
解:函数的定义域由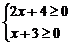 求得x≥-2.
求得x≥-2.
求导得y′=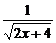 -
-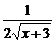
=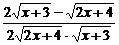 .
.
由y′>0得2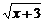 >
>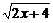 ,
,
即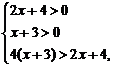 解得x>-2,即函数y=
解得x>-2,即函数y=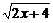 -
-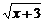 在(-2,+∞)上是增函数.
在(-2,+∞)上是增函数.
又此函数在x=-2处连续,∴在[-2,+∞)上是增函数,而f(-2)=-1.
∴函数y=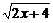 -
-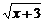 的值域是[-1,+∞).
的值域是[-1,+∞).
评述:函数y=f(x)在(a,b)上为单调函数,当在[a,b]上连续时,y=f(x)在[a,b]上也是单调函数.
[例2] 已知f(x)=ax3+bx2+cx(a≠0)在x=±1时取得极值,且f(1)=-1,
(1)试求常数a、b、c的值;
(2)试判断x=±1是函数的极大值还是极小值,并说明理由.
剖析:考查函数f(x)是实数域上的可导函数,可先求导确定可能的极值点,再通过极值点与导数的关系,即极值点必为f′(x)=0的根建立起由极值点x=±1所确定的相关等式,运用待定系数法确定a、b、c的值.
(1)解法一:f′(x)=3ax2+2bx+c,∵x=±1是函数的极值点,
∴x=±1是方程3ax2+2bx+c=0的两根.
由根与系数的关系知
又f(1)=-1,∴a+b+c=-1. ③
由①②③解得a=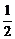 ,b=0,c=-
,b=0,c=-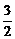 .
.
解法二:由f′(1)=f′(-1)=0,
得3a+2b+c=0, ①
3a-2b+c=0. ②
又f(1)=-1,∴a+b+c=-1. ③
由①②③解得a=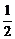 ,b=0,c=-
,b=0,c=-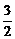 .
.
(2)解:f(x)=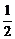 x3-
x3-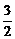 x,∴f′(x)=
x,∴f′(x)=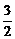 x2-
x2-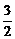 =
=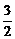 (x-1)(x+1).
(x-1)(x+1).
当x<-1或x>1时,f′(x)>0;当-1<x<1时,f′(x)<0.
∴x=-1时,f(x)有极大值;x=1时,f(x)有极小值.
[例3] 已知函数f(x)=2ax-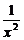 ,x∈(0,1].
,x∈(0,1].
(1)若f(x)在x∈(0,1]上是增函数,求a的取值范围;
(2)求f(x)在区间(0,1]上的最大值.
剖析:(1)要使f(x)在(0,1]上为增函数,需f′(x)>0,x∈(0,1).
(2)利用函数的单调性求最大值.
解:(1)由已知可得f′(x)=2a+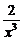 ,∵f(x)在(0,1)上是增函数,∴f′(x)>0,即a>-
,∵f(x)在(0,1)上是增函数,∴f′(x)>0,即a>-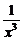 , x∈(0,1].∴a>-1.
, x∈(0,1].∴a>-1.
当a=-1时,f′(x)=-2+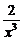 对x∈(0,1)也有f′(x)>0,满足f(x)在(0,1]上为增函数,
对x∈(0,1)也有f′(x)>0,满足f(x)在(0,1]上为增函数,
∴a≥-1.
(2)由(1)知,当a≥-1时,f(x)在(0,1]上为增函数,
∴[f(x)]max=f(1)=2a-1.
当a<-1时,令f′(x)=0得x=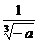 ,
,
∵0<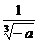 <1,∴0<x<
<1,∴0<x<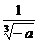 时,f′(x)>0;
时,f′(x)>0;
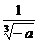 <x≤1时,f′(x)<0.∴f(x)在(0,
<x≤1时,f′(x)<0.∴f(x)在(0, 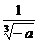 )上是增函数,在(
)上是增函数,在(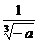 ,1]减函数.
,1]减函数.
∴[f(x)]max=f (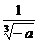 )=-3
)=-3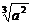 .
.
评述:求参数的取值范围,凡涉及函数的单调性、最值问题时,用导数的知识解决较简单.
深化拓展
(1)也可用函数单调性的定义求解.
思考讨论
函数f(x)在区间D上的极值与最值有什么联系?
●闯关训练
夯实基础
4.函数f(x)=ex+e-x在(0,+∞)上的单调性是__________.
解析:∵f′(x)=ex-e-x=e-x(e2x-1),∴当x∈(0,+∞)时,f′(x)>0.
∴f(x)在(0,+∞)上是增函数.
答案:增函数
3.设f(x)在(a,b)内有定义,x0∈(a,b),当x<x0时,f′(x)>0;当x>x0时,f′(x)<0.则x0是
A.间断点 B.极小值点
C.极大值点 D.不一定是极值点
解析:f(x)在x0处不一定连续.
答案:D
2.函数y=1+3x-x3有
A.极小值-2,极大值2
B.极小值-2,极大值3
C.极小值-1,极大值1
D.极小值-1,极大值3
解析:y′=3-3x2=3(1+x)(1-x).
令y′=0得x1=-1,x2=1.当x<-1时,y′<0,函数y=1+3x-x3是减函数;当-1<x<1时, y′>0,函数y=1+3x-x3是增函数;当x>1时,y′<0,函数y=1+3x-x3是减函数.
∴当x=-1时,函数y=1+3x-x3有极小值-1;当x=1时,函数y=1+3x-x3有极大值3.
答案:D
1.(2005年海淀区高三第一学期期末模拟)函数y=xsinx+cosx在下面哪个区间内是增函数
A.(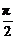 ,
,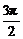 )
B.(π,2π)
)
B.(π,2π)
C.(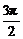 ,
, 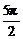 )
D.(2π,3π)
)
D.(2π,3π)
解析:y′=(xsinx+cosx)′=sinx+xcosx-sinx=xcosx,
当x∈(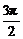 ,
,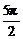 )时,恒有xcosx>0.
)时,恒有xcosx>0.
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com