3.两种抽样方法的比较(略).

2.分层抽样：当已知总体由差异明显的几部分组成时，为了使样本更充分地反映总体的情况，常将总体分成几部分，然后按照各部分所占的比进行抽样，这种抽样叫做分层抽样.

1.简单随机抽样：一般地，设一个总体的个体数为N，如果通过逐个抽取的方法从中抽取一个样本，且每次抽取时各个个体被抽到的概率相等，就称这样的抽样为简单随机抽样.

12.1　 抽样方法与总体分布的估计

●知识梳理

3.会用样本估计总体平均值和方差.

●复习方略指南

在本章的复习中，要理解几种抽样方法的区别与联系.应充分注意一些重要概念的实际意义，理解概率统计中处理问题的基本思想方法，掌握所学的概率统计知识的实际应用.

这部分内容高考命题趋向主要以选择题、填空题为主，重点考查基础知识、基本概念及其简单的应用.

对有关概率统计的应用题要多加关注.

2.会用样本频率分布估计总体分布.

1.了解简单随机抽样、分层抽样及系统抽样的意义，会用它们对简单实际问题进行抽样.

4.n次独立重复试验中某事件发生k次的概率P_n(k)=C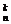p^k(1－p)^n－k正好是二项式［(1－p)+p］ⁿ的展开式的第k+1项.

拓展题例

[例1] 把n个不同的球随机地放入编号为1，2，…，m的m个盒子内，求1号盒恰有r个球的概率.

解法一：用独立重复试验的概率公式.把1个球放入m个不同的盒子内看成一次独立试验，其中放入1号盒的概率为P=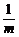.这样n个球放入m个不同的盒子内相当于做n次独立重复试验.由独立重复试验中事件A恰好发生k次的概率公式知，1号盒恰有r个球的概率

P_n(r)=C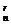p^r(1－p)^n－r=C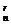·(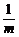)^r·(1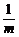－)^n－r=.

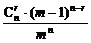解法二：用古典概型.把n个不同的球任意放入m个不同的盒子内共有mⁿ个等可能的结果.其中1号盒内恰有r个球的结果数为C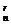(m－1)^n－r，故所求概率P(A)=.

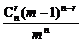答：1号盒恰有r个球的概率为.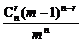

[例2] 假设每一架飞机引擎在飞行中故障率为1－P，且各引擎是否故障是独立的，如果至少50%的引擎能正常运行，飞机就可以成功地飞行，问对于多大的P而言，4引擎飞机比2引擎的飞机更为安全？

分析：4引擎飞机可以看作4次独立重复试验，要能正常运行，即求发生k次(k≥2)的概率.同理，2引擎飞机正常运行的概率即是2次独立重复试验中发生k次(k≥1)的概率，由此建立不等式求解.

解：4引擎飞机成功飞行的概率为

C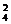P²(1－P)²+C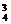P³(1－P)+C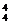P⁴=6P²(1－P)²+4P³(1－P)+P⁴.

2引擎飞机成功飞行的概率为C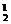P(1－P)+C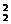P²=2P(1－P)+P².

要使4引擎飞机比2引擎飞机安全，只要6P²(1－P)²+4P³(1－P)+P⁴≥2P(1－P)+P².

化简，分解因式得(P－1)²(3P－2)≥0.

所以3P－2≥0，

即得P≥.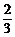

答：当引擎不出故障的概率不小于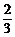时，4引擎飞机比2引擎飞机安全.

3.某些事件若含有较多的互斥事件，可考虑其对立事件的概率，这样可减少运算量，提高正确率.要注意“至多”“至少”等题型的转化，如例1.

2.A、B中至少有一个发生：A+B.

(1)若A、B互斥：P(A+B)=P(A)+P(B)，否则不成立.

(2)若A、B相互独立(不互斥).

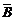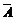法一：P(A+B)=P(A·B)+P(A·)+P(·B)；

法二：P(A+B)=1－P(·)；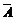

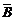法三：P(A+B)=P(A)+P(B)－P(AB).