
8.(理)(2003年重庆市高三毕业班诊断性考试)某市有小灵通与全球通两种手机,小灵通手机的月租费为25元,接听电话不收费,打出电话一次在3 min以内收费0.2元,超过3 min的部分为每分钟收费0.1元,不足1 min按1 min计算(以下同).全球通手机月租费为10元,接听与打出的费用都是每分钟0.2元.若某人打出与接听次数一样多,每次接听与打出的时间在1 min以内、1到2 min以内、2到3 min以内、3到4 min以内的次数之比为4∶3∶1∶1.问,根据他的通话次数应该选择什么样的手机才能使费用最省?(注:m到m+1 min以内指含m min,而不含m+1 min)
解:设小灵通每月的费用为y1元,全球通的费用为y2元,分别在1 min以内、2 min以内、3 min以内、4 min以内的通话次数为4x、3x、x、x,则
y1=25+(4x+3x+x+x)×0.2+0.1x=25+1.9x,
y2=10+2(0.2×4x+0.4×3x+0.6x+0.8x)=10+6.8x.
令y1≥y2,即25+1.9x≥10+6.8x,
解得x≤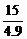 ≈3.06.
≈3.06.
∴总次数为(4+3+1+1)×2×3.06=55.1.
故当他每月的通话次数小于等于55次时,应选择全球通,大于55次时应选择小灵通.
(文)(2005年北京东城区模拟题)定义“符号函数”f(x)=sgnx=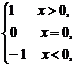 则不等式x+2>(x-2)sgnx的解集是______________.
则不等式x+2>(x-2)sgnx的解集是______________.
解析:分类讨论.
答案:(-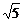 ,+∞)
,+∞)
探究创新
7.设f(x)=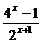 -2x+1,已知f(m)=
-2x+1,已知f(m)=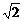 ,求f(-m).
,求f(-m).
解:∵f(m)=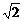 ,∴
,∴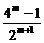 -2m+1=
-2m+1=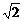 . ①
. ①
∴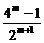 -2m=
-2m=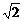 -1.
-1.
而f(-m)=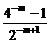 +2m+1=
+2m+1=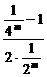 +2m+1=
+2m+1=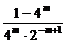 +2m+1=
+2m+1=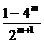 +2m+1=-
+2m+1=-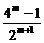 + 2m+1=-(
+ 2m+1=-(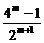 -2m)+1=-(
-2m)+1=-(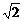 -1)+1=2-
-1)+1=2-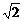 .
.
6.设定义在N上的函数f(x)满足f(n)=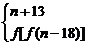
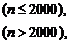 试求f(2002)的值.
试求f(2002)的值.
解:∵2002>2000,
∴f(2002)=f[f(2002-18)]=f[f(1984)]=f[1984+13]=f(1997)=1997+13=2010.
5.(2005年北京市西城区模拟题)已知函数f(x)=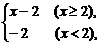 则f(lg30-lg3)=___________________;不等式xf(x-1)<10的解集是___________________.
则f(lg30-lg3)=___________________;不等式xf(x-1)<10的解集是___________________.
解析:f(lg30-lg3)=f(lg10)=f(1)=-2,
f(x-1)=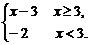
当x≥3时,x(x-3)<10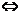 -2<x<5,故3≤x<5.
-2<x<5,故3≤x<5.
当x<3时,-2x<10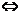 x>-5,故-5<x<3.
x>-5,故-5<x<3.
总之x∈(-5,5).
答案:-2 {x|-5<x<5}
培养能力
4.用长为l的铁丝弯成下部为矩形,上部为半圆形的框架(如下图),若矩形底边长为2x,求此框架围成的面积y与x的函数关系式,并写出其定义域.
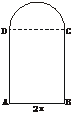
解:∵AB=2x,则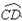 =πx,AD=
=πx,AD=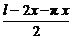 .
.
∴y=2x·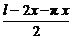 +
+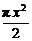 =-(
=-(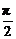 +2)x2+lx.
+2)x2+lx.
由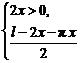 >0,解得0<x<
>0,解得0<x<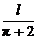 .
.
3.已知f(x2-4)=lg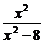 ,则f(x)的定义域为__________.
,则f(x)的定义域为__________.
解析:设x2-4=t,则t≥-4,x2=4+t.
∴f(t)=lg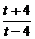 .∴f(x)=lg
.∴f(x)=lg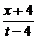 (x≥-4).
(x≥-4).
由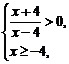 得x>4.
得x>4.
答案:(4,+∞)
2.如果f[f(x)]=2x-1,则一次函数f(x)=___________________.
解析:设f(x)=kx+b,则f[f(x)]=kf(x)+b=k(kx+b)+b=k2x+kb+b.
由于该函数与y=2x-1是同一个函数,
∴k2=2且kb+b=-1.∴k=±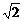 .
.
当k=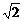 时,b=1-
时,b=1-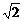 ;
;
当k=-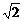 时,b=1+
时,b=1+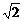 .
.
答案:f(x)=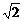 x+1-
x+1-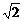 或f(x)=-
或f(x)=-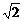 x+1+
x+1+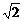
1.函数y=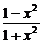 的值域是
的值域是
A.[-1,1] B.(-1,1] C.[-1,1) D.(-1,1)
解法一:y=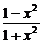 =
=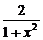 -1.∵1+x2≥1,
-1.∵1+x2≥1,
∴0<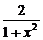 ≤2.∴-1<y≤1.
≤2.∴-1<y≤1.
解法二:由y=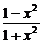 ,得x2=
,得x2=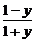 .
.
∵x2≥0,∴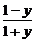 ≥0,解得-1<y≤1.
≥0,解得-1<y≤1.
解法三:令x=tanθ(-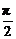 <θ<
<θ<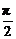 ),则y=
),则y=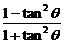 =cos2θ.∵-π<2θ<π,
=cos2θ.∵-π<2θ<π,
∴-1<cos2θ≤1,即-1<y≤1.
答案:B
4.函数y=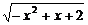 的定义域为______________,值域为___________________.
的定义域为______________,值域为___________________.
答案:[-1,2]
[0,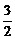 ]
]
●典例剖析
[例1] 已知函数f(x)=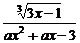 的定义域是R,则实数a的取值范围是
的定义域是R,则实数a的取值范围是
A.a>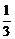 B.-12<a≤0 C.-12<a<0 D.a≤
B.-12<a≤0 C.-12<a<0 D.a≤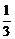
剖析:由a=0或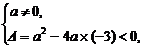 可得-12<a≤0.
可得-12<a≤0.
答案:B
[例2] 在△ABC中,BC=2,AB+AC=3,中线AD的长为y,AB的长为x,建立y与x的函数关系式,并指出其定义域.
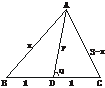
解:设∠ADC=θ,则∠ADB=π-θ.
根据余弦定理得
12+y2-2ycosθ=(3-x)2, ①
12+y2-2ycos(π-θ)=x2. ②
由①+②整理得y=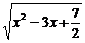 .
.
其中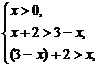 解得
解得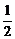 <x<
<x<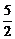 .
.
∴函数的定义域为(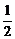 ,
,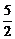 ).
).
评述:函数的定义域是使式子有意义的自变量的取值范围,同时也要注意变量的实际意义的要求.
[例3] 若函数f(x)=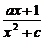 的值域为[-1,5],求实数a、c.
的值域为[-1,5],求实数a、c.
解:由y=f(x)=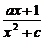 ,得x2y-ax+cy-1=0.
,得x2y-ax+cy-1=0.
当y=0时,ax=-1,∴a≠0.
当y≠0时,∵x∈R,∴Δ=a2-4y(cy-1)≥0.
∴4cy2-4y-a2≤0.∵-1≤y≤5,∴-1、5是方程4cy2-4y-a2=0的两根.
∴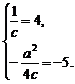 ∴
∴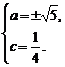
评述:求f(x)=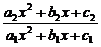 (a12+a22≠0)的值域时,常利用函数的定义域非空这一隐含的条件,将函数转化为方程,利用Δ≥0转化为关于函数值的不等式.求解时,要注意二次项系数为字母时要讨论.
(a12+a22≠0)的值域时,常利用函数的定义域非空这一隐含的条件,将函数转化为方程,利用Δ≥0转化为关于函数值的不等式.求解时,要注意二次项系数为字母时要讨论.
●闯关训练
夯实基础
3.(2005年春季北京,文2)函数f(x)=|x-1|的图象是
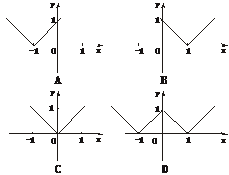
解析:转化为分段函数y=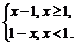
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com