
5.(2004年上海,19)记函数f(x)=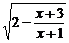 的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域为B.
的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域为B.
(1)求A;
(2)若B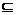 A,求实数a的取值范围.
A,求实数a的取值范围.
解:(1)由2-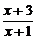 ≥0,得
≥0,得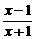 ≥0,
≥0,
∴x<-1或x≥1,即A=(-∞,-1)∪[1,+∞).
(2)由(x-a-1)(2a-x)>0,得(x-a-1)(x-2a)<0.
∵a<1,∴a+1>2a.∴B=(2a,a+1).
∵B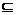 A,∴2a≥1或a+1≤-1,即a≥
A,∴2a≥1或a+1≤-1,即a≥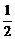 或a≤-2.
或a≤-2.
而a<1,∴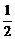 ≤a<1或a≤-2.
≤a<1或a≤-2.
故当B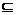 A时,实数a的取值范围是(-∞,-2]∪[
A时,实数a的取值范围是(-∞,-2]∪[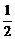 ,1).
,1).
培养能力
4.已知关于x的方程sin2x-2sinx-a=0有实数解,求a的取值范围.
解:a=sin2x-2sinx=(sinx-1)2-1.
∵-1≤sinx≤1,∴0≤(sinx-1)2≤4.
∴a的范围是[-1,3].
3.(2003年春季北京)若存在常数p>0,使得函数f(x)满足f(px)=f(px-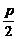 )(x∈R),则f(x)的一个正周期为__________.
)(x∈R),则f(x)的一个正周期为__________.
解析:由f(px)=f(px-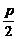 ),
),
令px=u,f(u)=f(u-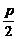 )=f[(u+
)=f[(u+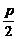 )-
)-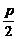 ],∴T=
],∴T=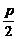 或
或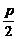 的整数倍.
的整数倍.
答案: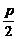 (或
(或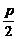 的整数倍)
的整数倍)
2.(2003年郑州市质检题)关于x的方程|x2-4x+3|-a=0有三个不相等的实数根,则实数a的值是___________________.
解析:作函数y=|x2-4x+3|的图象,如下图.
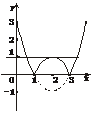
由图象知直线y=1与y=|x2-4x+3|的图象有三个交点,即方程|x2-4x+3|=1也就是方程|x2-4x+3|-1=0有三个不相等的实数根,因此a=1.
答案:1
1.已知y=f(x)在定义域[1,3]上为单调减函数,值域为[4,7],若它存在反函数,则反函数在其定义域上
A.单调递减且最大值为7 B.单调递增且最大值为7
C.单调递减且最大值为3 D.单调递增且最大值为3
解析:互为反函数的两个函数在各自定义区间上有相同的增减性,f-1(x)的值域是[1,3].
答案:C
2.(2003年郑州市质检题)若f(x)是R上的减函数,且f(x)的图象经过点A(0,3)和B(3,-1),则不等式|f(x+1)-1|<2的解集是___________________.
解析:由|f(x+1)-1|<2得-2<f(x+1)-1<2,即-1<f(x+1)<3.
又f(x)是R上的减函数,且f(x)的图象过点A(0,3),B(3,-1),
∴f(3)<f(x+1)<f(0).
∴0<x+1<3,-1<x<2.
答案:(-1,2)
●典例剖析
[例1] 取第一象限内的点P1(x1,y1),P2(x2,y2),使1,x1,x2,2依次成等差数列,1,y1,y2,2依次成等比数列,则点P1、P2与射线l:y=x(x>0)的关系为
A.点P1、P2都在l的上方 B.点P1、P2都在l上
C.点P1在l的下方,P2在l的上方 D.点P1、P2都在l的下方
剖析:x1=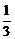 +1=
+1=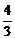 ,x2=1+
,x2=1+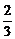 =
=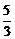 ,y1=1×
,y1=1×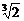 =
=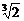 ,y2=
,y2=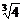 ,∵y1<x1,y2<x2,
,∵y1<x1,y2<x2,
∴P1、P2都在l的下方.
答案:D
[例2] 已知f(x)是R上的偶函数,且f(2)=0,g(x)是R上的奇函数,且对于x∈R,都有g(x)=f(x-1),求f(2002)的值.
解:由g(x)=f(x-1),x∈R,得f(x)=g(x+1).又f(-x)=f(x),g(-x)=-g(x),
故有f(x)=f(-x)=g(-x+1)=-g(x-1)=-f(x-2)=-f(2-x)=-g(3-x)=
g(x-3)=f(x-4),也即f(x+4)=f(x),x∈R.
∴f(x)为周期函数,其周期T=4.
∴f(2002)=f(4×500+2)=f(2)=0.
评述:应灵活掌握和运用函数的奇偶性、周期性等性质.
[例3] 函数f(x)=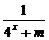 (m>0),x1、x2∈R,当x1+x2=1时,f(x1)+f(x2)=
(m>0),x1、x2∈R,当x1+x2=1时,f(x1)+f(x2)=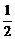 .
.
(1)求m的值;
(2)数列{an},已知an=f(0)+f(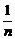 )+f(
)+f(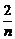 )+…+f(
)+…+f(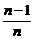 )+f(1),求an.
)+f(1),求an.
解:(1)由f(x1)+f(x2)=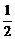 ,得
,得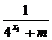 +
+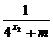 =
=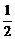 ,
,
∴4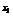 +4
+4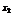 +2m=
+2m=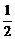 [4
[4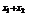 +m(4
+m(4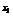 +4
+4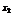 )+m2].
)+m2].
∵x1+x2=1,∴(2-m)(4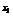 +4
+4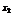 )=(m-2)2.
)=(m-2)2.
∴4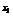 +4
+4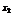 =2-m或2-m=0.
=2-m或2-m=0.
∵4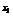 +4
+4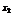 ≥2
≥2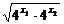 =2
=2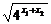 =4,
=4,
而m>0时2-m<2,∴4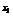 +4
+4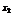 ≠2-m.
≠2-m.
∴m=2.
(2)∵an=f(0)+f(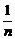 )+f(
)+f(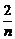 )+…+f(
)+…+f(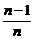 )+f(1),∴an=f(1)+f(
)+f(1),∴an=f(1)+f(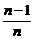 )+ f(
)+ f(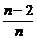 )+…+f(
)+…+f(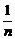 )+f(0).
)+f(0).
∴2an=[f(0)+f(1)]+[f(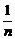 )+f(
)+f(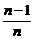 )]+…+[f(1)+f(0)]=
)]+…+[f(1)+f(0)]=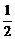 +
+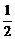 +…+
+…+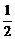 =
=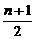 .
.
∴an=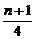 .
.
深化拓展
用函数的思想处理方程、不等式、数列等问题是一重要的思想方法.
[例4] 函数f(x)的定义域为R,且对任意x、y∈R,有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,f(1)=-2.
(1)证明f(x)是奇函数;
(2)证明f(x)在R上是减函数;
(3)求f(x)在区间[-3,3]上的最大值和最小值.
(1)证明:由f(x+y)=f(x)+f(y),得f[x+(-x)]=f(x)+f(-x),∴f(x)+ f(-x)=f(0).又f(0+0)=f(0)+f(0),∴f(0)=0.从而有f(x)+f(-x)=0.
∴f(-x)=-f(x).∴f(x)是奇函数.
(2)证明:任取x1、x2∈R,且x1<x2,则f(x1)-f(x2)=f(x1)-f[x1+(x2-x1)]=f(x1)-[f(x1)+f(x2-x1)]=-f(x2-x1).由x1<x2,∴x2-x1>0.∴f(x2-x1)<0.
∴-f(x2-x1)>0,即f(x1)>f(x2),从而f(x)在R上是减函数.
(3)解:由于f(x)在R上是减函数,故f(x)在[-3,3]上的最大值是f(-3),最小值是f(3).由f(1)=-2,得f(3)=f(1+2)=f(1)+f(2)=f(1)+f(1+1)=f(1)+f(1)+f(1)=3f(1)=3×(-2)=-6,f(-3)=-f(3)=6.从而最大值是6,最小值是-6.
深化拓展
对于任意实数x、y,定义运算x*y=ax+by+cxy,其中a、b、c是常数,等式右边的运算是通常的加法和乘法运算.现已知1*2=3,2*3=4,并且有一个非零实数m,使得对于任意实数x,都有x*m=x,试求m的值.
提示:由1*2=3,2*3=4,得
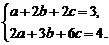
∴b=2+2c,a=-1-6c.
又由x*m=ax+bm+cmx=x对于任意实数x恒成立,
∴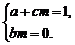 ∴b=0=2+2c.
∴b=0=2+2c.
∴c=-1.∴(-1-6c)+cm=1.
∴-1+6-m=1.∴m=4.
答案:4.
●闯关训练
夯实基础
1.已知函数f(x)=lg(2x-b)(b为常数),若x∈[1,+∞)时,f(x)≥0恒成立,则
A.b≤1 B.b<1 C.b≥1 D.b=1
解析:当x∈[1,+∞)时,f(x)≥0,从而2x-b≥1,即b≤2x-1.而x∈[1,+∞)时,2x-1单调增加,
∴b≤2-1=1.
答案:A
3.函数与实际应用问题的综合.
●点击双基
2.函数与其他数学知识点的综合,如方程、不等式、数列、解析几何等方面的内容与函数的综合.这是高考主要考查的内容.
1.函数内容本身的相互综合,如函数概念、性质、图象等方面知识的综合.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com