
4.从图中的12个点中任取3个点作为一组,其中可构成三角形的组数是

A.208 B.204 C.200 D.196
解析:在12个点中任取3个点的组合数为C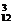 ,在同一直线上的3点的组数为20,则可构成三角形的组数为C
,在同一直线上的3点的组数为20,则可构成三角形的组数为C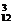 -20=200.
-20=200.
答案:C
3.从1到10的正整数中,任意抽取两个相加,所得和为奇数的不同情形有__________种.
解析:当且仅当偶数加上奇数后和为奇数,从而不同情形有5×5=25种.
答案:25
2.(2004年黄冈检测题)某班新年联欢会原定的6个节目已排成节目单,开演前又增加了3个新节目,如果将这3个节目插入节目单中,那么不同的插法种数为
A.504 B.210 C.336 D.120
解析:三个新节目一个一个插入节目单中,分别有7、8、9种方法.
∴插法种数为7×8×9=504或A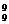 ÷A
÷A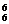 =504.
=504.
答案:A
1.(2004年全国,文5)从长度分别为1、2、3、4的四条线段中,任取三条的不同取法共有n种.在这些取法中,以取出的三条线段为边可组成的三角形的个数为m,则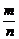 等于
等于
A.0 B.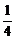 C.
C.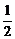 D.
D.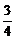
解析:n=C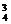 =4,在“1、2、3、4”这四条线段中,由三角形的性质“两边之和大于第三边,两边之差小于第三边”知可组成三角形的有“2、3、4”,m=1.∴
=4,在“1、2、3、4”这四条线段中,由三角形的性质“两边之和大于第三边,两边之差小于第三边”知可组成三角形的有“2、3、4”,m=1.∴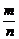 =
= 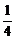 .
.
答案:B
5.(2005年春季北京,13)从-1,0,1,2这四个数中选三个不同的数作为函数f(x)=ax2+bx+c的系数,可组成不同的二次函数共有_____________个,其中不同的偶函数共有_____________个.(用数字作答)
解析:一个二次函数对应着a、b、c(a≠0)的一组取值,a的取法有3种,b的取法有3种,c的取法有2种,由分步计数原理,知共有二次函数3×3×2=18个.
若二次函数为偶函数,则b=0.
同上共有3×2=6个.
答案:18 6
●典例剖析
[例1] 电视台在“欢乐今宵”节目中拿出两个信箱,其中存放着先后两次竞猜中成绩优秀的观众来信,甲信箱中有30封,乙信箱中有20封.现由主持人抽奖确定幸运观众,若先确定一名幸运之星,再从两信箱中各确定一名幸运伙伴,有多少种不同的结果?
解:分两类:(1)幸运之星在甲箱中抽,再在两箱中各定一名幸运伙伴,有30×29×20=17400种结果;(2)幸运之星在乙箱中抽,同理有20×19×30=11400种结果.因此共有17400+11400=28800种不同结果.
评述:在综合运用两个原理时,既要合理分类,又要合理分步,一般情况是先分类再分步.
思考讨论
本题为什么要先分类?由于幸运之星在哪个信箱产生对幸运伙伴的产生有影响,分步计数原理中步与步间要独立.
[例2] 从集合{1,2,3,…,10}中,选出由5个数组成的子集,使得这5个数中的任何两个数的和不等于11,这样的子集共有多少个?
解:和为11的数共有5组:1与10,2与9,3与8,4与7,5与6,子集中的元素不能取自同一组中的两数,即子集中的元素取自5个组中的一个数.而每个数的取法有2种,
所以子集的个数为2×2×2×2×2=25=32.
评述:解本题的关键是找出和为11的5组数,然后再用分步计数原理求解.
深化拓展
上例中选出5个数组成子集改为选出4个数呢?
答案:C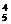 ·24=80个.
·24=80个.
[例3] (2003年新课程卷)某城市在中心广场建造一个花圃,花圃分为6个部分(如下图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有_____________种.(以数字作答)
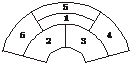
解法一:从题意来看6部分种4种颜色的花,又从图形看知必有2组同颜色的花,从同颜色的花入手分类求.
(1)②与⑤同色,则③⑥也同色或④⑥也同色,所以共有N1=4×3×2×2×1=48种;
(2)③与⑤同色,则②④或⑥④同色,所以共有N2=4×3×2×2×1=48种;
(3)②与④且③与⑥同色,则共有N3=4×3×2×1=24种.
所以,共有N=N1+N2+N3=48+48+24=120种.
解法二:记颜色为A、B、C、D四色,先安排1、2、3有A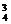 种不同的栽法,不妨设1、2、3已分别栽种A、B、C,则4、5、6栽种方法共5种,由以下树状图清晰可见.
种不同的栽法,不妨设1、2、3已分别栽种A、B、C,则4、5、6栽种方法共5种,由以下树状图清晰可见.
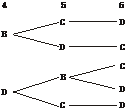
根据分步计数原理,不同栽种方法有N=A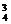 ×5=120.
×5=120.
答案:120
评述:解法一是常规解法,解法二安排4、5、6时又用了分类和列举的方法.
●闯关训练
夯实基础
4.72的正约数(包括1和72)共有__________个.
解析:72=23×32.
∴2m·3n(0≤m≤3,0≤n≤2,m,n∈N)都是72的正约数.
m的取法有4种,n的取法有3种,由分步计数原理共3×4个.
答案:12
3.某城市的电话号码,由六位升为七位(首位数字均不为零),则该城市可增加的电话部数是
A.9×8×7×6×5×4×3 B.8×96
C.9×106 D.81×105
解析:电话号码是六位数字时,该城市可安装电话9×105部,同理升为七位时为9×106.∴可增加的电话部数是9×106-9×105=81×105.
答案:D
2.(2002年全国)从正方体的6个面中选取3个面,其中有2个面不相邻的选法共有
A.8种 B.12种 C.16种 D.20种
解析:有2个面不相邻即有一组对面,所以选法为C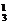 ·C
·C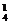 =12种.
=12种.
答案:B
1.十字路口来往的车辆,如果不允许回头,共有_____________种行车路线.
A.24 B.16 C.12 D.10
解析:起点为C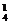 种可能性,终点为C
种可能性,终点为C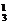 种可能性,因此,行车路线共有C
种可能性,因此,行车路线共有C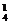 ×C
×C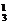 =12种.
=12种.
答案:C
10.1 分类计数原理、分步计数原理
●知识梳理
分类计数原理与分步计数原理是计数问题的基本原理,它贯穿于全章学习的始终,体现了解决问题时将其分解的两种常用方法,即把问题分类解决和分步解决,是本章学习的重点.
特别提示
正确区分和使用两个原理是学好本章的关键,其核心是“完成一件事”是“分类”完成,还是“分步”完成.
●点击双基
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com