
12.2 总体期望值和方差的估计
●知识梳理
4.处理有关离散型随机变量的应用问题,关键在于根据实际问题确定恰当的随机变量.
●教师下载中心
教学点睛
离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率和.
求离散型随机变量的分布列必须解决好两个问题,一是求出ξ的所有取值,二是求出ξ取每一个值时的概率.
求一些离散型随机变量的分布列,在某种程度上就是正确地求出相应的事件个数,即相应的排列组合数,所以学好排列组合是学好分布列的基础与前提.
拓展题例
[例题] 盒中装有一打(12个)乒乓球,其中9个新的,3个旧的(用过的球即为旧的),从盒中任取3个使用,用完后装回盒中,此时盒中旧球个数ξ是一个随机变量,求ξ的分布列.
剖析:从盒中任取3个,这3个可能全是旧的,2个旧的1个新的,1个旧的2个新的或全是新的,所以用完放回盒中,盒中旧球个数可能是3个,4个,5个,6个,即ξ可以取3,4,5,6.
解:ξ的所有可能取值为3,4,5,6.
P(ξ=3)=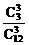 =
=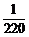 ;
;
P(ξ=4)=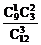 =
=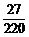 ;
;
P(ξ=5)=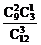 =
=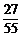 ;
;
P(ξ=6)=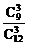 =
=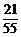 .
.
所以ξ的分布列为
|
ξ |
3 |
4 |
5 |
6 |
|
P |
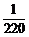 |
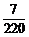 |
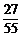 |
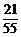 |
评述:本题的关键是正确地求出ξ取某个值时对应的事件个数.
思考讨论
若本题改为:若每次取1个,用完放回再取1个,用完再放回,再取1个用完放回,则怎样求此时ξ的分布列呢?
3.离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和.
2.求离散型随机变量的分布列,首先要根据具体情况确定ξ的取值情况,然后利用排列、组合与概率知识求出ξ取各个值的概率.
1.离散型随机变量的概率分布的两个本质特征:pi≥0(i=1,2,…,n)与 pi=1是确定分布列中参数值的依据.
pi=1是确定分布列中参数值的依据.
9.如果ξ-B(20,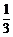 ),则使P(ξ=k)取最大值的k的值是________.
),则使P(ξ=k)取最大值的k的值是________.
解析: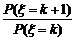 =
=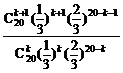 =
=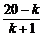 ×
×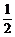 ≥1,
≥1,
得k≤6.
所以当k≤6时,P(ξ=k+1)≥P(ξ=k),
当k>0时,P(ξ=k+1)<P(ξ=k),
其中k=6时,P(ξ=k+1)=P(ξ=k),
从而k=6或7时,P(ξ=k)取得最大值.
答案:6或7
●思悟小结
8.一袋中装有5只球,编号为1,2,3,4,5,在袋中同时取3只,以ξ表示取出的3只球中的最大号,写出随机变量ξ的分布列.
解:根据题意可知随机变量ξ的取值为3,4,5.
当ξ=3时,即取出的三只球中最大号码为3,则其他两球的编号只能是1,2,故有P(ξ=3)=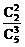 =
=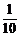 .
.
当ξ=4时,即取出的三只球中最大号码为4,则其他两球只能在编号为1,2,3的3球中取2个,故P(ξ=4)=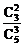 =
=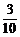 .
.
P(ξ=5)=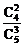 =
=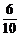 .
.
可得ξ的分布列为
|
ξ |
3 |
4 |
5 |
|
P |
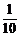 |
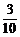 |
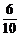 |
探究创新
7.金工车间有10台同类型的机床,每台机床配备的电动机功率为10 kW,已知每台机床工作时,平均每小时实际开动12 min,且开动与否是相互独立的.现因当地电力供应紧张,供电部门只提供50 kW的电力,这10台机床能够正常工作的概率为多大?在一个工作班的8 h内,不能正常工作的时间大约是多少?
分析:由实际问题确定随机变量的取值,由独立重复试验求概率值.
解:设10台机床中实际开动的机床数为随机变量ξ,由于机床类型相同,且机床的开动与否相互独立,因此ξ-B(10,p).其中p是每台机床开动的概率,由题意p=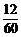 =
=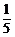 .从而P(ξ=k)=C
.从而P(ξ=k)=C (
(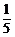 )k(
)k(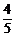 )10-k,k=0,1,2,…,10.
)10-k,k=0,1,2,…,10.
50 kW电力同时供给5台机床开动,因而10台机床同时开动的台数不超过5台时都可以正常工作.这一事件的概率为P(ξ≤5),
P(ξ≤5)=C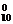 (
(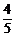 )10+C
)10+C ·
·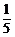 ·(
·(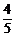 )9+C
)9+C (
(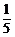 )2·(
)2·(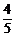 )8+C
)8+C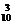 (
(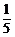 )3(
)3(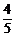 )7+C
)7+C (
(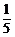 )4·(
)4·(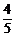 )6+C
)6+C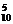 (
(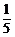 )5·(
)5·(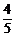 )5≈0.994.
)5≈0.994.
因此,在电力供应为50 kW的条件下,机床不能正常工作的概率仅约为0.006,从而在一个工作班的8 h内,不能正常工作的时间只有大约8×60×0.006=2.88(min),这说明,10台机床的工作基本上不受电力供应紧张的影响.
评述:分布列的实际应用,应结合题意给出答案.
6.(2003年高考·新课程)A、B两个代表队进行乒乓球对抗赛,每队三名队员,A队队员是A1、A2、A3,B队队员是B1、B2、B3,按以往多次比赛的统计,对阵队员之间胜负概率如下:
|
对阵队员 |
A队队员胜的概率 |
A队队员负的概率 |
|
A1对B1 |
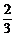 |
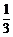 |
|
A2对B2 |
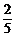 |
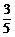 |
|
A3对B3 |
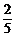 |
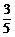 |
现按表中对阵方式出场,每场胜队得1分,负队得0分.设A队、B队最后所得总分分别为ξ、η.
(1)求ξ、η的概率分布;
(2)求Eξ、Eη.
分析:本题考查离散型随机变量分布列和数学期望等概念,考查运用概率知识解决实际问题的能力.
解:(1)ξ、η的可能取值分别为3,2,1,0.
P(ξ=3)=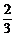 ×
×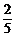 ×
×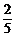 =
= ,
,
P(ξ=2)=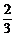 ×
×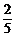 ×
×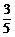 +
+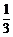 ×
×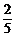 ×
×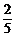 +
+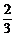 ×
×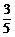 ×
×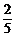 =
=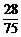 ,
,
P(ξ=1)=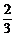 ×
×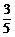 ×
×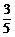 +
+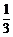 ×
×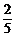 ×
×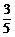 +
+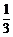 ×
×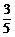 ×
×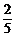 =
=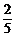 ,
,
P(ξ=0)=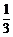 ×
×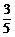 ×
×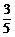 =
=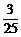 ;
;
根据题意知ξ+η=3,所以
P(η=0)=P(ξ=3)= ,
,
P(η=1)=P(ξ=2)=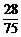 ,
,
P(η=2)=P(ξ=1)=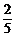 ,
,
P(η=3)=P(ξ=0)=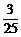 .
.
(2)Eξ=3× +2×
+2×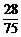 +1×
+1×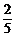 +0×
+0×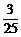 =
=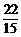 ;
;
因为ξ+η=3,
所以Eη=3-Eξ= .
.
5.(2004年天津,理18)从4名男生和2名女生中任选3人参加演讲比赛.设随机变量ξ表示所选3人中女生的人数.
(1)求ξ的分布列;
(2)求ξ的数学期望;
(3)求“所选3人中女生人数ξ≤1”的概率.
解:(1)ξ的可能取值为0,1,2.
P(ξ=k)=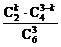 ,k=0,1,2.
,k=0,1,2.
∴ξ的分布列为
|
ξ |
0 |
1 |
2 |
|
P |
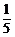 |
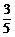 |
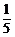 |
(2)由(1),可知
Eξ=0×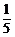 +1×
+1×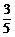 +2×
+2×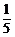 =1.
=1.
(3)“所选3人中女生人数ξ≤1”的概率为
P(ξ≤1)=P(ξ=0)+P(ξ=1)=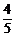 .
.
培养能力
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com