
1.椭圆的定义是解决问题的出发点,尤其是第二定义,如果运用恰当可收到事半功倍之效(如关于求焦半径的问题).
9.已知常数a>0,在矩形ABCD中,AB=4,BC=4a, O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且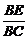 =
=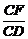 =
=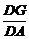 ,P为GE与OF的交点(如下图).问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
,P为GE与OF的交点(如下图).问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
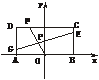
分析:根据题设条件首先求出P点坐标满足的方程,据此可判断是否存在两点,使得点P到两定点距离的和为定值.
解:按题意,有A(-2,0),B(2,0),C(2,4a),D(-2,4a).
设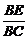 =
=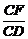 =
=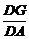 =k(0≤k≤1),
=k(0≤k≤1),
由此有E(2,4ak),F(2-4k,4a),G(-2,4a-4ak).
直线OF的方程为2ax+(2k-1)y=0. ①
直线GE的方程为-a(2k-1)x+y-2a=0. ② 由①②消去参数k,
得点P(x,y)满足方程2a2x2+y2-2ay=0.
整理得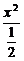 +
+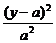 =1.
=1.
当a2=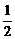 时,点P的轨迹为圆弧,所以不存在符合题意的两点.
时,点P的轨迹为圆弧,所以不存在符合题意的两点.
当a2≠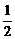 时,点P的轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长.
时,点P的轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长.
当a2<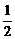 时,点P到椭圆两个焦点(-
时,点P到椭圆两个焦点(-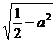 ,a),(
,a),(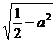 ,a)的距离之和为定值
,a)的距离之和为定值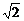 .
.
当a2>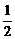 时,点P到椭圆两个焦点(0,a-
时,点P到椭圆两个焦点(0,a-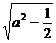 ),(0,a+
),(0,a+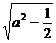 )的距离之和为定值2a.
)的距离之和为定值2a.
评注:本题主要考查根据已知条件求轨迹的方法,椭圆的方程和性质,利用方程判定曲线的性质,曲线与方程关系等解析几何的基本思想和综合解题能力.在解题过程中蕴涵着方程思想、分类讨论思想和构造法.
●思悟小结
8.(2003年南京市模拟题)设x、y∈R,i、j为直角坐标平面内x、y轴正方向上的单位向量,若向量a=xi+(y+2)j,b=xi+(y-2)j,且|a|+|b|=8.
(1)求点M(x,y)的轨迹C的方程.
(2)过点(0,3)作直线l与曲线C交于A、B两点,设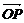 =
=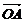 +
+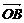 ,是否存在这样的直线l,使得四边形OAPB是矩形?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使得四边形OAPB是矩形?若存在,求出直线l的方程;若不存在,试说明理由.
(1)解法一:∵a=xi+(y+2)j,b=xi+(y-2)j,且|a|+|b|=8,
∴点M(x,y)到两个定点F1(0,-2),F2(0,2)的距离之和为8.
∴轨迹C为以F1、F2为焦点的椭圆,方程为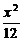 +
+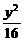 =1.
=1.
解法二:由题知,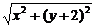 +
+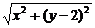 =8,
=8,
移项,得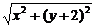 =8-
=8-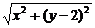 ,
,
两边平方,得
x2+(y+2)2=x2+(y-2)2-16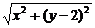 +64,
+64,
整理,得2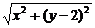 =8-y,
=8-y,
两边平方,得4[x2+(y-2)2]=(8-y)2,
展开,整理得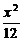 +
+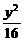 =1.
=1.
(2)∵l过y轴上的点(0,3),
若直线l是y轴,则A、B两点是椭圆的顶点.
∵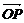 =
=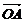 +
+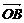 =0,
=0,
∴P与O重合,与四边形OAPB是矩形矛盾.
∴直线l的斜率存在.设l方程为y=kx+3,A(x1,y1),B(x2,y2),
|
|
 y=kx+3,
y=kx+3,
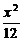 +
+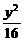 =1,
=1,
(-21)>0恒成立,且x1+x2=-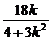 ,x1x2=-
,x1x2=-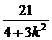 .
.
∵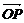 =
=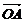 +
+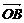 ,∴四边形OAPB是平行四边形.若存在直线l,使得四边形OAPB是矩形,则OA⊥OB,即
,∴四边形OAPB是平行四边形.若存在直线l,使得四边形OAPB是矩形,则OA⊥OB,即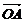 ·
·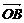 =0.
=0.
∵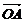 =(x1,y1),
=(x1,y1),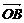 =(x2,y2),
=(x2,y2),
∴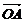 ·
·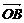 =x1x2+y1y2=0,
=x1x2+y1y2=0,
即(1+k2)x1x2+3k(x1+x2)+9=0,
即(1+k2)·(-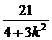 )+3k·(-
)+3k·(-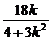 )+9=0,即k2=
)+9=0,即k2=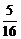 ,得k=±
,得k=±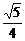 .
.
∴存在直线l:y=±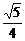 x+3,使得四边形OAPB是矩形.
x+3,使得四边形OAPB是矩形.
探究创新
7.已知椭圆的中心在坐标原点O,焦点在坐标轴上,直线y=x+1与椭圆相交于点P和点Q,且OP⊥OQ,|PQ|=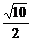 ,求椭圆方程.
,求椭圆方程.
解:设椭圆方程为mx2+ny2=1(m>0,n>0),
设P(x1,y1),Q(x2,y2),解方程组
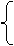 y=x+1,
y=x+1,
mx2+ny2=1.
消去y,整理得(m+n)x2+2nx+n-1=0.
Δ=4n2-4(m+n)(n-1)>0,即m+n-mn>0,OP⊥OQ x1x2+y1y2=0,
x1x2+y1y2=0,
即x1x2+(x1+1)(x2+1)=0,2x1x2+(x1+x2)+1=0,∴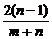 -
-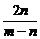 +1=0.
+1=0.
∴m+n=2. ①
由弦长公式得2·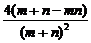 =(
=(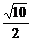 )2,将m+n=2代入,得m·n=
)2,将m+n=2代入,得m·n=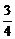 . ②
. ②
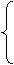
|
|
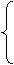 m=
m=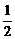 , m=
, m=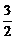 ,
,
n=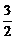 n=
n=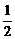 .
.
∴椭圆方程为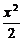 +
+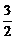 y2=1或
y2=1或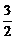 x2+
x2+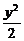 =1.
=1.
6.直线l过点M(1,1),与椭圆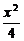 +
+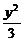 =1相交于A、B两点,若AB的中点为M,试求直线l的方程.
=1相交于A、B两点,若AB的中点为M,试求直线l的方程.
解:设A(x1,y1)、B(x2,y2),
则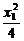 +
+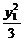 =1, ①
=1, ①
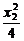 +
+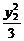 =1. ②
=1. ②
①-②,得
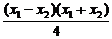 +
+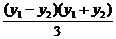 =0.
=0.
∴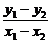 =-
=-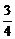 ·
·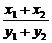 .
.
又∵M为AB中点,
∴x1+x2=2,y1+y2=2.
∴直线l的斜率为-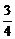 .
.
∴直线l的方程为y-1=-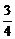 (x-1),
(x-1),
即3x+4y-7=0.
培养能力
5.椭圆对称轴在坐标轴上,短轴的一个端点与两个焦点构成一个正三角形,焦点到椭圆上的点的最短距离是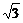 ,求这个椭圆方程.
,求这个椭圆方程.
解:由题设条件可知a=2c,b=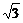 c,又a-c=
c,又a-c=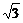 ,解得a2=12,b2=9.∴所求椭圆的方程是
,解得a2=12,b2=9.∴所求椭圆的方程是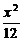 +
+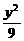 =1或
=1或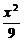 +
+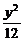 =1.
=1.
4.已知P是椭圆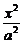 +
+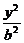 =1(a>b>0)上任意一点,P与两焦点连线互相垂直,且P到两准线距离分别为6、12,则椭圆方程为____________.
=1(a>b>0)上任意一点,P与两焦点连线互相垂直,且P到两准线距离分别为6、12,则椭圆方程为____________.
解析:利用椭圆的两个定义结合勾股定理来求.
答案: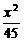 +
+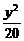 =1
=1
3.(2005年春季北京,10)椭圆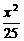 +
+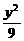 =1的离心率是____________,准线方程是____________.
=1的离心率是____________,准线方程是____________.
解析:由椭圆方程可得a=5,b=3,c=4,e=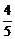 ,准线方程为x=±
,准线方程为x=±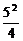 =±
=±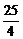 .
.
答案: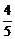 x=±
x=±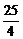
2.(2003年昆明市模拟题)设F1、F2为椭圆的两个焦点,以F2为圆心作圆F2,已知圆F2经过椭圆的中心,且与椭圆相交于M点,若直线MF1恰与圆F2相切,则该椭圆的离心率e为
A. 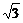 -1
B.2-
-1
B.2-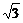 C.
C.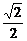 D.
D.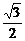
解析:易知圆F2的半径为c,(2a-c)2+c2=4c2,(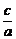 )2+2(
)2+2(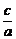 )-2=0,
)-2=0,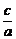 =
=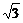 -1.
-1.
答案:A
1.(2004年全国Ⅰ,7)椭圆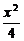 +y2=1的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则|
+y2=1的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则|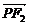 |等于
|等于
A.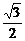 B.
B.
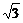 C.
C.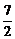 D.4
D.4
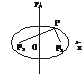
解法一:(如下图)设椭圆的右焦点为F1,左焦点为F2,过F1垂直于x轴的直线与椭圆在第一象限的交点为P.
∵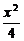 +y2=1,∴a=2,b=1,c=
+y2=1,∴a=2,b=1,c=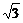 .
.
∴F1(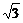 ,0).设P(
,0).设P(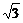 ,yP)代入
,yP)代入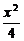 +y2=1,得yP=
+y2=1,得yP=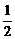 ,
,
∴P(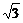 ,
,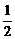 ),|PF1|=
),|PF1|=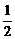 .
.
又∵|PF2|+|PF1|=2a=4,
∴|PF2|=4-|PF1|=4-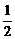 =
=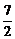 .
.
解法二:椭圆的左准线方程为x=-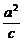 =-
=-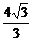 .
.
∵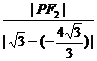 =e=
=e=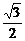 ,∴|PF2|=
,∴|PF2|=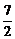 .
.
解法三:由解法一得P(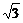 ,
,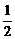 ),
),
又F2(-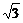 ,0),
,0),
∴|PF2|=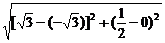 =
=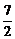 .
.
答案:C
评述:解法一和解法三为基本解法.解法二使用第二定义甚为巧妙.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com