
2.等差数列中,已知五个元素a1,an,n,d,Sn中的任意三个,便可求出其余两个.
1.深刻理解等差数列的定义,紧扣从“第二项起”和“差是同一常数”这两点.
9.有点难度哟!
已知f(x)=a1x+a2x2+a3x3+…+anxn,n为正偶数,且a1,a2,a3,…,an组成等差数列,又f(1)=n2,f(-1)=n.试比较f( )与3的大小.
)与3的大小.
解:∵f(1)=a1+a2+…+an=n2.
依题设,有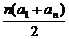 =n2,故a1+an=2n,
=n2,故a1+an=2n,
即2a1+(n-1)d=2n.
又f(-1)=-a1+a2-a3+a4-a5+…-an-1+an=n,
∴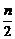 ·d=n,有d=2.进而有2a1+(n-1)2=2n,解出a1=1.
·d=n,有d=2.进而有2a1+(n-1)2=2n,解出a1=1.
于是f(1)=1+3+5+7+…+(2n-1).
f(x)=x+3x2+5x3+7x4+…+(2n-1)xn.
∴f( )=
)= +3(
+3( )2+5(
)2+5( )3+7(
)3+7( )4+…+(2n-1)(
)4+…+(2n-1)( )n. ①
)n. ①
①两边同乘以 ,得
,得
 f(
f( )=(
)=( )2+3(
)2+3( )3+5(
)3+5( )4+…+(2n-3)(
)4+…+(2n-3)( )n+(2n-1)(
)n+(2n-1)( )n+1. ②
)n+1. ②
①-②,得 f(
f( )=
)= +2(
+2( )2+2(
)2+2( )3+…+2(
)3+…+2( )n-(2n-1)(
)n-(2n-1)( )n+1,
)n+1,
即 f(
f( )=
)= +
+ +(
+( )2+…+(
)2+…+( )n-1-(2n-1)(
)n-1-(2n-1)( )n+1.
)n+1.
∴f( )=1+1+
)=1+1+ +
+ +…+
+…+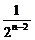 -(2n-1)
-(2n-1)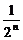 =1+
=1+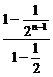 -(2n-1)
-(2n-1)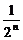 =1+2-
=1+2-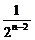 -(2n-1)
-(2n-1)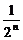 <3.
<3.
∴f( )<3.
)<3.
●思悟小结
8.有点难度哟!
(理)设实数a≠0,函数f(x)=a(x2+1)-(2x+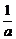 )有最小值-1.
)有最小值-1.
(1)求a的值;
(2)设数列{an}的前n项和Sn=f(n),令bn=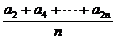 ,证明:数列{bn}是等差数列.
,证明:数列{bn}是等差数列.
(1)解:∵f(x)=a(x-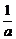 )2+a-
)2+a-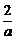 ,由已知知f(
,由已知知f(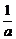 )=a-
)=a-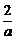 =-1,且a>0,解得a=1,a=-2(舍去).
=-1,且a>0,解得a=1,a=-2(舍去).
(2)证明:由(1)得f(x)=x2-2x,
∴Sn=n2-2n,a1=S1=-1.
当n≥2时,an=Sn-Sn-1=n2-2n-(n-1)2+2(n-1)=2n-3,a1满足上式即an=2n-3.
∵an+1-an=2(n+1)-3-2n+3=2,
∴数列{an}是首项为-1,公差为2的等差数列.
∴a2+a4+…+a2n=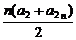
=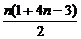 =n(2n-1),
=n(2n-1),
即bn=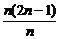 =2n-1.
=2n-1.
∴bn+1-bn=2(n+1)-1-2n+1=2.
又b2=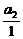 =1,
=1,
∴{bn}是以1为首项,2为公差的等差数列.
(文)有一批影碟机(VCD)原销售价为每台800元,在甲、乙两家电商场均有销售,甲商场用如下的方法促销:买一台单价为780元,买两台单价都为760元,依次类推,每多买一台则所买各台单价均再减少20元,但每台最低价不能低于440元;乙商场一律都按原价的75%销售,某单位需购买一批此类影碟机,问去哪家商场购买花费较少?
解:设单位需购买影碟机n台,在甲商场购买每台售价不低于440元时售价依台数n成等差数列,设该数列为{an},则
an=780+(n-1)×(-20)=800-20n.
由an≥440解不等式800-2n≥440,得n≤18.
当购买台数小于18时,每台售价为800-20n元,在台数大于等于18台时每台售价为440元.
到乙商场购买每台约售价为800×75%=600元.
价差(800-20n)n-600n=20n(10-n).
当n<10时,600n<(800-20n)·n;
当n=10时,600n=(800-20n)·n;
当10<n≤18时,(800-20n)<600n;
当n>18时,440n<600n.
答:当购买少于10台时到乙商场花费较少;当购买10台时到两商场购买花费相同;当购买多于10台时到甲商场购买花费较少.
探究创新
7.已知数列{an}的前n项和为Sn,且满足an+2Sn·Sn-1=0(n≥2),a1= .
.
(1)求证:{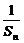 }是等差数列;
}是等差数列;
(2)求an的表达式.
(1)证明:∵-an=2SnSn-1,
∴-Sn+Sn-1=2SnSn-1(n≥2),Sn≠0(n=1,2,3…).
∴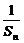 -
-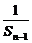 =2.
=2.
又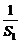 =
=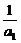 =2,∴{
=2,∴{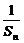 }是以2为首项,2为公差的等差数列.
}是以2为首项,2为公差的等差数列.
(2)解:由(1),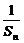 =2+(n-1)·2=2n,∴Sn=
=2+(n-1)·2=2n,∴Sn=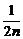 .当n≥2时,an=Sn-Sn-1=
.当n≥2时,an=Sn-Sn-1=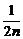 -
-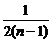 =-
=-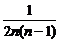 (或n≥2时,an=-2SnSn-1=-
(或n≥2时,an=-2SnSn-1=-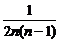 );
);
当n=1时,S1=a1= .
.
∴an=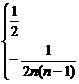
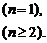
6.设等差数列{an}的前n项和为Sn,已知a3=12,S12>0,S13<0.
(1)求公差d的取值范围;
(2)指出S1,S2,S3,…,S12中哪一个最大,并说明理由.
解:(1)a3=12,∴a1=12-2d,解得a12=12+9d,a13=12+10d.由S12>0,S13<0,即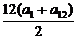 >0,且
>0,且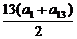 <0,解之得-
<0,解之得-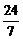 <d<-3.
<d<-3.
(2)由an=12+(n-3)d>0,由-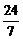 <d<-3,易知a7<0,a6>0,故S6最大.
<d<-3,易知a7<0,a6>0,故S6最大.
培养能力
5.(2004年全国,文17)等差数列{an}的前n项和为Sn,已知a10=30,a20=50.
(1)求通项{an};
(2)若Sn=242,求n.
解:(1)由an=a1+(n-1)d,a10=30,a20=50,
得方程组a1+9d=30, ①
a1+19d=50. ②
由①②解得a1=12,d=2,故an=2n+10.
(2)由Sn=na1+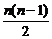 d及Sn=242,得方程12n+
d及Sn=242,得方程12n+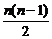 ×2=242,解得n=11或n=-22(舍).
×2=242,解得n=11或n=-22(舍).
4.将正偶数按下表排成5列:
|
|
第1列 |
第2列 |
第3列 |
第4列 |
第5列 |
|
第1行 |
|
2 |
4 |
6 |
8 |
|
第2行 |
16 |
14 |
12 |
10 |
|
|
第3行 |
|
18 |
20 |
22 |
24 |
|
…… |
|
…… |
28 |
26 |
|
那么2004应该在第______________行第______________列.
解法一:由2004是正偶数列中第1002项,每一行四项,故在第251行中的第二个数.又第251行是从左向右排且从第二行开始排,故2004为第251行第3列.
解法二:观察第三列中的各数,可发现从上依次组成一个首项为4,公差为8的等差数列,可算得2004为此数列的第251项.
答案:251 3
3.在等差数列{an}中,公差为 ,且a1+a3+a5+…+a99=60,则a2+a4+a6+…+a100=_________.
,且a1+a3+a5+…+a99=60,则a2+a4+a6+…+a100=_________.
解析:由等差数列的定义知a2+a4+a6+…+a100=a1+a3+a5+…+a99+50d=60+25=85.
答案:85
2.等差数列{an}的前n项和记为Sn,若a2+a4+a15的值是一个确定的常数,则数列{Sn}中也为常数的项是
A.S7 B.S8 C.S13 D.S15
解析:设a2+a4+a15=p(常数),
∴3a1+18d=p,即a7=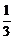 p.
p.
∴S13=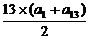 =13a7=
=13a7=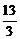 p.
p.
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com