
7.(2002年春季北京,21)已知点的序列An(xn,0),n∈N*,其中xl=0,x2=a(a>0),A3是线段AlA2的中点,A4是线段A2A3的中点,…,An是线段An-2An-1的中点,….
(1)写出xn与xn-1、xn-2之间的关系式(n≥3);
(2)设an=xn+1-xn,计算al,a2,a3,由此推测数列{an}的通项公式,并加以证明.
解:(1)当n≥3时,xn=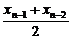 .
.
(2)a1=x2-x1=a,a2=x3-x2=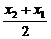 -x2=-
-x2=-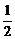 (x2-x1)=-
(x2-x1)=-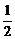 a,
a,
a3=x4-x3=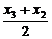 -x3=-
-x3=-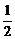 (x3-x2)=-
(x3-x2)=-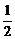 (-
(-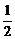 a)=
a)=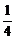 a,
a,
由此推测:an=(-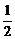 )n-1a(n∈N*).
)n-1a(n∈N*).
证明如下:因为a1=a>0,且an=xn+1-xn=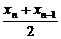 -xn=
-xn=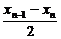 =-
=-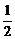 (xn-xn-1)=-
(xn-xn-1)=-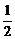 an-1(n≥2),所以an=(-
an-1(n≥2),所以an=(-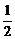 )n-1a.
)n-1a.
探究创新
(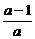 )8+(
)8+(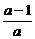 )9=(
)9=(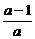 )8(1+
)8(1+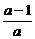 )
)
=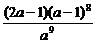 .
.
培养能力
6.已知直线l上有一列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,其中n∈N*,x1=1,x2=2,点Pn+2分有向线段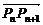 所成的比为λ(λ≠-1).
所成的比为λ(λ≠-1).
(1)写出xn+2与xn+1,xn之间的关系式;
(2)设an=xn+1-xn,求数列{an}的通项公式.
解:(1)由定比分点坐标公式得xn+2=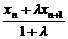 .
.
(2)a1=x2-x1=1,
an+1=xn+2-xn+1=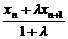 -xn+1
-xn+1
=-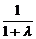 (xn+1-xn)=-
(xn+1-xn)=-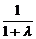 an,
an,
∴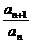 =-
=-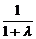 ,即{an}是以a1=1为首项,-
,即{an}是以a1=1为首项,-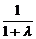 为公比的等比数列.
为公比的等比数列.
∴an=(-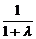 )n-1.
)n-1.
3.用函数的观点和方法揭示等差数列和等比数列的特征,在分析和解决有关数列的综合题中具有重要的意义.
拓展题例
[例题] 已知数列{an},构造一个新数列a1,(a2-a1),(a3-a2),…,(an-an-1),…,此数列是首项为1,公比为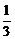 的等比数列.
的等比数列.
(1)求数列{an}的通项;
(2)求数列{an}的前n项和Sn.
解:(1)由题意an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=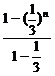 =
=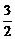 [1-(
[1-(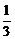 )n].
)n].
(2)Sn=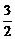 [n-(
[n-(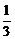 +
+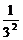 +
+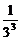 +…+
+…+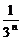 )]=
)]=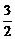 [n-
[n- (1-
(1-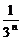 )]=
)]=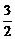 n-
n-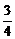 +
+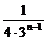 .
.
2.从等差数列中按某种规律,抽取某些项,依次排列,组成一个等比数列,是等差、等比数列综合题中的较重要的类型,要认真体会此类题.
1.等差、等比数列是两种最基本、最常见的数列,灵活地运用等差、等比数列的性质,能使问题简化;灵活地运用通项公式和前n项和公式解题是高考考查的重点.
8.有点难度哟!
(理)已知数列{an}的各项均为正整数,且满足an+1=an2-2nan+2(n∈N*),又a5=11.
(1)求a1,a2,a3,a4的值,并由此推测出{an}的通项公式(不要求证明);
(2)设bn=11-an,Sn=b1+b2+…+bn,Sn′=|b1|+|b2|+…+|bn|,求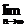
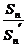 的值.
的值.
解:(1)由a5=11,得11=a42-8a4+2,即a42-8a4-9=0.解得a4=9或a4=-1(舍).
由a4=9,得a32-6a3-7=0.
解得a3=7或a3=-1(舍).
同理可求出a2=5,a1=3.
由此推测an的一个通项公式an=2n+1(n∈N*).
(2)bn=11-an=10-2n(n∈N*),可知数列{bn}是等差数列.
Sn=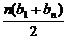 =
=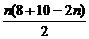 =-n2+9n.
=-n2+9n.
当n≤5时,Sn′=Sn=-n2+9n;
当n>5时,Sn′=-Sn+2S5=-Sn+40=n2-9n+40.
当n≤5时,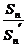 =1;
=1;
当n>5时,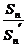 =
=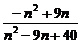 .
.
∴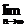
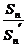 =
=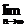
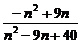 =-1.
=-1.
(文)设f(k)是满足不等式log2x+log2(3·2k-1-x)≥2k-1(k∈N*)的自然数x的个数.
(1)求f(k)的表达式;
(2)记Sn=f(1)+f(2)+…+f(n),Pn=n2+n-1,当n≤5时试比较Sn与Pn的大小.
解:(1)由不等式log2x+log2(3·2k-1-x)≥2k-1,得x(3·2k-1-x)≥22k-1,解之得2k-1≤x≤2k,故f(k)=2k-2k-1+1=2k-1+1.
(2)∵Sn=f(1)+f(2)+…+f(n)=1+2+22+23+…+2n-1+n=2n+n-1,
∴Sn-Pn=2n+n-1-(n2+n-1)=2n-n2.
又n≤5,可计算得S1>P1,S2=P2,S3<P3,S4=P4,S5>P5.
●思悟小结
本节加强了数列知识与函数、不等式、方程、对数、立体几何、三角等内容的综合.解决这些问题要注意:
(1)通过知识间的相互转化,使学生更好地掌握数学中的转化思想.
(2)通过解数列与其他知识的综合问题,培养学生分析问题和解决问题的综合能力.
●教师下载中心
教学点睛
本节教学中应注意以下几个问题:
7.数列{an}中,a1=8,a4=2,且满足an+2-2an+1+an=0(n∈N*).
(1)求数列{an}的通项公式.
(2)设bn=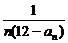 (n∈N*),Sn=b1+b2+…+bn,是否存在最大的整数m,使得任意的n均有Sn>
(n∈N*),Sn=b1+b2+…+bn,是否存在最大的整数m,使得任意的n均有Sn> 总成立?若存在,求出m;若不存在,请说明理由.
总成立?若存在,求出m;若不存在,请说明理由.
解:(1)∵an+2-2an+1+an=0,
∴an+2-an+1=an+1-an(n∈N*).
∴{an}是等差数列.设公差为d,
又a1=8,a4=a1+3d=8+3d=2,
∴d=-2.∴an=-2n+10.
(2)bn=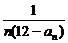 =
=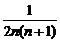
= (
(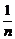 -
-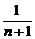 ),
),
∴Sn=b1+b2+…+bn= [(1-
[(1- )+(
)+( -
-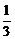 )+…+(
)+…+(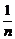 -
-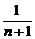 )]
)]
= (1-
(1-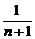 )=
)=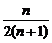 .
.
假设存在整数m满足Sn> 总成立.
总成立.
又Sn+1-Sn=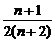 -
-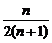
=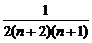 >0,
>0,
∴数列{Sn}是单调递增的.
∴S1=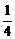 为Sn的最小值,故
为Sn的最小值,故 <
<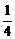 ,
,
即m<8.又m∈N*,
∴适合条件的m的最大值为7.
探究创新
6.(2003年北京高考,文16)已知数列{an}是等差数列,且a1=2,a1+a2+a3=12.
(1)求数列{an}的通项公式;
(2)令bn=anxn(x∈R),求数列{bn}前n项和的公式.
解:(1)设数列{an}的公差为d,
则a1+a2+a3=3a1+3d=12.
又a1=2,得d=2.
所以an=2n.
(2)令Sn=b1+b2+…+bn,
则由bn=anxn=2nxn,得
Sn=2x+4x2+…+(2n-2)xn-1+2nxn, ①
xSn=2x2+4x3+…+(2n-2)xn+2nxn+1. ②
当x≠1时,①式减去②式,得
(1-x)Sn=2(x+x2+…+xn)-2nxn+1
=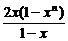 -2nxn+1.
-2nxn+1.
所以Sn=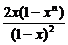 -
-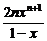 .
.
当x=1时,Sn=2+4+…+2n=n(n+1).
综上可得,当x=1时,Sn=n(n+1);
当x≠1时,Sn=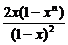 -
-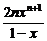 .
.
5.设{an}为等比数列,a1=b1=1,a2+a4=b3,b2b4=a3,分别求出{an}及{bn}的前10项的和S10及T10.
解:设公差为d,公比为q,由题意知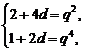
∴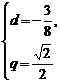 或
或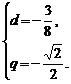
∴S10=10+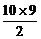 (-
(-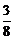 )=-
)=-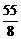 .
.
当q=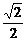 时,T10=
时,T10=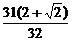 ;
;
当q=-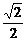 时,T10=
时,T10=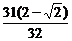 .
.
培养能力
4.已知数列{an}中,a1=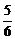 且对任意非零自然数n都有an+1=
且对任意非零自然数n都有an+1=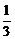 an+(
an+( )n+1.数列{bn}对任意非零自然数n都有bn=an+1-
)n+1.数列{bn}对任意非零自然数n都有bn=an+1- an.
an.
(1)求证:数列{bn}是等比数列;
(2)求数列{an}的通项公式.
(1)证明:bn=an+1- an=[
an=[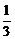 an+(
an+( )n+1]-
)n+1]- an=(
an=( )n+1-
)n+1-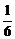 an,bn+1=(
an,bn+1=( )n+2-
)n+2-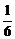 an+1=(
an+1=( )n+2-
)n+2-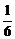 [
[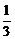 an+(
an+( )n+1]=
)n+1]= ·(
·( )n+1-
)n+1-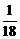 an-
an-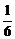 ·(
·( )n+1=
)n+1=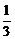 ·(
·( )n+1-
)n+1-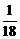 an=
an=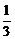 ·[(
·[( )n+1-
)n+1-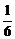 an],
an],
∴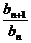 =
=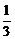 (n=1,2,3,…).
(n=1,2,3,…).
∴{bn}是公比为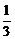 的等比数列.
的等比数列.
(2)解:∵b1=( )2-
)2-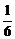 a1=
a1=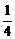 -
-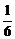 ·
·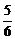 =
=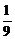 ,∴bn=
,∴bn=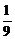 ·(
·(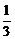 )n-1=(
)n-1=(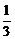 )n+1.由bn=(
)n+1.由bn=( )n+1-
)n+1-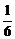 an,得(
an,得(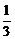 )n+1=(
)n+1=( )n+1-
)n+1-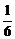 an,解得an=6[(
an,解得an=6[( )n+1-(
)n+1-(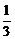 )n+1].
)n+1].
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com