
3.解题中,应重视双曲线两种定义的灵活应用,以减少运算量.
●教师下载中心
教学点睛
本节的重点是双曲线的定义、方程、几何性质.难点是理解参数a、b、c、e的关系及渐近线方程、准线方程、第二定义的应用.关键是准确理解和掌握有关概念,灵活地运用数形结合、函数与方程的思想及等价转化的思想.为此建议在教学中注意以下几点:
2.由已知双曲线的方程求基本量,注意首先应将方程化为标准形式,再计算,并要特别注意焦点位置,防止将焦点坐标和准线方程写错.
1.由给定条件求双曲线的方程,常用待定系数法.首先是根据焦点位置设出方程的形式(含有参数),再由题设条件确定参数值,应特别注意:
(1)当焦点位置不确定时,方程可能有两种形式,应防止遗漏;
(2)已知渐近线的方程bx±ay=0,求双曲线方程,可设双曲线方程为b2x2-a2y2=λ(λ≠0),根据其他条件确定λ的值.若求得λ>0,则焦点在x轴上,若求得λ<0,则焦点在y轴上.
9.(2003年春季上海)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线C′: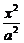 -
-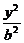 =1写出具有类似特性的性质,并加以证明.
=1写出具有类似特性的性质,并加以证明.
解:类似的性质为若MN是双曲线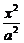 -
-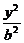 =1上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.
=1上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.
设点M的坐标为(m,n),
则点N的坐标为(-m,-n),
其中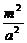 -
-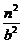 =1.
=1.
又设点P的坐标为(x,y),
由kPM= ,kPN=
,kPN= ,
,
得kPM·kPN= ·
· =
=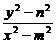 ,
,
将y2=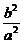 x2-b2,n2=
x2-b2,n2=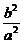 m2-b2,代入得
m2-b2,代入得
kPM·kPN=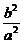 .
.
评注:本题主要考查椭圆、双曲线的基本性质,考查类比、归纳、探索问题的能力.它是一道综合椭圆和双曲线基本知识的综合性题目,对思维能力有较高的要求.
●思悟小结
本节重点是求双曲线方程及由双曲线方程求基本量,难点是双曲线的灵活运用.解决本节问题应注意以下几点:
8.(理)已知l1、l2是过点P(-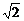 ,0)的两条互相垂直的直线,且l1、l2与双曲线
y2-x2=1各有两个交点,分别为A1、B1和A2、B2.
,0)的两条互相垂直的直线,且l1、l2与双曲线
y2-x2=1各有两个交点,分别为A1、B1和A2、B2.
(1)求l1的斜率k1的取值范围;
(2)若|A1B1|=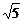 |A2B2|,求l1、l2的方程.
|A2B2|,求l1、l2的方程.
解:(1)显然l1、l2斜率都存在,否则l1、l2与曲线不相交.设l1的斜率为k1,则l1的方程为y=k1(x+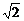 ).
).
|
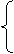 y=k1(x+
y=k1(x+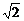 ),
),
y2-x2=1,消去y得
(k12-1)x2+2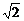 k12x+2k12-1=0. ①
k12x+2k12-1=0. ①
根据题意得k12-1≠0, ②
Δ1>0,即有12k12-4>0. ③
完全类似地有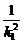 -1≠0, ④
-1≠0, ④
Δ2>0,即有12·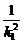 -4>0, ⑤
-4>0, ⑤
从而k1∈(-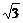 ,-
,-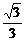 )∪(
)∪(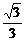 ,
,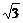 )且k1≠±1.
)且k1≠±1.
(2)由弦长公式得
|A1B1|=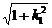
 . ⑥
. ⑥
完全类似地有
|A2B2|=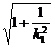
 . ⑦
. ⑦
∵|A1B1|=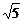 |A2B2|,
|A2B2|,
∴k1=±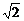 ,k2=
,k2=
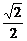 .从而
.从而
l1:y=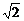 (x+
(x+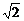 ),l2:y=-
),l2:y=-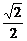 (x+
(x+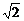 )或l1:y=-
)或l1:y=-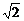 (x+
(x+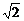 ),l2:y=
),l2:y=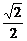 (x+
(x+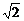 ).
).
(文)在双曲线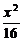 -
-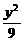 =1上求一点M,使它到左右两焦点的距离之比为3∶2,并求M点到两准线的距离.
=1上求一点M,使它到左右两焦点的距离之比为3∶2,并求M点到两准线的距离.
解:设M(x1,y1),左右两焦点F1、F2,由双曲线第二定义得
|MF1|=ex1+a,|MF2|=ex1-a,
由已知2(ex1+a)=3(ex1-a),
把e=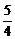 ,a=4代入,得x1=16,y1=±3
,a=4代入,得x1=16,y1=±3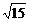 .
.
∴点M的坐标为(16,±3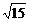 ).
).
双曲线准线方程为x=±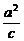 =±
=± .
.
∴M(16,±3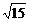 )到准线的距离为12
)到准线的距离为12 或19
或19 .
.
探究创新
7.双曲线kx2-y2=1,右焦点为F,斜率大于0的渐近线为l,l与右准线交于A,FA与左准线交于B,与双曲线左支交于C,若B为AC的中点,求双曲线方程.
解:由题意k>0,c= ,
,
渐近线方程l为y= x,
x,
准线方程为x=± ,于是A(
,于是A( ,
,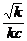 ),
),
直线FA的方程为 y=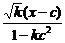 ,
,
于是B(- ,
,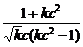 ).
).
由B是AC中点,则xC=2xB-xA=- ,
,
yC=2yB-yA=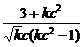 .
.
将xC、yC代入方程kx2-y2=1,得
k2c4-10kc2+25=0.
解得k(1+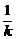 )=5,则k=4.
)=5,则k=4.
所以双曲线方程为4x2-y2=1.
6.已知双曲线x2-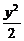 =1与点P(1,2),过P点作直线l与双曲线交于A、B两点,若P为AB中点.
=1与点P(1,2),过P点作直线l与双曲线交于A、B两点,若P为AB中点.
(1)求直线AB的方程;
(2)若Q(1,1),证明不存在以Q为中点的弦.
(1)解:设过P(1,2)点的直线AB方程为y-2=k(x-1),
代入双曲线方程得
(2-k2)x2+(2k2-4k)x-(k4-4k+6)=0.
设A(x1,y1),B(x2,y2),
则有x1+x2=-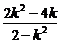 ,
,
由已知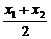 =xp=1,
=xp=1,
∴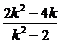 =2.解得k=1.
=2.解得k=1.
又k=1时,Δ=16>0,从而直线AB方程为x-y+1=0.
(2)证明:按同样方法求得k=2,而当k=2时,Δ<0,所以这样的直线不存在.
培养能力
5.已知双曲线的方程是16x2-9y2=144.
(1)求这双曲线的焦点坐标、离心率和渐近线方程;
(2)设F1和F2是双曲线的左、右焦点,点P在双曲线上,且|PF1|·|PF2|=32,求∠F1PF2的大小.
解:(1)由16x2-9y2=144得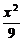 -
-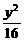 =1,
=1,
∴a=3,b=4,c=5.焦点坐标F1(-5,0),F2(5,0),离心率e=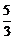 ,渐近线方程为y=±
,渐近线方程为y=±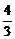 x.
x.
(2)||PF1|-|PF2||=6,cos∠F1PF2=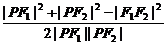
=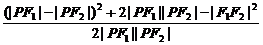 =
= =0.
=0.
∴∠F1PF2=90°.
4.过点A(0,2)可以作____________条直线与双曲线x2-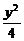 =1有且只有一个公共点.
=1有且只有一个公共点.
解析:数形结合,两切线、两交线.
答案:4
3.(2003年上海)给出问题:F1、F2是双曲线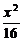 -
-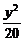 =1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点F2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
=1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点F2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
该学生的解答是否正确?若正确,请将他的解题依据填在下面横线上;若不正确,将正确结果填在下面横线上.
______________________________________________________.
解析:易知P与F1在y轴的同侧,|PF2|-|PF1|=2a,∴|PF2|=17.
答案:|PF2|=17
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com