2.余弦二倍角公式有多种形式即cos2α=cos²α－sin²α=2cos²α－1=1－2sin²α.变形公式sin²α=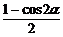，cos²α=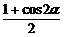.它的双向应用分别起到缩角升幂和扩角降幂作用.

●点击双基

1.在公式S_(α+β)、C_(α+β)、T_(α+β)中，当α=β时，就可得到公式S_2α、C_2α、T_2α，在公式S_2α、C_2α中角α没有限制在T_2α中，只有当α≠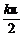+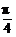且α≠kπ+时，公式才成立.

4.3　 两角和与差、二倍角的公式(二)

●知识梳理

2.公式应用讲究一个“活”字，即正用、逆用、变形用，还要创造条件应用公式.如拆角、拼角技巧等，要注意结合题目使学生体会其间的规律.

拓展题例

[例1] 已知a=(cosα，sinα)，b=(cosβ，sinβ)，(a≠b).

求证：(a+b)⊥(a－b).

分析：只要证(a+b)·(a－b)=0即可.

证法一：(a+b)·(a－b)=|a|²－|b|²=1－1=0，∴(a+b)⊥(a－b).

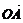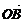证法二：在单位圆中设=a，=b，以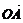、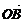为邻边作□OACB，则OACB为菱形.

∴⊥.

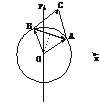
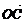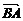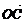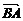∴·=0，

即(a+b)·(a－b)=0.

∴(a+b)⊥(a－b).

[例2] α、β∈(0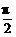，)，3sin²α+2sin²β=1，①　 3sin2α－2sin2β=0②，求α+2β的值.

解：由①得3sin²α=1－2sin²β=cos2β.

由②得sin2β=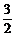sin2α.

∴cos(α+2β)=cosαcos2β－sinαsin2β

=3cosαsin²α－sinα·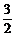sin2α=0.

∵α、β∈(0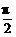，)，∴α+2β∈(0，).

∴α+2β=.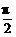

1.本节公式多，内在联系密切，建议复习时，要使学生理清公式间的推导线索，让学生亲自推导一下C_(α+β).

4.要时时注意角的范围的讨论.

●教师下载中心

教学点睛

3.注意倍角的相对性，如3α是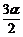的倍角.

2.注意拆角、拼角技巧，如α=(α+β)－β，2α=(α+β)+(α－β)等.

1.不仅要能熟练推证公式(建议自己推证一遍所有公式)、熟悉公式的正用逆用，还要熟练掌握公式的变形应用.

10.sinα+sinβ=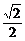，求cosα+cosβ的取值范围.

解：令t=cosα+cosβ，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

sinα+sinβ=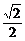，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

①²+②²，得t²+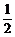=2+2cos(α－β).

∴2cos(α－β)=t²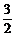－∈［－2，2］.

∴t∈［－，］.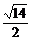

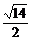●思悟小结