
9.已知平面向量a=(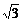 ,-1),b=(
,-1),b=(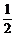 ,
,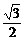 ),
),
(1)证明:a⊥b;
(2)若存在不同时为零的实数k和t,使x=a+(t2-3)b,y=-ka+tb,且x⊥y,试求函数关系式k=f(t);
(3)据(2)的结论,确定函数k=f(t)的单调区间.
(1)证明:a·b=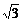 ×
×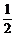 +(-1)×
+(-1)×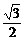 =0.
=0.
(2)解:∵x⊥y,∴x·y=0,且a·b=0,a2=4,b2=1,整理得-4k+t(t2-3)=0,
∴k=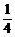 t(t2-3).
t(t2-3).
(3)解:记f(t)=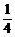 (t3-3t),∴
(t3-3t),∴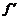 (t)=
(t)=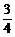 t2-
t2-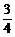 .令
.令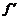 (t)>0得t<-1或t>1.因此,当t∈(-∞,-1)时,f(t)是增函数;当t∈(1,+∞)时,f(t)也是增函数.再令
(t)>0得t<-1或t>1.因此,当t∈(-∞,-1)时,f(t)是增函数;当t∈(1,+∞)时,f(t)也是增函数.再令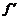 (t)<0,得-1<t<1,故t∈(-1,1)时,f(t)是减函数.
(t)<0,得-1<t<1,故t∈(-1,1)时,f(t)是减函数.
●思悟小结
8.已知F1(-1,0),F2(1,0),A(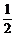 ,0),动点P满足3
,0),动点P满足3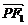 ·
·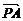 +
+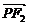 ·
·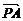 =0.
=0.
(1)求动点P的轨迹方程.
(2)是否存在点P,使PA成为∠F1PF2的平分线?若存在,求出P点坐标;若不存在,请说明理由.
解:(1)设P(x,y),则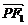 =(-1-x,-y),
=(-1-x,-y),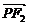 =(1-x,-y),
=(1-x,-y),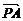 =(
=(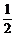 -x,-y).
-x,-y).
∴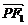 ·
·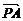 =(-1-x)(
=(-1-x)(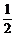 -x)+(-y)2=(x+1)(x-
-x)+(-y)2=(x+1)(x-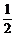 )2+y2,
)2+y2,
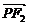 ·
·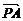 =(1-x)·(
=(1-x)·(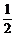 -x)+(-y)2=(x-1)(x-
-x)+(-y)2=(x-1)(x-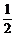 )+y2.
)+y2.
∴3[(x+1)(x-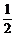 )+y2]+(x-1)(x-
)+y2]+(x-1)(x-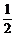 )+y2=0.
)+y2=0.
∴x2+y2=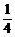 即为P点的轨迹方程.
即为P点的轨迹方程.
(2)设存在,则cos∠F1PA=cos∠APF2.
∴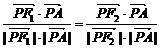 .
.
将条件3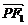 ·
·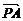 =-
=-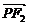 ·
·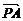 代入上式不成立.∴不存在.
代入上式不成立.∴不存在.
探究创新
7.(2004年浙江,14)(理)已知平面上三点A、B、C满足| |=3,|
|=3,|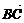 |=4,|
|=4,|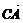 |=5,则
|=5,则 ·
·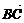 +
+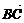 ·
·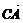 +
+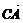 ·
· 的值等于_______.
的值等于_______.
解析:∵| |2+|
|2+|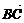 |2=|
|2=|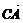 |2,
|2,
∴△ABC为直角三角形,其中∠B=90°.
∴ ·
·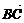 +
+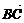 ·
·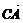 +
+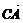 ·
· =0+|
=0+|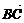 ||
||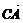 |cos(π-∠C)+|
|cos(π-∠C)+|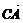 ||
|| |cos(π-∠A)=-25.
|cos(π-∠A)=-25.
答案:-25
(文)已知平面上三点A、B、C满足| |=2,|
|=2,|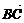 |=1,|
|=1,|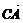 |=
|=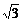 ,则
,则 ·
·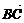 +
+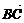 ·
·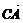 +
+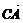 ·
· 的值等于_________.
的值等于_________.
解析:∵|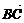 |2+|
|2+|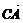 |2=|
|2=| |2,
|2,
∴△ABC为直角三角形且∠C=90°.
∴ ·
·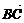 +
+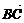 ·
·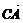 +
+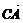 ·
· =|
=| ||
||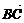 |cos(π-∠B)+0+|
|cos(π-∠B)+0+|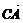 ||
|| |cos(π-∠A)=-4.
|cos(π-∠A)=-4.
答案:-4
6.如下图,以原点和A(5,2)为两个顶点作等腰直角△OAB,使∠B=90°.
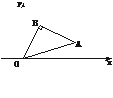
求点B和向量 的坐标.
的坐标.
分析:这里关键是求出B点的坐标,设B(x,y),由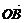 ⊥
⊥ 和|
和|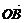 |=|
|=| |,则可列出x、y的方程组.
|,则可列出x、y的方程组.
解:设B点坐标为(x,y),
则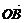 =(x,y),
=(x,y), =(x-5,y-2).
=(x-5,y-2).
∵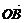 ⊥
⊥ ,∴x(x-5)+y(y-2)=0,
,∴x(x-5)+y(y-2)=0,
即x2+y2-5x-2y=0. ①
又|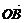 |=|
|=| |,
|,
∴x2+y2=(x-5)2+(y-2)2,
即10x+4y=29. ②
解①②得
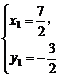 或
或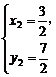
∴B点坐标为(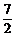 ,-
,-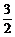 )或(
)或(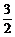 ,
,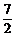 ).
).
故 =(-
=(-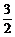 ,-
,-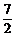 )或
)或 =(-
=(-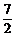 ,
,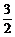 )
)
培养能力
5.已知|a|=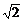 ,|b|=3,a和b的夹角为45°,求当向量a+λb与λa+b的夹角为锐角时,λ的取值范围.
,|b|=3,a和b的夹角为45°,求当向量a+λb与λa+b的夹角为锐角时,λ的取值范围.
解:a+λb与λa+b的夹角为锐角,
即(a+λb)·(λa+b)>0,
也就是λa2+(λ2+1)a·b+λb2>0,
即2λ+(λ2+1)·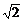 ·3·
·3·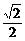 +9λ>0,
+9λ>0,
解得λ<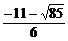 或λ>
或λ>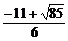 .
.
4.给出下列命题:
①若a2+b2=0,则a=b=0;
②已知a、b、c是三个非零向量,若a+b=0,
则|a·c|=|b·c|;
③在△ABC中,a=5,b=8,c=7,则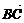 ·
·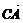 =20;
=20;
④a与b是共线向量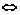 a·b=|a||b|.
a·b=|a||b|.
其中真命题的序号是_______.(请把你认为是真命题的序号都填上)
解析:①a2+b2=0,∴|a|=-|b|.
又|a|≥0,|b|≥0,
∴|a|=|b|=0.∴a=b=0.∴①正确.
②a+b=0,∴a=-b,|a·c|=|a||c||cos〈a,c〉|,|b·c|=|b||c||cos〈b,c〉|=|a||c||cos〈-a,c〉|=
|a||c||cos(π-〈a,c〉)|=|a||c||cos〈a,c〉|.∴②正确.
③cosC=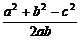 =
=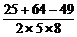 =
=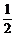 .
.
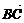 ·
·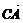 =|
=|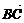 ||
||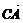 |cos(π-C)=5×8×(-
|cos(π-C)=5×8×(-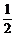 )=-20.∴③不正确.
)=-20.∴③不正确.
④a与b是共线向量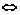 a=λb(b≠0)
a=λb(b≠0)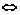 a·b=λb2,而|a||b|=|λb||b|=|λ||b|2.
a·b=λb2,而|a||b|=|λb||b|=|λ||b|2.
∴④不正确.
答案:①②
3.若向量c垂直于向量a和b,d=λa+μb(λ、μ∈R,且λμ≠0),则
A.c∥d
B.c⊥d
C.c不平行于d,也不垂直于d
D.以上三种情况均有可能
解析:∵c⊥a,c⊥b,∴c·a=0,c·b=0.
∴c·d=c·(λa+μb)=c·(λa)+c·(μb)=λc·a+μc·b=0.
答案:B
2.已知|a|=10,|b|=12,且(3a)·(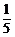 b)=-36,则a与b的夹角是
b)=-36,则a与b的夹角是
A.60° B.120° C.135° D.150°
解析:由(3a)·(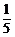 b)=-36得a·b=-60.
b)=-36得a·b=-60.
∴cos〈a,b〉=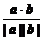
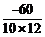 =-
=-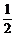 .
.
又0°≤〈a,b〉≤180°,∴〈a,b〉=120°.
答案:B
1.若a=(2,3),b=(-4,7),则a在b方向上的投影为
A.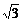 B.
B.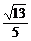 C.
C.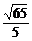 D.
D.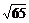
解析:a在b方向上的投影为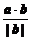 =
=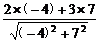 =
=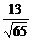 =
=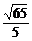 .
.
答案:C
4.(2004年上海,6)(理)已知点A(1,-2),若向量 与a=(2,3)同向,|
与a=(2,3)同向,| |=2
|=2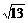 ,则点B的坐标为____________.
,则点B的坐标为____________.
解析:设A点坐标为(xA,yA),B点坐标为(xB,yB).
∵ 与a同向,∴可设
与a同向,∴可设 =λa=(2λ,3λ)(λ>0).
=λa=(2λ,3λ)(λ>0).
∴| |=
|=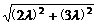 =2
=2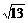 ,∴λ=2.
,∴λ=2.
则 =(xB-xA,yB-yA)=(4,6),
=(xB-xA,yB-yA)=(4,6),
∴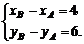 ∵
∵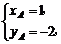 ∴
∴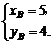
∴B点坐标为(5,4).
答案:(5,4)
(文)已知点A(-1,-5)和向量a=(2,3),若 =3a,则点B的坐标为____________.
=3a,则点B的坐标为____________.
解析:设B点坐标为(xB,yB),
则 =(xB+1,yB+5)=3a=(6,9),
=(xB+1,yB+5)=3a=(6,9),
∴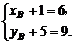 ∴
∴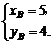
∴B(5,4).
答案:(5,4)
●典例剖析
[例1] 判断下列各命题正确与否:
(1)若a≠0,a·b=a·c,则b=c;
(2)若a·b=a·c,则b≠c当且仅当a=0时成立;
(3)(a·b)c=a(b·c)对任意向量a、b、c都成立;
(4)对任一向量a,有a2=|a|2.
剖析:(1)(2)可由数量积的定义判断.(3)通过计算判断.(4)把a2转化成a·a=|a|2可判断.
解:(1)a·b=a·c,∴|a||b|cosα=|a||c|cosβ(其中α、β分别为a与b,a与c的夹角).∵|a|≠0,∴|b|cosα=|c|cosβ.
∵cosα与cosβ不一定相等,∴|b|与|c|不一定相等.∴b与c也不一定相等.∴(1)不正确.
(2)若a·b=a·c,则|a||b|cosα=|a||c|cosβ(α、β为a与b,a与c的夹角).
∴|a|(|b|cosα-|c|cosβ)=0.
∴|a|=0或|b|cosα=|c|cosβ.
当b≠c时,|b|cosα与|c|cosβ可能相等.
∴(2)不正确.
(3)(a·b)c=(|a||b|cosα)c,
a(b·c)=a|b||c|cosθ(其中α、θ分别为a与b,b与c的夹角).
(a·b)c是与c共线的向量,
a(b·c)是与a共线的向量.
∴(3)不正确.(4)正确.
评述:判断上述问题的关键是要掌握向量的数量积的含义,向量的数量积的运算律不同于实数乘法的运算律.
[例2] 平面内有向量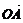 =(1,7),
=(1,7),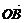 =(5,1),
=(5,1),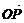 =(2,1),点X为直线OP上的一个动点.
=(2,1),点X为直线OP上的一个动点.
(1)当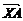 ·
·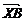 取最小值时,求
取最小值时,求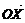 的坐标;
的坐标;
(2)当点X满足(1)的条件和结论时,求cos∠AXB的值.
剖析:因为点X在直线OP上,向量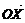 与
与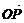 共线,可以得到关于
共线,可以得到关于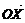 坐标的一个关系式,再根据
坐标的一个关系式,再根据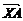 ·
·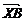 的最小值,求得
的最小值,求得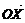 的坐标,而cos∠AXB是
的坐标,而cos∠AXB是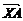 与
与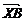 夹角的余弦,利用数量积的知识易解决.
夹角的余弦,利用数量积的知识易解决.
解:(1)设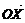 =(x,y),
=(x,y),
∵点X在直线OP上,∴向量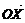 与
与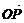 共线.
共线.
又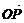 =(2,1),∴x-2y=0,即x=2y.
=(2,1),∴x-2y=0,即x=2y.
∴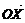 =(2y,y).又
=(2y,y).又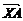 =
=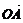 -
-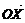 ,
,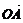 =(1,7),
=(1,7),
∴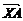 =(1-2y,7-y).
=(1-2y,7-y).
同样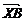 =
=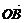 -
-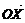 =(5-2y,1-y).
=(5-2y,1-y).
于是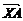 ·
·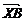 =(1-2y)(5-2y)+(7-y)(1-y)=5y2-20y+12=5(y-2)2-8.
=(1-2y)(5-2y)+(7-y)(1-y)=5y2-20y+12=5(y-2)2-8.
∴当y=2时,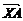 ·
·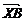 有最小值-8,此时
有最小值-8,此时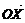 =(4,2).
=(4,2).
(2)当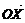 =(4,2),即y=2时,有
=(4,2),即y=2时,有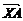 =(-3,5),
=(-3,5),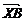 =(1,-1).
=(1,-1).
∴|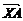 |=
|=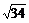 ,|
,|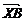 |=
|=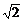 .
.
∴cos∠AXB=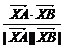 =-
=-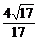 .
.
评述:(1)中最值问题不少都转化为函数最值问题解决,因此解题关键在于寻找变量,以构造函数.而(2)中即为数量积定义的应用.
[例3] 已知向量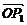 、
、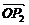 、
、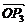 满足
满足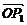 +
+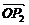 +
+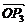 =0,|
=0,|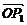 |=|
|=|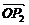 |=|
|=|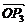 |=1.
|=1.
求证:△P1P2P3是正三角形.
剖析:由|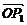 |=|
|=|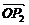 |=|
|=|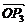 |=1知O是△P1P2P3的外接圆的圆心,要证△P1P2P3是正三角形,只需证∠P1OP2=∠P2OP3=∠P3OP1即可,即需求
|=1知O是△P1P2P3的外接圆的圆心,要证△P1P2P3是正三角形,只需证∠P1OP2=∠P2OP3=∠P3OP1即可,即需求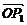 与
与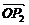 ,
,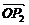 与
与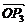 ,
,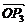 与
与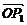 的夹角.由
的夹角.由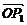 +
+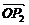 +
+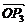 =0变形可出现数量积,进而求夹角.
=0变形可出现数量积,进而求夹角.
证明:∵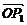 +
+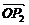 +
+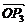 =0,∴
=0,∴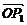 +
+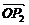 =-
=-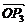 .∴|
.∴|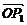 +
+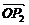 |=|-
|=|-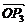 |.
|.
∴|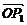 |2+|
|2+|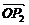 |2+2
|2+2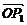 ·
·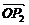 =|
=|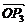 |2.
|2.
又∵|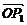 |=|
|=|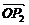 |=|
|=|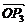 |=1,
|=1,
∴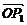 ·
·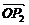 =-
=-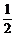 .
.
∴|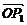 ||
||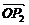 |cos∠P1OP2=-
|cos∠P1OP2=-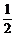 ,
,
即∠P1OP2=120°.
同理∠P1OP3=∠P2OP3=120°.
∴△P1P2P3为等边三角形.
评述:解本题的关键是由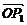 +
+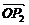 +
+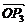 =0转化出现向量的数量积,进而求夹角.
=0转化出现向量的数量积,进而求夹角.
深化拓展
本题也可用如下方法证明:以O点为坐标原点建立直角坐标系,设P1(x1,y1),P2(x2,y2),P3(x3,y3),
则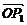 =(x1,y1),
=(x1,y1),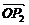 =(x2,y2),
=(x2,y2),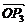 =(x3,y3).
=(x3,y3).
由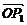 +
+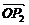 +
+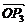 =0,
=0,
得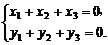 ∴
∴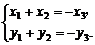
由|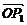 |=|
|=|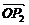 |=|
|=|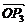 |=1,得x12+y12=x22+y22=x32+y32=1.
|=1,得x12+y12=x22+y22=x32+y32=1.
∴2+2(x1x2+y1y2)=1.
∴|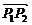 |=
|=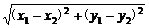
=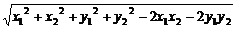
=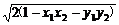 =
=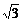 .
.
同理|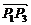 |=
|=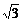 ,|
,|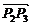 |=
|=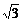 .
.
∴△P1P2P3为正三角形.
●闯关训练
夯实基础
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com