
5.设a+b+c=1,a2+b2+c2=1且a>b>c.
求证:-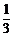 <c<0.
<c<0.
证明:∵a2+b2+c2=1,
∴(a+b)2-2ab+c2=1.
∴2ab=(a+b)2+c2-1=(1-c)2+c2-1=2c2-2c.
∴ab=c2-c.
又∵a+b=1-c,
∴a、b是方程x2+(c-1)x+c2-c=0的两个根,且a>b>c.
令f(x)=x2+(c-1)x+c2-c,则
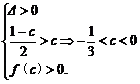
4.已知a+b+c=0,求证:ab+bc+ca≤0.
证法一:(综合法)∵a+b+c=0,
∴(a+b+c)2=0.
展开得ab+bc+ca=-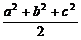 ,
,
∴ab+bc+ca≤0.
证法二:(分析法)要证ab+bc+ca≤0,
∵a+b+c=0,
故只需证ab+bc+ca≤(a+b+c)2,
即证a2+b2+c2+ab+bc+ca≥0,
亦即证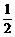 [(a+b)2+(b+c)2+(c+a)2]≥0.
[(a+b)2+(b+c)2+(c+a)2]≥0.
而这是显然的,由于以上相应各步均可逆,
∴原不等式成立.
证法三:∵a+b+c=0,∴-c=a+b.
∴ab+bc+ca=ab+(b+a)c=ab-(a+b)2
=-a2-b2-ab=-[(a+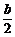 )2+
)2+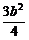 ]≤0.
]≤0.
∴ab+bc+ca≤0.
培养能力
3.已知a>b>c且a+b+c=0,求证: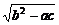 <
<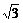 a.
a.
证明:要证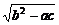 <
<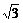 a,只需证b2-ac<3a2,
a,只需证b2-ac<3a2,
即证b2+a(a+b)<3a2,即证(a-b)(2a+b)>0,
即证(a-b)(a-c)>0.
∵a>b>c,∴(a-b)·(a-c)>0成立.
∴原不等式成立.
2.对实数a和x而言,不等式x3+13a2x>5ax2+9a3成立的充要条件是____________.
解析:(x3+13a2x)-(5ax2+9a3)
=x3-5ax2+13a2x-9a3
=(x-a)(x2-4ax+9a2)
=(x-a)[(x-2a)2+5a2]>0.
∵当x≠2a≠0时,有(x-2a)2+5a2>0.
由题意故只需x-a>0即x>a,以上过程可逆.
答案:x>a
1.已知a、b是不相等的正数,x=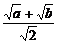 ,y=
,y=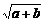 ,则x、y的关系是
,则x、y的关系是
A.x>y B.y>x C.x>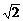 y D.不能确定
y D.不能确定
解析:∵x2=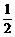 (
(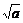 +
+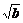 )2=
)2=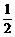 (a+b+2
(a+b+2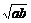 ),
),
y2=a+b=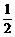 (a+b+a+b)>
(a+b+a+b)>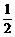 (a+b+2
(a+b+2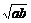 )=x2,又x>0,y>0.∴y>x.
)=x2,又x>0,y>0.∴y>x.
答案:B
5.若a>b>c,则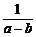 +
+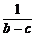 _______
_______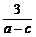 .(填“>”“=”“<”)
.(填“>”“=”“<”)
解析:a>b>c,(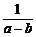 +
+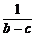 )(a-c)=(
)(a-c)=(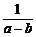 +
+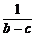 )[(a-b)+(b-c)]
)[(a-b)+(b-c)]
≥2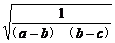 ·2
·2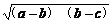 =4.
=4.
∴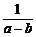 +
+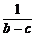 ≥
≥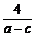 >
>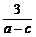 .
.
答案:>
●典例剖析
[例1] 设实数x、y满足y+x2=0,0<a<1.求证:loga(ax+ay)<loga2+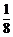 .
.
剖析:不等式左端含x、y,而右端不含x、y,故从左向右变形时应消去x、y.
证明:∵ax>0,ay>0,
∴ax+ay≥2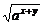 =2
=2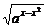 .
.
∵x-x2=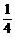 -(x-
-(x-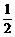 )2≤
)2≤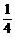 ,0<a<1,
,0<a<1,
∴ax+ay≥2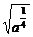 =2a
=2a .
.
∴loga(ax+ay)<loga2a =loga2+
=loga2+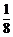 .
.
评述:本题的证题思路可由分析法获得.要证原不等式成立,只要证ax+ay≥2·a 即可.
即可.
[例2] 已知a、b、c∈R+,且a+b+c=1.求证:
(1+a)(1+b)(1+c)≥8(1-a)(1-b)(1-c).
剖析:在条件“a+b+c=1”的作用下,将不等式的“真面目”隐含了,给证明不等式带来困难,若用“a+b+c”换成“1”,则还原出原不等式的“真面目”,从而抓住实质,解决问题.
证明:∵a、b、c∈R+且a+b+c=1,
∴要证原不等式成立,
即证[(a+b+c)+a]·[(a+b+c)+b][(a+b+c)+c]≥8[(a+b+c)-a]·[(a+b+c)-b]·[(a+b+c)-c].
也就是证[(a+b)+(c+a)][(a+b)+(b+c)]·[(c+a)+(b+c)]≥8(b+c)(c+a)(a+b). ①
∵(a+b)+(b+c)≥2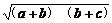 >0,
>0,
(b+c)+(c+a)≥2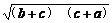 >0,
>0,
(c+a)+(a+b)≥2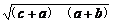 >0,
>0,
三式相乘得①式成立.
故原不等式得证.
[例3] 已知a>1,n≥2,n∈N*.
求证: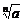 -1<
-1<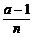 .
.
证法一:要证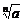 -1<
-1<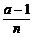 ,
,
即证a<(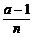 +1)n.
+1)n.
令a-1=t>0,则a=t+1.
也就是证t+1<(1+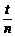 )n.
)n.
∵(1+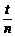 )n=1+C
)n=1+C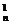
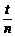 +…+C
+…+C (
(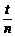 )n>1+t,
)n>1+t,
即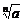 -1<
-1<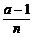 成立.
成立.
证法二:设a=xn,x>1.
于是只要证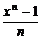 >x-1,
>x-1,
即证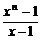 >n.联想到等比数列前n项和1+x+…+xn-1=
>n.联想到等比数列前n项和1+x+…+xn-1=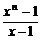 , ①
, ①
倒序xn-1+xn-2+…+1=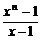 . ②
. ②
①+②得2·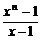 =(1+xn-1)+(x+xn-2)+…+(xn-1+1)
=(1+xn-1)+(x+xn-2)+…+(xn-1+1)
>2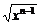 +2
+2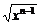 +…+2
+…+2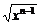 >2n.
>2n.
∴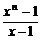 >n.
>n.
思考讨论
本不等式是与自然数有关的命题,用数学归纳法可以证吗?读者可尝试一下.
●闯关训练
夯实基础
4.(理)在等差数列{an}与等比数列{bn}中,a1=b1>0,an=bn>0,则am与bm的大小关系是____________.
解析:若d=0或q=1,则am=bm.
若d≠0,画出an=a1+(n-1)d与bn=b1·qn-1的图象,
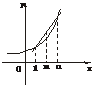
易知am>bm,故am≥bm.
答案:am≥bm
(文)在等差数列{an}与等比数列{bn}中,a1=b1>0,a2n+1=b2n+1>0(n=1,2,3,…),则an+1与bn+1的大小关系是____________.
解析:an+1=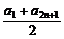 ≥
≥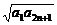 =
=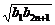 =bn+1.
=bn+1.
答案:an+1≥bn+1
3.分析法是从要证的不等式出发,寻求使它成立的
A.充分条件 B.必要条件
C.充要条件 D.既不充分又不必要条件
答案:A
2.(2003年南京市质检题)若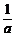 <
<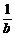 <0,则下列结论不正确的是
<0,则下列结论不正确的是
A.a2<b2 B.ab<b2
C.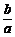 +
+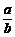 >2 D.|a|+|b|>|a+b|
>2 D.|a|+|b|>|a+b|
解析:由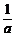 <
<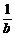 <0,知b<a<0.
<0,知b<a<0.
∴A不正确.
答案:A
1.(2005年春季北京,8)若不等式(-1)na<2+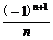 对任意n∈N*恒成立,则实数a的取值范围是
对任意n∈N*恒成立,则实数a的取值范围是
A.[-2,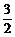 ) B.(-2,
) B.(-2,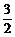 )
)
C.[-3,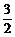 ) D.(-3,
) D.(-3,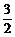 )
)
解析:当n为正偶数时,
a<2-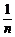 ,2-
,2-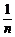 为增函数,
为增函数,
∴a<2-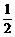 =
=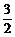 .
.
当n为正奇数时,-a<2+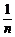 ,a>-2-
,a>-2-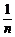 .
.
而-2-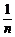 为增函数,-2-
为增函数,-2-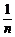 <-2,
<-2,
∴a≥-2.故a∈[-2,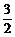 ).
).
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com