
1.本节重点问题是证明三点共线、三线共点以及求异面直线所成的角.
9.如下图,已知空间四边形ABCD的对角线AC=10,BD=6,M、N分别是AB、CD的中点,MN=7,求异面直线AC与BD所成的角.
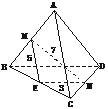
解:取BC的中点E,连结EN、EM,
∴∠MEN是异面直线AC与BD所成的角或其补角.
在△EMN中,EN=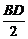 =3,EM=
=3,EM=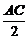 =5,MN=7,cos∠MEN=-
=5,MN=7,cos∠MEN=-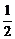 ,∴∠MEN=120°.
,∴∠MEN=120°.
∴异面直线AC与BD所成的角是60°.
●思悟小结
8.如下图,设△ABC和△A1B1C1的三对对应顶点的连线AA1、BB1、CC1相交于一点O,且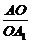 =
=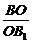 =
=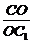 =
= 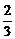 .试求
.试求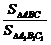 的值.
的值.
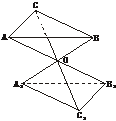
解:依题意,因为AA1、BB1、CC1相交于一点O,且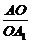 =
=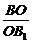 =
=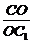 ,所以AB∥A1B1,AC∥A1C1,BC∥B1C1.由平移角定理得∠BAC=∠B1A1C1,∠ABC=∠A1B1C1,△ABC∽
,所以AB∥A1B1,AC∥A1C1,BC∥B1C1.由平移角定理得∠BAC=∠B1A1C1,∠ABC=∠A1B1C1,△ABC∽
△A1B1C1,所以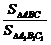 =(
=(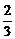 )2=
)2=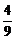 .
.
说明:利用平移定理,可证明空间两个角相等或两个三角形相似、全等;利用平行公理,可证明空间两条直线平行,从而解决相关问题.
探究创新
7.如下图,在三棱锥P-ABC中,AB=AC,PB=PC,E、F分别是PC和AB上的点且PE∶EC=AF∶FB=3∶2.
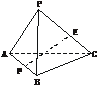
(1)求证:PA⊥BC;
(2)设EF与PA、BC所成的角分别为α、β,求证:α+β=90°.
证明:(1)取BC的中点D,连结AD、PD.
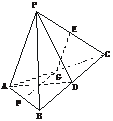
则BC⊥平面ADP,AP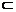 平面ADP,
平面ADP,
∴AP⊥BC.
(2)在AC上取点G,使AG∶GC=3∶2,连结EG、FG,则EG∥PA,FG∥BC,从而∠EGF为PA与BC所成的角,由(1)知∠EGF=90°,而∠GEF、∠GFE分别是EF与PA、EF与BC所成的角α、β,∴α+β=90°.
6.在三棱锥A-BCD中,AD=BC=2a,E、F分别是AB、CD的中点,EF=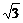 a,求AD与BC所成的角.
a,求AD与BC所成的角.
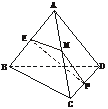
解:取AC的中点M,连结ME、MF,则ME∥BC,MF∥AD,所以∠EMF(或其补角)是直线AD与BC所成的角.在△EMF中,ME=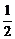 BC=a,MF=
BC=a,MF=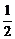 AD=a,EF=
AD=a,EF=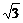 a,cos∠EMF=
a,cos∠EMF=
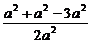 =-
=-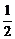 ,∠EMF=120°,因此异面直线AD与BC所成的角为60°.
,∠EMF=120°,因此异面直线AD与BC所成的角为60°.
培养能力
5.如下图,设不全等的△ABC与△A1B1C1不在同一平面内,且AB∥A1B1,BC∥B1C1,CA∥C1A1.
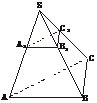
求证:AA1、BB1、CC1三线共点.
证明:不妨设AB≠A1B1,AA1∩BB1=S,∵BC∥B1C1,∴BB1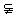 面BCC1B1,S∈面BBC1B1.同理,S∈面ACC1A1.∴S∈CC1,即AA1、BB1、CC1三线共点于S.
面BCC1B1,S∈面BBC1B1.同理,S∈面ACC1A1.∴S∈CC1,即AA1、BB1、CC1三线共点于S.
4.(2003年上海)在正四棱锥P-ABCD中,若侧面与底面所成二面角的大小为60°,则异面直线PA与BC所成角的大小等于_____________.(结果用反三角函数值表示)
答案:arctan2
3.如下图,四面体ABCD中,E、F分别是AC、BD的中点,若CD=2AB=2,EF⊥AB,则EF与CD所成的角等于_____________.
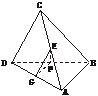
解析:取AD的中点G,连结EG、FG,易知EG=1,FG=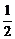 .
.
由EF⊥AB及GF∥AB知EF⊥FG.
在Rt△EFG中,求得∠GEF=30°,即为EF与CD所成的角.
答案:30°
2.(2004年天津,6)如下图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于
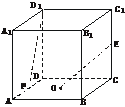
A.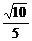 B.
B.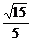 C.
C.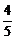 D.
D.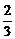
解法一:取面CC1D1D的中心为H,连结FH、D1H.在△FHD1中,
FD1=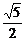 ,FH=
,FH=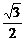 ,D1H=
,D1H=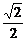 .
.
由余弦定理,得∠D1FH的余弦值为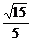 .
.
解法二:取BC的中点G.连结GC1∥FD1,再取GC的中点H,连结HE、OH,则∠OEH为异面直线所成的角.
在△OEH中,OE=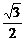 ,HE=
,HE=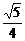 ,OH=
,OH=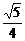 .
.
由余弦定理,可得cos∠OEH=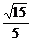 .
.
答案:B
1.两条相交直线l、m都在平面α内且都不在平面β内.命题甲:l和m中至少有一条与β相交,命题乙:平面α与β相交,则甲是乙的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.非充分非必要条件
解析:若l和m中至少有一条与β相交,不妨设l∩β=A,则由于l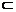 α,∴A∈α.而A∈β,∴α与β相交.反之,若α∩β=a,如果l和m都不与β相交,由于它们都不在平面β内,
α,∴A∈α.而A∈β,∴α与β相交.反之,若α∩β=a,如果l和m都不与β相交,由于它们都不在平面β内,
∴l∥β且m∥β.∴l∥a且m∥a,进而得到l∥m,与已知l、m是相交直线矛盾.因此l和m中至少有一条与β相交.
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com