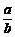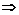3.作商法：a＞0，b＞0，＞1a＞b.

特别提示

2.比较法：a－b＞0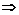a＞b，a－b＜0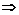a＜b.

1.均值定理：a+b≥2；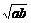

ab≤(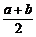)²(a、b∈R⁺)，

当且仅当a=b时取等号.

6.2　 不等式的证明(一)

●知识梳理

3.强化函数的性质在大小比较中的重要作用，加强知识间的联系.

拓展题例

[例1] 已知f(x)=|log₂(x+1)|，m＜n，f(m)=f(n).

(1)比较m+n与0的大小；

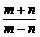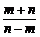(2)比较f()与f()的大小.

剖析：本题关键是如何去掉绝对值号，然后再判断差的符号.

解：(1)∵f(m)=f(n)，

∴|log₂(m+1)|=|log₂(n+1)|.

∴log₂²(m+1)=log₂²(n+1).

∴［log₂(m+1)+log₂(n+1)］［log₂(m+1)－log₂(n+1)］=0，

log₂(m+1)(n+1)·log₂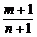=0.

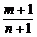∵m＜n，∴≠1.

∴log₂(m+1)(n+1)=0.

∴mn+m+n+1=1.∴mn+m+n=0.

当m、n∈(－1，0］或m、n∈［0，+∞)时，

由函数y=f(x)的单调性知x∈(－1，0］时，f(x)为减函数，x∈［0，+∞)时，f(x)为增函数，f(m)≠f(n).

∴－1＜m＜0，n＞0.∴m·n＜0.

∴m+n=－mn＞0.

(2)f(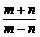)=|log₂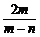|=－l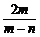og₂=log₂，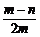

f(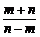)=|log₂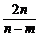|=log₂.

－=

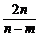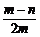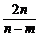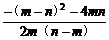
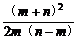=－＞0.

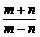∴f()＞f().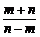

[例2] 某家庭准备利用假期到某地旅游，有甲、乙两家旅行社提供两种优惠方案，甲旅行社的方案是：如果户主买全票一张，其余人可享受五五折优惠；乙旅行社的方案是：家庭旅游算集体票，可按七五折优惠.如果甲、乙两家旅行社的原价相同，请问该家庭选择哪家旅行社外出旅游合算？

解：设该家庭除户主外，还有x人参加旅游，甲、乙两旅行社收费总金额分别为y₁和y₂.一张全票价格为a元，

那么y₁=a+0.55ax，y₂=0.75(x+1)a.

∴y₁－y₂=a+0.55ax－0.75a(x+1)=0.2a(1.25－x).

∴当x＞1.25时，y₁＜y₂；

当x＜1.25时，y₁＞y₂.又因x为正整数，

所以当x=1，即两口之家应选择乙旅行社；

当x≥2(x∈N)，即三口之家或多于三口的家庭应选择甲旅行社.

2.通过复习要强化不等式“运算”的条件.如a＞b、c＞d在什么条件下才能推出ac＞bd.

1.加强化归意识，把比较大小问题转化为实数的运算.

4.对于含参问题的大小比较要注意分类讨论.

●教师下载中心

教学点睛

3.对两个(或两个以上)不等式同加(或同乘)时一定要注意不等式是否同向(且大于零).

2.一定要在理解的基础上记准、记熟不等式的性质，并注意解题中灵活、准确地加以应用.