
6.求y=1+sinx+cosx+sinxcosx的值域.
解:设t=sinx+cosx,则t∈[-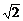 ,
,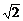 ].
].
由(sinx+cosx)2=t2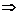 sinxcosx=
sinxcosx=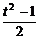 .
.
∴y=1+t+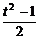 =
=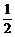 (t+1)2.
(t+1)2.
∴ymax=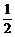 (
(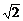 +1)2=
+1)2=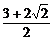 ,ymin=0.
,ymin=0.
∴值域为[0,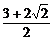 ].
].
培养能力
5.(2004年湖南,13)已知向量a=(cosθ,sinθ),向量b=(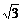 ,-1),则|2a-b|的最大值是____________.
,-1),则|2a-b|的最大值是____________.
解析:∵2a-b=(2cosθ-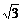 ,2sinθ+1),
,2sinθ+1),
∴|2a-b|=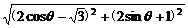 =
=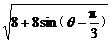 ≤4.
≤4.
∴|2a-b|的最大值为4.
答案:4
4.在△ABC中,a=sin(A+B),b=sinA+sinB,则a与b的大小关系为_______.
解析:a=sinAcosB+cosAsinB<sinA+sinB=b.
答案:a<b
3.函数y=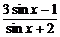 的最大值是_______,最小值是_______.
的最大值是_______,最小值是_______.
解析:∵y=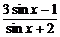 =
=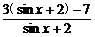 =3-
=3-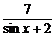 ,
,
∴当sinx=1时,ymax=3-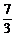 =
=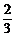 ;
;
当sinx=-1时,ymin=-4.
答案: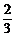 -4
-4
2.当y=2cosx-3sinx取得最大值时,tanx的值是
A.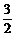 B.-
B.-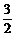 C.
C.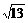 D.4
D.4
解析:y=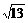 sin(
sin(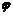 -x)(其中tan
-x)(其中tan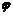 =
=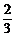 ).y有最大值时,应sin(
).y有最大值时,应sin(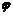 -x)=1
-x)=1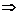
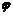 -x=2kπ+
-x=2kπ+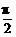
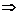 -x=2kπ+
-x=2kπ+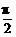 -
-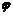 .
.
∴tanx=-tan(-x)=-tan(2kπ+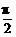 -
-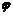 )=-cot
)=-cot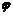 =-
=-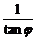 =-
=-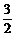 .
.
答案:B
1.函数y=log2(1+sinx)+log2(1-sinx),当x∈[-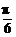 ,
,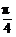 ]时的值域为
]时的值域为
A.[-1,0] B.(-1,0]
C.[0,1) D.[0,1]
解析:y=log2(1-sin2x)=log2cos2x.
当x=0时,ymax=log21=0;
当x=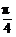 时,ymin=-1.∴值域为[-1,0].
时,ymin=-1.∴值域为[-1,0].
答案:A
5.y=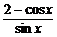 (0<x<π)的最小值是________.
(0<x<π)的最小值是________.
解析一:y=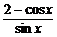
 ysinx+cosx=2
ysinx+cosx=2
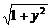 sin(x+
sin(x+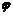 )=2
)=2
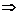 sin(x+
sin(x+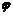 )=
)=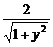 (x∈(0,π))
(x∈(0,π))
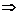 0<
0<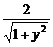 ≤1
≤1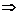 y≥
y≥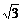 .
.
∴ymin=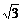 .
.
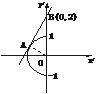
解析二:y可视为点A(-sinx,cosx),B(0,2)连线的斜率kAB,而点A的轨迹
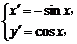 x∈(0,π)是单位圆在第二、三象限的部分(如下图),易知当A(-
x∈(0,π)是单位圆在第二、三象限的部分(如下图),易知当A(-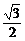 ,
,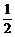 )时,ymin=kAB=
)时,ymin=kAB=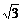 .
.
答案: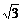
●典例剖析
[例1] 函数y=acosx+b(a、b为常数),若-7≤y≤1,求bsinx+acosx的最大值.
剖析:函数y=acosx+b的最值与a的符号有关,故需对a分类讨论.
解:当a>0时,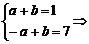 a=4,b=-3;
a=4,b=-3;
当a=0时,不合题意;
当a<0时,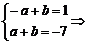 a=-4,b=-3.
a=-4,b=-3.
当a=4,b=-3时,bsinx+acosx=-3sinx+4cosx=5sin(x+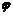 )(tan
)(tan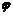 =-
=-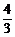 );
);
当a=-4,b=-3时,bsinx+acosx=-3sinx-4cosx=5sin(x+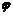 )(tan
)(tan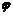 =
=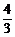 ).
).
∴bsinx+acosx的最大值为5.
[例2] 求函数y=cot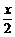 sinx+cotxsin2x的最值.
sinx+cotxsin2x的最值.
剖析:先将切函数化成弦函数,再通过配方转化成求二次函数的最值问题.
解:y=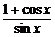 ·sinx+
·sinx+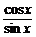 ·2sinxcosx
·2sinxcosx
=2(cosx+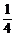 )2+
)2+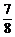 .
.
∵sinx≠0,∴cosx≠±1.
∴当cosx=-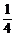 时,y有最小值
时,y有最小值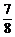 ,无最大值.
,无最大值.
评述:这是个基本题型,解题时要注意式中的隐含条件.
[例3] 求函数y=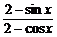 的最大值和最小值.
的最大值和最小值.
剖析:此题的解法较多,一是利用三角函数的有界性;二是数形结合法,将y看成是两点连线的斜率;三是利用万能公式换算,转化成一元函数的最值问题(由于万能公式不要求掌握,所以此方法只作了解即可).
解法一:去分母,原式化为
sinx-ycosx=2-2y,
即sin(x-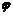 )=
)=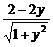 .
.
故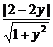 ≤1,解得
≤1,解得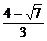 ≤y≤
≤y≤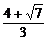 .
.
∴ymax=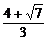 ,ymin=
,ymin=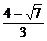 .
.
解法二:令x1=cosx,y1=sinx,有x12+y12=1.它表示单位圆,则所给函数y就是经过定点P(2,2)以及该圆上的动点M(cosx,sinx)的直线PM的斜率k,故只需求此直线的斜率k的最值即可.由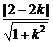 =1,得k=
=1,得k=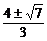 .
.
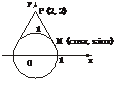
∴ymax=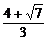 ,ymin=
,ymin=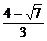 .
.
评述:数形结合法是高考中必考的数学思维方法,对此读者要有足够的重视.
●闯关训练
夯实基础
4.y=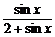 的最大值是_________,最小值是_________.
的最大值是_________,最小值是_________.
解析一:y=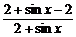 =1-
=1-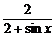 .
.
当sinx=-1时,得ymin=-1,
当sinx=1时,得ymax=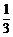 .
.
解析二:原式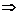 sinx=
sinx=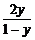 (∵y≠1)
(∵y≠1)
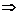 |
|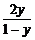 |≤1
|≤1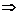 -1≤y≤
-1≤y≤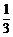 .
.
∴ymax=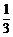 ,ymin=-1.
,ymin=-1.
答案: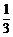 -1
-1
∴当x=-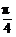 时,ymin=
时,ymin=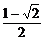 .
.
答案:D
3.函数y=x-sinx在[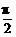 ,π]上的最大值是
,π]上的最大值是
A.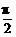 -1 B.
-1 B. +1
+1
C. -
-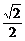 D.π
D.π
解析:y=x-sinx在[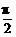 ,π]上是增函数,
,π]上是增函数,
∴x=π时,ymax=π.
答案:D
3.判断y=-Asin(ωx+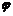 )(ω>0)的单调区间,只需求y=Asin(ωx+
)(ω>0)的单调区间,只需求y=Asin(ωx+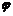 )的相反区间即可,一般常用数形结合.而求y=Asin(-ωx+
)的相反区间即可,一般常用数形结合.而求y=Asin(-ωx+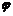 )(-ω<0)单调区间时,则需要先将x的系数变为正的,再设法求之.(读者考虑为什么)
)(-ω<0)单调区间时,则需要先将x的系数变为正的,再设法求之.(读者考虑为什么)
●教师下载中心
教学点睛
本节是图象和性质的综合应用的内容,例题讲解要突出数形结合思想、化归转化思想、分类讨论等数学思想方法,并注意三角知识的载体作用,注意和其他知识间的关联.
拓展题例
[例1] 判断f(x)=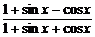 的奇偶性.
的奇偶性.
正确解法:取x=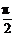 ,f(x)有意义,取x=-
,f(x)有意义,取x=-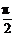 ,f(x)没有意义,故定义域关于原点不对称.
,f(x)没有意义,故定义域关于原点不对称.
∴f(x)是非奇非偶函数.
常见错误及诊断:一些学生不分析定义域是否关于原点对称,而急于函数变形,极易导致错误的结论.要注意判断奇偶性的步骤:一是分析定义域是否关于原点对称,二是分析f(x)与f(-x)的关系.
[例2] 在△ABC中,a、b、c成等比数列,求函数y=sinB+cosB的值域.
分析:b2=ac可转化为∠B的取值范围.
解:∵b2=ac,cosB=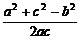 =
=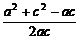 =
=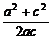 -
- ≥
≥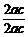 -
- =
= ,
,
∴B∈(0,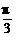 ].∴y=
].∴y=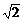 sin(B+
sin(B+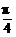 )∈(1,
)∈(1,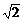 ].
].
拓展:如果a、b、c成等差数列呢?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com