
1.解含有绝对值的不等式的指导思想是去掉绝对值.常用的方法是:(1)由定义分段讨论;(2)利用绝对值不等式的性质;(3)平方.
9.(1)已知|a|<1,|b|<1,求证:|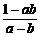 |>1;
|>1;
(2)求实数λ的取值范围,使不等式|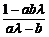 |>1对满足|a|<1,|b|<1的一切实数a、b恒成立;
|>1对满足|a|<1,|b|<1的一切实数a、b恒成立;
(3)已知|a|<1,若|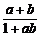 |<1,求b的取值范围.
|<1,求b的取值范围.
(1)证明:|1-ab|2-|a-b|2=1+a2b2-a2-b2=(a2-1)(b2-1).
∵|a|<1,|b|<1,∴a2-1<0,b2-1<0.
∴|1-ab|2-|a-b|2>0.
∴|1-ab|>|a-b|,
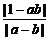 =
=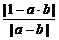 >1.
>1.
(2)解:∵|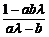 |>1
|>1 |1-abλ|2-|aλ-b|2=(a2λ2-1)(b2-1)>0.
|1-abλ|2-|aλ-b|2=(a2λ2-1)(b2-1)>0.
∵b2<1,∴a2λ2-1<0对于任意满足|a|<1的a恒成立.
当a=0时,a2λ2-1<0成立;
当a≠0时,要使λ2<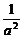 对于任意满足|a|<1的a恒成立,而
对于任意满足|a|<1的a恒成立,而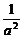 >1,
>1,
∴|λ|≤1.故-1≤λ≤1.
(3)|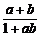 |<1
|<1 (
(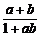 )2<1
)2<1 (a+b)2<(1+ab)2
(a+b)2<(1+ab)2 a2+b2-1-a2b2<0
a2+b2-1-a2b2<0 (a2-1)(b2-1)<0.
(a2-1)(b2-1)<0.
∵|a|<1,∴a2<1.∴1-b2>0,即-1<b<1.
●思悟小结
8.有点难度哟!
已知f(x)=x2-x+c定义在区间[0,1]上,x1、x2∈[0,1],且x1≠x2,求证:
(1)f(0)=f(1);
(2)| f(x2)-f(x1)|<|x1-x2|;
(3)|
f(x1)-f(x2)|<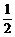 ;
;
(4)|
f(x1)-f(x2)|≤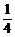 .
.
证明:(1)f(0)=c,f(1)=c,
∴f(0)=f(1).
(2)| f(x2)-f(x1)|=|x2-x1||x2+x1-1|.
∵0≤x1≤1,∴0≤x2≤1,0<x1+x2<2(x1≠x2).
∴-1<x1+x2-1<1.
∴| f(x2)-f(x1)|<|x2-x1|.
(3)不妨设x2>x1,由(2)知
| f(x2)-f(x1)|<x2-x1. ①
而由f(0)=f(1),从而
| f(x2)-f(x1)|=| f(x2)-f(1)+f(0)-f(x1)|≤| f(x2)-f(1)|+| f(0)-
f(x1)|<|1-x2|+|x1|<1-x2+x1. ②
①+②得2| f(x2)-f(x1)|<1,
即| f(x2)-f(x1)|<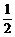 .
.
(4)|f(x2)-f(x1)|≤fmax-fmin=f(0)-f(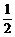 )=
)=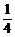 .
.
探究创新
7.(2003年湖北黄冈模拟题)已知函数f(x)=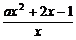 的定义域恰为不等式log2(x+3)+log
的定义域恰为不等式log2(x+3)+log x≤3的解集,且f(x)在定义域内单调递减,求实数a的取值范围.
x≤3的解集,且f(x)在定义域内单调递减,求实数a的取值范围.
解:由log2(x+3)+log x≤3得
x≤3得
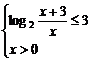
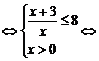 x≥
x≥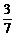 ,
,
即f(x)的定义域为[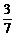 ,+∞).
,+∞).
∵f(x)在定义域[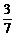 ,+∞)内单调递减,
,+∞)内单调递减,
∴当x2>x1≥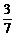 时,f(x1)-f(x2)>0恒成立,即有(ax1-
时,f(x1)-f(x2)>0恒成立,即有(ax1-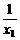 +2)-(ax2-
+2)-(ax2-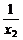 +2)>0
+2)>0 a(x1-x2)-(
a(x1-x2)-(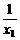 -
-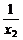 )>0
)>0
 (x1-x2)(a+
(x1-x2)(a+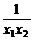 )>0恒成立.
)>0恒成立.
∵x1<x2,∴(x1-x2)(a+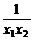 )>0
)>0
 a+
a+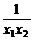 <0.
<0.
∵x1x2>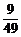
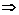 -
-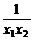 >-
>-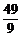 ,
,
要使a<-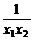 恒成立,
恒成立,
则a的取值范围是a≤-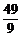 .
.
6.解不等式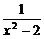 ≤
≤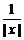 .
.
解:(1)当x2-2<0且x≠0,即当-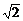 <x<
<x<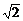 且x≠0时,原不等式显然成立.
且x≠0时,原不等式显然成立.
(2)当x2-2>0时,原不等式与不等式组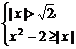 等价.
等价.
x2-2≥|x|,即|x|2-|x|-2≥0.
∴|x|≥2.∴不等式组的解为|x|≥2,
即x≤-2或x≥2.
∴原不等式的解集为(-∞,-2]∪(-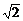 ,0)∪(0,
,0)∪(0,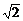 )∪[2,+∞).
)∪[2,+∞).
5.关于x的方程3x2-6(m-1)x+m2+1=0的两实根为x1、x2,若|x1|+|x2|=2,求m的值.
解:x1、x2为方程两实根,
∴Δ=36(m-1)2-12(m2+1)≥0.
∴m≥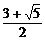 或m≤
或m≤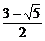 .
.
又∵x1·x2=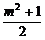 >0,∴x1、x2同号.
>0,∴x1、x2同号.
∴|x1|+|x2|=|x1+x2|=2|m-1|.
于是有2|m-1|=2,∴m=0或2.
∴m=0.
培养能力
4.(2004年春季北京)当0<a<1时,解关于x的不等式a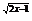 <ax-2.
<ax-2.
解:由0<a<1,原不等式可化为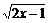 >x-2.
>x-2.
这个不等式的解集是下面不等式组①及②的解集的并集.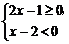 ①
①
或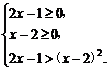 ②
②
解不等式组①得解集为{x|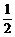 ≤x<2},
≤x<2},
解不等式组②得解集为{x|2≤x<5},
所以原不等式的解集为{x|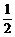 ≤x<5}.
≤x<5}.
3.(2004年全国Ⅰ,13)不等式|x+2|≥|x|的解集是____________.
解法一:|x+2|≥|x| (x+2)2≥x2
(x+2)2≥x2 4x+4≥0
4x+4≥0 x≥-1.
x≥-1.
解法二: 在同一直角坐标系下作出f(x)=|x+2|与g(x)=|x|的图象,根据图象可得x≥-1.
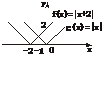
解法三:根据绝对值的几何意义,不等式|x+2|≥|x|表示数轴上x到-2的距离不小于到0的距离,∴x≥-1.
答案:{x|x≥-1}
评述:本题的三种解法均为解绝对值不等式的基本方法,必须掌握.
2.不等式|x2+2x|<3的解集为____________.
解析:-3<x2+2x<3,即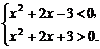
∴-3<x<1.
答案:-3<x<1
1.(2003年北京海淀区一模题)已知集合A={x|a-1≤x≤a+2},B={x|3<x<5},则能使A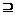 B成立的实数a的取值范围是
B成立的实数a的取值范围是
A.{a|3<a≤4} B.{a|3≤a≤4}
C.{a|3<a<4} D.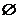
解析:由题意知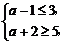 得3≤a≤4.
得3≤a≤4.
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com