
题目列表(包括答案和解析)
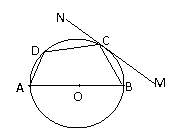
3、过.圆内接四边形ABCD的顶点C引切线MN,
AB为圆直径,若∠BCM=380,则∠ADC=
A.1420 B. 1280 C. 1120 D. 1380
1、 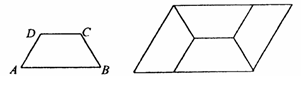 如图甲,四边形
如图甲,四边形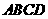 是等腰
是等腰
梯形,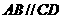 .由4个这样的
.由4个这样的
等腰梯形可以拼出图乙所示 甲 乙
的平行四边形, 则四边形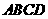 中
中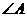 度数为 ( )
度数为 ( )
A.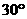 B.
B.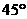 C.
C. D.
D.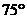
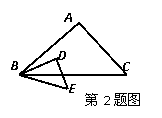 2如图,在
2如图,在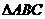 和
和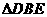 中,
中,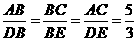 ,若
,若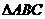
与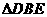 的周长之差为
的周长之差为 ,则
,则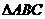 的周长为( )
的周长为( )
 A.
A.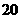
 B.
B.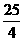
 C.
C.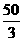
 D.25
D.25
24.(本小题满分10分)若正数 、
、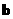 满足
满足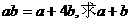 的取值范围。
的取值范围。 

23.(本小题满分10分)
已知曲线C1: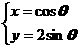
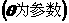 ,曲线C2:y=x+1。
,曲线C2:y=x+1。 

(1)指出C1是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1上各点的纵坐标都压缩为原来的一半,得到曲线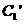 ,试写出
,试写出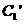 的参数方程,并判断
的参数方程,并判断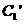 与C2的位置关系。
与C2的位置关系。
22.(本小题满分10分)已知m∈R,直线l: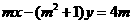 和曲线C:
和曲线C: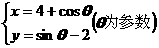 。
。
(1)求直线l斜率的取值范围; 

(2)直线l能否将曲线C分割成弧长的比值为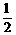 的两段圆弧?为什么?
的两段圆弧?为什么?
21.(本小题满分12分) 罐中有5个红球,3个白球,从中每次任取一球后放入一个红球,直到取到红球为止用ε表示抽取次数,求ε的分布列,并计算P(1<ε≤3). 

20.(本小题满分12分)有人玩掷硬币走跳跳棋的游戏,已知硬币出现正反面的概率都是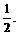 棋盘上标有第0站、第1站、第2站、…第100站. 一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次:若掷出正面,棋向前跳一站(从k到k+1);若掷出反面,棋子向前跳二站(从k到k+2),直到棋子跳到第99站(胜利大本营)或跳到第100站(失败集中营)时,该游戏结束. 设棋子跳到第n站的概率为
棋盘上标有第0站、第1站、第2站、…第100站. 一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次:若掷出正面,棋向前跳一站(从k到k+1);若掷出反面,棋子向前跳二站(从k到k+2),直到棋子跳到第99站(胜利大本营)或跳到第100站(失败集中营)时,该游戏结束. 设棋子跳到第n站的概率为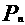 。
。 

(1)求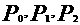 的值;
的值;
(2)求证: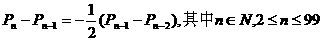 ;
;
(3)求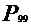 及
及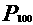 的值.
的值.
19.(本小题满分12分) 袋中有4个白球和5个黑球,连续从中取出3个球,计算: 

(1)“取后放回,且顺序为黑白黑”的概率;(2)“取后不放回,且取出2黑1白”的概率。
18. (本小题满分12分)有6名同学站成一排,求:(1)甲不站排头也不站排尾有多少种不同的排法;(2)甲不站排头,且乙不站排尾有多少种不同的排法;(3)甲、乙、丙不相邻有多少种不同的排法。 

17.(本小题满分12分) 已知: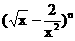 的展开式中,第五项与第三项的二项式系数之比为14:3,求:展开式的常数项和中间项。
的展开式中,第五项与第三项的二项式系数之比为14:3,求:展开式的常数项和中间项。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com