
题目列表(包括答案和解析)
6.有5名学生站列成一列,要求甲同学必须站在乙同学的后面(可以不相邻),则不同的站法有
A.120种 B.60种 C.48种 D.150种
5.三棱追P-ABC的侧棱PA、PB、PC两两垂直,若三个侧面面积分别是6,4,3,则此三棱追的体积是
A.4 B.6 C.8 D.10
4.(理科做)在三棱锥的六条棱中任意选择两条,则这两条棱恰好是一对一面直线的概率为
A.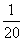 B.
B.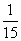 C.
C.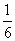 D.
D.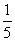
4.(文科做)用简单随机抽样从含有8个个体的总体中抽取一个容量为2的样本。抽样过程中个体a恰好在第二次被抽到的概率为
A.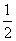 B.
B.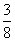 C.
C. D.
D.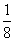
3.3封投入4个邮箱里,投放一共有
A.4种 B.24种 C.81种 D.64种
2.两男两女4个同学排成一排照相,如果要求男女相间而立,那么满足条件的站法共有
A.4种 B.8种 C.12种 D.6种
1.某学校有教职工100人,其中一线教师80人,后勤管理20人,现从中选取10人组成一
个考察团外出学习考察,则这10人中恰好有8名教师的不同选法种数是
A.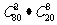 B.
B.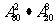 C
C
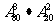 D
D

22. 解:
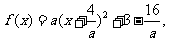 所有
所有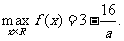
(1)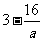 >5,即
>5,即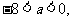 时,
时,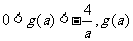 是方程
是方程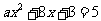 较小的根,即
较小的根,即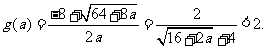
(2)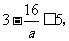 即
即 时,
时,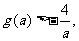 且
且 所以
所以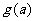 是方程
是方程 较大根,即
较大根,即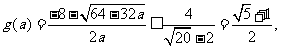 当且仅当
当且仅当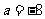 时,等号成立.
时,等号成立.
由于 ,因此当且仅当
,因此当且仅当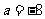 时,
时,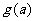 取最大值
取最大值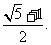
21.解:
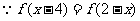 ,则函数图像关于
,则函数图像关于 对称,
对称,
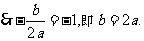 ①
①
由条件(3)得: 时,
时, ②
②
由条件(1)得: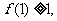 由条件(2)得
由条件(2)得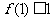 .
.
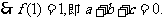 ③
③
由①②③,得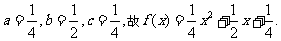
假设存在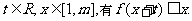
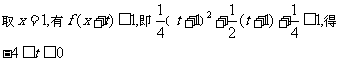
对固定的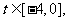 取
取 ,有
,有 ,
,
即 化简为
化简为

解得
即当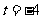 时对任意的
时对任意的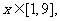 恒有
恒有
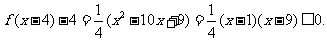
即 恒成立.
恒成立. 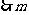 的最大值为9.
的最大值为9.
20. 解:
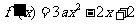
(1)
当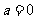 时,
时,
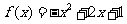
则其单调递增区间为
(2)
当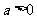 时,
时,
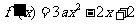 开口向上,下面讨论
开口向上,下面讨论 .
.
当 时,即
时,即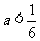 ,两根为
,两根为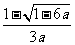 ,
,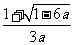
此时原函数的单调递增区间是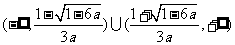
当 时,即
时,即 恒大于等于零,故而原函数单调递增区间是
恒大于等于零,故而原函数单调递增区间是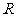
(3)
当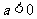 时,
时,
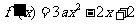 开口向下,下面讨论
开口向下,下面讨论 .
.
当 时,即
时,即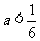 ,两根为
,两根为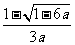 ,
,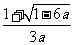
此时原函数的单调递增区间是
当 时,即
时,即 恒小于等于零,故而原函数无单调递增区间.
恒小于等于零,故而原函数无单调递增区间.
综上, 当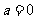 时,单调递增区间为
时,单调递增区间为
当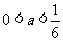 时,单调递增区间是
时,单调递增区间是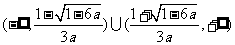
当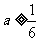 时,单调递增区间是
时,单调递增区间是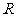 .
.
当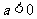 时,单调递增区间是
时,单调递增区间是 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com