
题目列表(包括答案和解析)
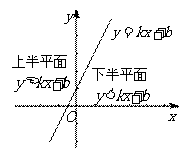
6.不等式表示的平面区域:
一般地,直线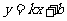 把平面分成两个区域:
把平面分成两个区域:
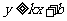 表示直线及直线上方的平面区域;
表示直线及直线上方的平面区域;
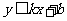 表示直线及直线下方的平面区域.
表示直线及直线下方的平面区域.
注:对于不含边界的区域,要将边界画成虚线.
3.解不等式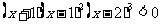
(7)无理不等式:转化时把握二点:一是两边非负才能平方,二是根式必须有意义.
①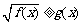
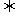 等价于
等价于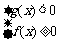 或
或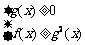 ;
;
②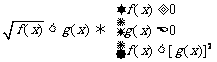 ;
;
③ ;
;
④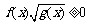 型,应按
型,应按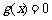 和
和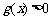 进行分类.
进行分类.
(8)指数、对数不等式:转化时把握“同底数原则”“单调性原则”,同时还要注意真数大于零,底数要使不等式有意义.
①当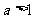 时
时
 ;
; 
②当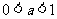 时
时
 ;
; 
 (9)含参数的不等式:合理分类是关键,根据零根、根式有意义、影响不等号方向等因素确定分类标准,分类时要做到不重、不漏,然后求解并分类作答.
(9)含参数的不等式:合理分类是关键,根据零根、根式有意义、影响不等号方向等因素确定分类标准,分类时要做到不重、不漏,然后求解并分类作答.
2.解不等式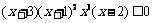 ,
,
由图知不等式的解集为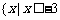 或
或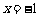 或
或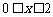 },
},
 (注意“等号”须单独考虑)
(注意“等号”须单独考虑)
5.不等式的解法: 注意“系数化正”
(1)一元一次不等式: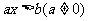 ;
; 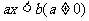
(2)一元二次不等式: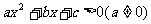
(“系数化正”,根据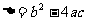 的三种情况(
的三种情况( )写出解集.)
)写出解集.)
解一元二次不等式的步骤: (1)二次项系数化为正数; (2)解对应的一元二次方程;
(3)根据一元二次方程的根,结合不等号的方向画图;(4)写出不等式的解集. 一元二次不等式恒成立小结:
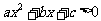 (
(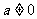 )恒成立
)恒成立
 .
. 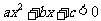 (
(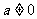 )恒成立
)恒成立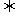
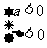
(3)绝对值不等式:若 ,则
,则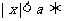
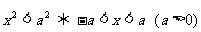 ;
;
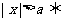
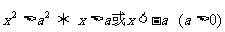 ;
;
注:(ⅰ)去绝对值符号的方法:
① 平方法:通过两边平方去绝对值;需要注意的是不等号两边须为非负值.
②
讨论法:讨论绝对值中式子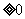 还是
还是 ,然后去绝对值符号,转化为一般不等式.
,然后去绝对值符号,转化为一般不等式.
③等价转化法:如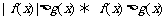 或
或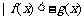 ;
;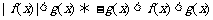 .
.
(ⅱ)含有多个绝对值符号的不等式可用“按零点分区间讨论”的方法来解.
转化时利用 “零点分段法”(找零点,分段讨论,去掉绝对值符号,最后取各段的并集.)
如:解不等式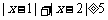 ,由两个零点
,由两个零点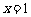 及
及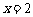 将R分为三段去掉绝对值再求解,
将R分为三段去掉绝对值再求解,
每一段的解都是不等式的解,最后取并集.
(ⅲ)绝对值不等式: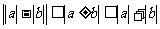
(4) 连不等式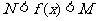 的转化:
的转化:
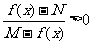
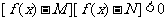
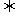
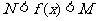
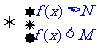
(5) 分式不等式的解法:分式不等式变形为整式不等式;
⑴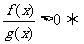
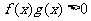 ;⑵
;⑵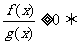
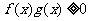
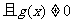 ;
;
注:①分式不等式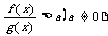 解法:
解法:
(移项通分,分子分母因式分解,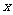 的系数化为1,用穿轴法求结果)
的系数化为1,用穿轴法求结果)
②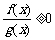 等价于
等价于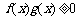 且
且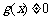 .对于“等号”要慎重处理.
.对于“等号”要慎重处理.
(6)高次不等式:方法 “序轴标根法” (变形→标根→穿线→定解)
①不等式转化为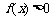 (
(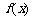 系数为1,根由小到大排列),
系数为1,根由小到大排列),
②将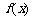 分解为若干一次因式或二次不可分因式的乘积(使各括号内
分解为若干一次因式或二次不可分因式的乘积(使各括号内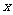 的系数为正),再将各根有序的标在数轴上,
的系数为正),再将各根有序的标在数轴上,
③利用“奇穿偶回”(奇偶指幂指数的次数)的原则求解不等式.
用“穿轴法”解高次不等式技巧:“奇穿,偶切”(穿轴时从最大根的右上方开始)
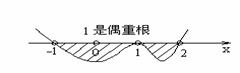
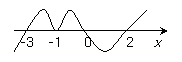
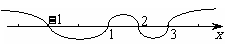 如: 1. 解不等式
如: 1. 解不等式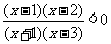 ,
,
解:原不等式等价于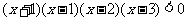 ,
,
将方程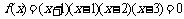 的根
的根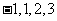 标在
标在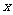 轴上,
轴上,
从右到左画出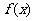 的示意图,∴原不等式的解集是
的示意图,∴原不等式的解集是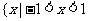 或
或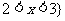 .
.
4.作差法证明不等式步骤:
⑴作差;⑵变形(对差进行因式分解或配方变成几个数(式)的完全平方和);⑶判断差的符号.
3.均值不等式:若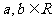 ,则
,则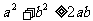 (当且仅当
(当且仅当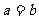 时取等号)
时取等号)
若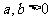 ,则
,则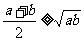 (当且仅当
(当且仅当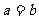 时取等号)
时取等号)
基本变形:①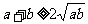 ;
;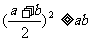 (当且仅当a=b时取“=”号)
(当且仅当a=b时取“=”号)
②若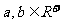 ,则
,则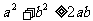 ;
;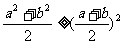 .
.
求最值时注意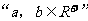 且“等号成立”时的条件,积
且“等号成立”时的条件,积 或和
或和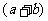 其中之一为定值.
其中之一为定值.
应用条件:“①一正二定三相等;②积定和小,和定积大”.
注:①两个正数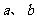 的调和平均数、几何平均数、算术平均数、均方根之间的关系是:
的调和平均数、几何平均数、算术平均数、均方根之间的关系是: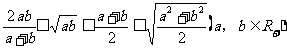 当且仅当
当且仅当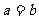 时等号成立.
时等号成立.
②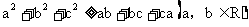 当且仅当
当且仅当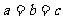 时取等号.
时取等号.
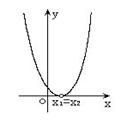
2.一元二次不等式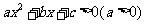 与相应的二次函数
与相应的二次函数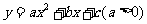 、
、
相应的一元二次方程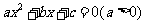 之间的关系:
之间的关系:
判别式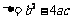 |
 |
 |
 |
二次函数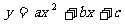 ( ( )的图象 )的图象 |
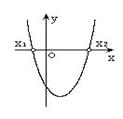 |
 |
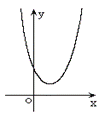 |
一元二次方程 |
有两相异实根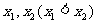 |
有两相等实根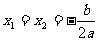 |
无实根 |
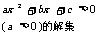 |
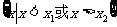 |
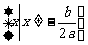 |
R |
 |
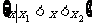 |
 |
 |
2.两个不等式相乘时,必须注意同向同正时才能相乘,即同向同正可乘;同时要注意“同号可倒”即a>b>o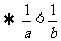 ,a<b<o
,a<b<o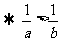 .
.
1.不等式的基本性质:填空题采用“特殊值法”处理
(1)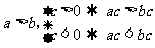 (2)
(2)
(3)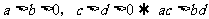 (4)
(4)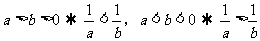
(5)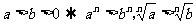
(6)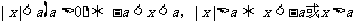
注:1.求不等式的解集、定义域及值域时,结果一定要用集合或区间表示,不能用不等式表示.
6.(2004四川模拟)在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共有__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com