
题目列表(包括答案和解析)
5. (湖北卷)设数列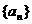 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,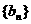 为等比数列,且
为等比数列,且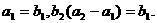
(Ⅰ)求数列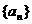 和
和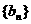 的通项公式;
的通项公式;
(Ⅱ)设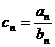 ,求数列
,求数列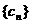 的前n项和Tn.
的前n项和Tn.
解:(1):当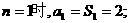
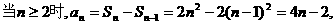
故{an}的通项公式为 的等差数列.
的等差数列.
设{bn}的通项公式为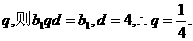
故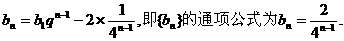
(II)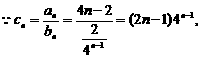
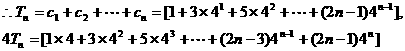
两式相减得
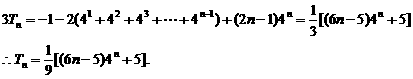
4. (福建卷)已知数列{an}满足a1=a, an+1=1+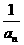 我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列:
我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列:
(Ⅰ)求当a为何值时a4=0;
(Ⅱ)设数列{bn}满足b1=-1,
bn+1=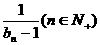 ,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};
,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};
(Ⅲ)若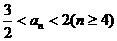 ,求a的取值范围.
,求a的取值范围.
(I)解法一: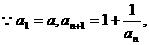

故a取数列{bn}中的任一个数,都可以得到一个有穷数列{an}
3.(福建卷)
已知{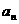 }是公比为q的等比数列,且
}是公比为q的等比数列,且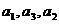 成等差数列.
成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{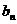 }是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
解:(Ⅰ)由题设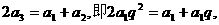
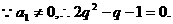
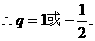
(Ⅱ)若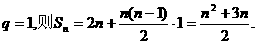
当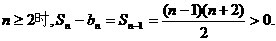 故
故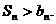
若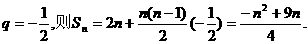
当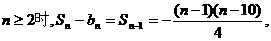
故对于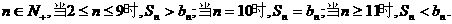
2.(北京卷)数列{an}的前n项和为Sn,且a1=1,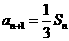 ,n=1,2,3,……,求
,n=1,2,3,……,求
(I)a2,a3,a4的值及数列{an}的通项公式;
(II)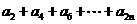 的值.
的值.
解:(I)由a1=1,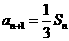 ,n=1,2,3,……,得
,n=1,2,3,……,得
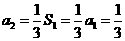 ,
,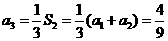 ,
,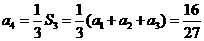 ,
,
由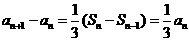 (n≥2),得
(n≥2),得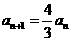 (n≥2),
(n≥2),
又a2=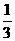 ,所以an=
,所以an=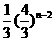 (n≥2),
(n≥2),
∴ 数列{an}的通项公式为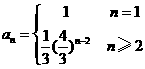 ;
;
(II)由(I)可知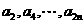 是首项为
是首项为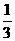 ,公比为
,公比为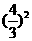 项数为n的等比数列,∴
项数为n的等比数列,∴ 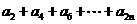 =
=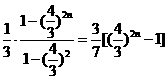
1.(北京卷)
设数列{an}的首项a1=a≠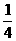 ,且
,且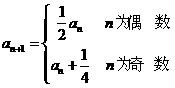 ,
,
记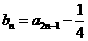 ,n==l,2,3,…·.
,n==l,2,3,…·.
(I)求a2,a3;
(II)判断数列{bn}是否为等比数列,并证明你的结论;
(III)求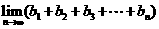 .
.
解:(I)a2=a1+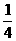 =a+
=a+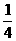 ,a3=
,a3=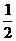 a2=
a2=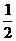 a+
a+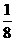 ;
;
(II)∵ a4=a3+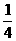 =
=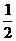 a+
a+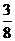 , 所以a5=
, 所以a5=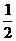 a4=
a4=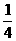 a+
a+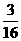 ,
,
所以b1=a1-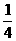 =a-
=a-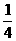 , b2=a3-
, b2=a3-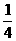 =
=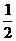 (a-
(a-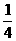 ), b3=a5-
), b3=a5-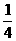 =
=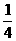 (a-
(a-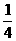 ),
),
猜想:{bn}是公比为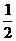 的等比数列·
的等比数列·
证明如下:
因为bn+1=a2n+1-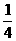 =
=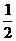 a2n-
a2n-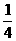 =
=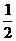 (a2n-1-
(a2n-1-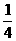 )=
)=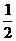 bn, (n∈N*)
bn, (n∈N*)
所以{bn}是首项为a-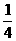 , 公比为
, 公比为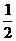 的等比数列·
的等比数列·
(III)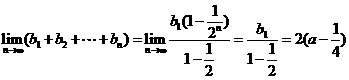 .
.
10. (重庆卷)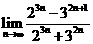 = -3
.
= -3
.
解答题
9. (天津卷)在数列{an}中, a1=1,
a2=2,且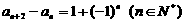 ,
,
则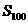 =_2600_ ___.
=_2600_ ___.
8. (天津卷)设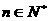 ,则
,则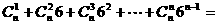
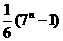
7、计算: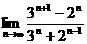 =_3 _________。
=_3 _________。
6. (上海)12、用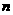 个不同的实数
个不同的实数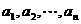 可得到
可得到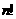 个不同的排列,每个排列为一行写成一个
个不同的排列,每个排列为一行写成一个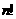 行的数阵。对第
行的数阵。对第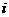 行
行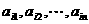 ,记
,记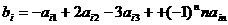 ,
,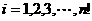 。例如:用1,2,3可得数阵如图,由于此数阵中每一列各数之和都是12,所以,
。例如:用1,2,3可得数阵如图,由于此数阵中每一列各数之和都是12,所以,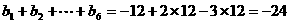 ,那么,在用1,2,3,4,5形成的数阵中,
,那么,在用1,2,3,4,5形成的数阵中,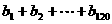 =_-1080_________。
=_-1080_________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com