
题目列表(包括答案和解析)
22.(本题满分14分)在10件产品中有2件次品,连续抽3次,每次抽1件,
(1)在放回抽样的情况下,求抽到次品数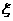 的分布列和
的分布列和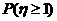 ;
;
(2)在不放回抽样的情况下,求抽到次品数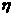 的分布列,并
的分布列,并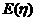 .
.
23 (本题满分14分)在四面体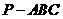 中,
中, ,
,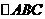 为正三角形,
为正三角形,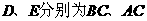 的中点,设
的中点,设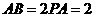 。
。
(1)如何在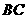 上找一点
上找一点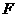 ,使
,使 ?请说明理由;
?请说明理由;
(2)求点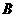 到面
到面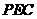 的距离;
的距离;
(3)对于(1)中的点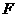 ,求二面角
,求二面角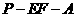 的大小.
的大小.
24 (本题满分14分)已知动点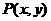 到定直线
到定直线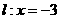 与定点
与定点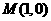 的距离相等.
的距离相等.
(1)求动点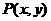 的轨迹方程;
的轨迹方程;
(2)记定直线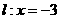 与
与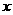 轴的交点为
轴的交点为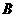 ,(1)中的轨迹方程上两点
,(1)中的轨迹方程上两点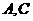 满足条件:
满足条件:
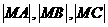 成等差数列,求弦
成等差数列,求弦 中点的横坐标;
中点的横坐标;
(3)设(2)中弦 的垂直平分线方程为
的垂直平分线方程为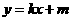 ,求
,求 的取值范围.
的取值范围.
25 (本题满分6分)试构造:
(1)一个周期为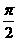 且是偶函数的三角函数;
且是偶函数的三角函数;
(2)一个在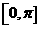 上单调增且为奇函数的三角函数.
上单调增且为奇函数的三角函数.
21.(本题满分14分)某公司年初花费72万元购进一台设备, 并立即投入使用. 计划第一年维护费用为8万元,从第二年开始,每一年所需维护费用比上一年增加4万元。现已知设备使用后,每年创造的收入为46万元,如果设备使用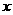 年后的累计盈利额为
年后的累计盈利额为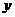 万元。求:
万元。求:
(1)写出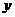 与
与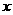 之间的函数关系式;(累计盈利额=累计收入-累计维护费-设备购置费)
之间的函数关系式;(累计盈利额=累计收入-累计维护费-设备购置费)
(2)从第几年开始,该设备开始盈利(即累计盈利额为正值)?
(3)使用若干年后,对该设备的处理方案有两种:当年平均盈利额达到最大值时,以42万元价格处理该设备;当累计盈利额达到最大值时,以10万元的价格处理该设备,问哪种处理方法较为合算?请说明你的理由.
20. (本题满分8分)已知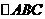 中,满足
中,满足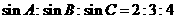 .试判断
.试判断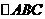 是什么形状?
是什么形状?
19. (本题满分8分)解不等式:
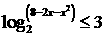
18. 椭圆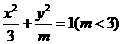 的离心率是方程
的离心率是方程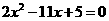 的根,则
的根,则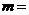 .
.
17. 由数字0,1,2,3组成的没有重复数字的四位偶数共有 .
16. 方程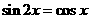 在区间
在区间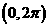 内的解的个数为
.
内的解的个数为
.
15. 若函数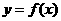 的图象经过点
的图象经过点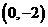 ,则函数
,则函数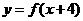 的图象必经过点 .
的图象必经过点 .
14. 设等比数列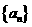 满足
满足 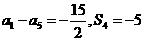 ,则公比
,则公比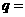 .
.
13.已知复数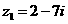 ,
,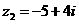 ,则
,则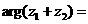 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com