
题目列表(包括答案和解析)
(1)记有限元素集合A的元素个数为n(A),A ={1,2,3}时,n(A)=3,若I是全集,M、N是其子集,且n(Ⅰ)=8,n(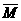 ∩N)=3,n(M∩N)=1,n(
∩N)=3,n(M∩N)=1,n(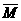 ∩
∩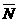 )=2,则n(M)=B
)=2,则n(M)=B
(A)4 (B)3 (C)2 (D)1
(2)若函数y =f(x)的图象和y =sin(x+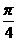 )的图象关于点A(
)的图象关于点A(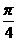 ,0)对称,则f(x)的表达式是B
,0)对称,则f(x)的表达式是B
(A)cos(x+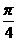 ) (B)-cos(x-
) (B)-cos(x-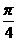 )
)
(C)-cos(x+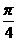 ) (D)cos(x-
) (D)cos(x-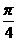 )
)
(3)一个圆锥的侧面展开图扇形的周长为2,则这个圆锥侧面积的最大值是C
(A)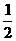 (B)
(B)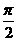 (C)
(C)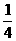 (D)
(D)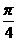
(4)如图,虚线部分是四个象限的角平分线,实线部分是函数y=f(x)的图象,则f(x)只能是D
(A) 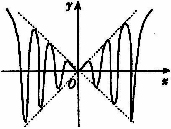 xsin
xsin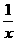
(B) xcos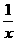
(C) x2sin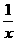
(D)x2cos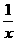
(5)在一定的条件下,某种细胞经过1小时1个分裂为2个,已知一定数量的细胞经过20个小时的分裂,细胞的个数成为230个,那么分裂到215个细胞需要B
(A)1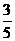 小时 (B)5小时 (C)2小时 (D)1
小时 (B)5小时 (C)2小时 (D)1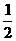 小时
小时
(6)在△ABC中,a2+b2=d·c2,且ctgC=1000(ctgA+ctgB),则常数d的值等于C
(A)1999 (B)2000 (C)2001 (D)2002
(7)已知圆(x-3)2+(y+4)2=r2上至多有两点到直线4x -3y –4 = 0的距离为1,则半径r的取值范围是B
(A)(0,4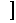 (B)(0,5) (C)(0,5
(B)(0,5) (C)(0,5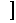 (D)[5,+∞]
(D)[5,+∞]
(8)某公司从2000年起,每人的年工资由三个项目组成并按下表规定实施C
|
项目 |
计算办法 |
|
基础工资 |
2000年1万元,考虑物价因素,以后每年递增10% |
|
住房补贴 |
按工龄计算:400元×工龄(工龄计算方法,如某职工1998年进公司,到2001年按4年计算) |
|
医疗费 |
每年1600元,固定不变 |
该公司的一职工在2002年将得到的住房补贴和医疗费之和可超过基础工资的25%,这位职工的工龄至少是
(A)2年 (B)3年 (C)4年 (D)5年
(9)设Sn为等差数列{an}的前n项和,S9=18,an-4=30(n>9),Sn=336,则n的值为B
(A)16 (B)21 (C)2 (D)18
(10)若不等式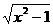 ≤
≤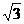 ax的解集为{x|1≤x≤2},则实数a的取值集合为A
ax的解集为{x|1≤x≤2},则实数a的取值集合为A
(A){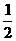 } (B){1} (C){a|a>4} (D){a|a>
} (B){1} (C){a|a>4} (D){a|a>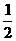 }
}
(11)对于函数f(x),在同一坐标系中,y1=f(x-19)与y2=f(99-x)的图象恒关于( C )对称
(A)y轴 (B)直线x =19 (C)直线x =59 (D)直线x =99
(12)函数f(x)=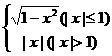 ,如果方程f(x)=a有且只有一个实根,那么a满足C
,如果方程f(x)=a有且只有一个实根,那么a满足C
(A)a<0 (B)0≤a<1 (C)a=1 (D)a>1
(13)一个等差数列共有3n项,它的前2n项的和为100,后2n项的和为200,则该等差数列的中间n项的和为 75 .
(14)将10个完全相同的小球放入编号为1、2、3的三个盒子内,要求每个盒子的球数不小于它的编号数,则不同的放法共 52 种.
(15)边长为6cm、8cm的矩形ABCD沿对角线折成60°的二面角后,过这四个顶点的球的表面积为 100 .
(16)不等式log2(x2-x)<3+x-x2的解为 (-1,0)∪(1,2) .
(1)下列各式中,值为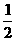 的是C
的是C
(A)sin15°cos15°
(B)2cos2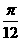 -1
-1
(C)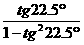 (D)
(D)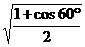
(2)已知条件甲:y=|x|,条件乙:点M(x,y)到两坐标轴距离相等,则甲是乙的A
(A)充分非必要条件 (B)必要非充分条件
(C)充要条件 (D)既不充分也不必要条件
(3)已知数列{an}的通项公式是an=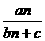 ,其中a,b,c均为正数,那么an与
,其中a,b,c均为正数,那么an与
an+1的大小是B
(A)an>an+1 (B)an<an+1
(C)an=an+1 (D)与n的取值有关
(4)若函数f(x)的图象与函数g(x)=2x-1的图象关于点(0,1)对称,则f(x)=B
(A)-2x+3 (B)-(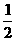 )x+3
)x+3
(C)2x+1 (D)(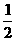 )x+1
)x+1
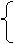 x=rsinθ
x=rsinθ
(5)方程
y=-1+rcosθ
(r为参数,θ为常数且|θ|<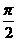 )所表示的图形是D
)所表示的图形是D
(A)以点(0,-1)为圆心,半径为|r|的圆的一部分
(B)以点(-1,0)为圆心,半径为|r|的圆的一部分
(C)过点(0,-1),倾斜角为θ的直线
(D)过点(0,-1),倾斜角为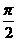 -θ的直线
-θ的直线
(6)两个母线长相等的圆锥,它们的侧面展开图恰好拼成一个圆面,且它们的侧面积之比为1∶2,则它们的高的比为C
(A)2∶1 (B)8∶5 (C)2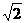 ∶
∶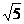 (D)2∶
(D)2∶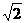
(7)在复平面内有五个点与方程x5=-1+i的五个根对应,则这五个点中有两个点在D
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(8)以椭圆的右焦点F2为圆心的圆恰好过椭圆的中心,交椭圆于点M、N,椭圆的左焦点为F1,且直线MF1与此圆相切,则椭圆的离心率e为D
(A)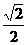 (B)
(B)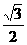 (C)2-
(C)2-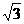 (D)
(D)
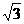 -1
-1
(9)已知二次函数f(x)=4x2-2(p-2)x-2p2-p+1,若区间[-1,1]内至少存在一个实数c,使f(c)>0,则实数p的范围是C
(A)(-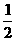 ,1) (B)(-3,-
,1) (B)(-3,-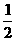 )
)
(C)(-3,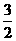 ) (D)(-
) (D)(-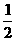 ,
,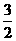 )
)
(10)已知f(x)是偶函数,它在[0,+∞)上是减函数,若f(lgx)>f(1),则x的取值范围是C
(A)(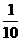 ,1) (B)(0,
,1) (B)(0,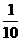 )∪(1,+∞)
)∪(1,+∞)
(C)(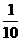 ,10) (D)(0,1)∪(10,+∞)
,10) (D)(0,1)∪(10,+∞)
(11)已知f(x)=sin2ωx-cos2ωx(ω>0)的最小正周期为1,则B
(A)ω=1,f(x)在[-π,0]上是增函数,f(x)是偶函数
(B)ω=π,f(x)在[-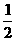 ,0]上是减函数,f(x)是偶函数
,0]上是减函数,f(x)是偶函数
(C)ω=1,f(x)在[-π,0]上是减函数,f(x)是奇函数
(D)ω=π,f(x)在[-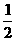 ,0]上是增函数,f(x)是奇函数
,0]上是增函数,f(x)是奇函数
(12)某体育彩票规定,从01至36共36个号码中抽出7个号为一注,每注2元.某人想从01至10中选3个连续的号,从11至20中选2个连续的号,从21至30中选1个号,从31至36中选1个号组成一注,则这人把这种特殊要求的号买全,至少要花D
(A)3600元 (B)6720元 (C)4320元 (D)8640元
(13)若a +b +c
= 3,且a、b、c∈R+,则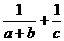 的最小值为 4/3 .
的最小值为 4/3 .
(14)若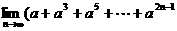 )≤1,则a =
)≤1,则a = 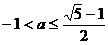 .
.
(15)复数z1满足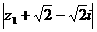 ≤1,复数z2满足
≤1,复数z2满足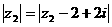 那么|z1-z2|的最小值为
那么|z1-z2|的最小值为 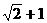 4
.
4
.
(16)不等式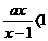 的解集为{x|x<1或x>2=,那么a的值为 1/2 .
的解集为{x|x<1或x>2=,那么a的值为 1/2 .
(1)在(-∞,0)上是增函数的是C
(A)y =x2+1 (B)y =-(x+1)2
(C)y =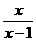 (D)y
=
(D)y
=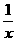
(2)在数列{an}中,a1=1,an+1=a2n-1,则此数列前4项之和为C
(A)1 (B)2 (C)0 (D)-1
(3)两圆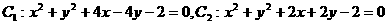 相交于P、Q两点,则下列各点在弦PQ所在直线上的是D
相交于P、Q两点,则下列各点在弦PQ所在直线上的是D
(A)(0,1) (B)(1,1) (C)(2,1) (D)(3,1)
(4)把函数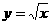 的图象上各点的横坐标扩大到原来的3倍,纵坐标也扩大到原来的3倍,则所得图象的解析式为C
的图象上各点的横坐标扩大到原来的3倍,纵坐标也扩大到原来的3倍,则所得图象的解析式为C
(A) 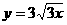 (B)
(B) 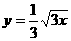 (C)
(C)  (D)
(D) 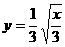
(5)在△ABC中,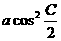 +
+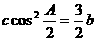 ,则A
,则A
(A)a、b、c成等差数列 (B)b、a、c成等差数列
(C)a、c、b成等差数列 (D)a =b =c
(6)a、b表示直线,α、β、γ表示平面,有下列四个命题:(1)若α∩β=a,b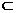 α,a⊥b,则α⊥β;(2)若α⊥β,α∩γ=a,β∩γ=b,则a⊥b;(3)若a不垂直于平面α,则a不可能垂直于α内的无数条直线;(4)若a⊥α,b⊥β,a∥b,则α∥β,其中不正确命题的个数为C
α,a⊥b,则α⊥β;(2)若α⊥β,α∩γ=a,β∩γ=b,则a⊥b;(3)若a不垂直于平面α,则a不可能垂直于α内的无数条直线;(4)若a⊥α,b⊥β,a∥b,则α∥β,其中不正确命题的个数为C
(A)1 (B)2 (C)3 (D)4
(7)设(a-b)n的展开式中,二项式系数的和为256,则此二项展开式中系数最小的项是A
(A)第5项 (B)第4、5两项
(C)第4、6两项 (D)第5、6两项
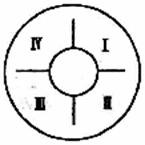
(8)中央电视台“正大综艺”节目的现场观众来自四个单位,分别在图中的四个区域内坐定.有四种不同颜色的服装,且相邻两个区域的颜色不同,不相邻区域的观众服装颜色相同与否,不受限制,那么不同的着装方法有B
(A)36种 (B)84种 (C)48种 (D)24种
(9)已知函数f(x)=x2-4x+5在[0,m]上的最大值为5,最小值为1,则m的取值范围为C
(A)[0,2] (B)[0,4]
(C)[2,4] (D)[0,+∞)
(10)一等边圆锥的底面圆周和顶点都在一个球的球面上,则此球与圆锥的体积之比为B
(A) 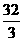 (B)
(B)
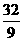 (C)
(C)
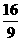 (D)
(D)
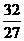
(11)抛物线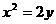 上距离点A(0,a)(a>0)最近的点恰好是顶点,这个结论成立的充要条件是D
上距离点A(0,a)(a>0)最近的点恰好是顶点,这个结论成立的充要条件是D
(A)a>0
(B)a≥1
(C)0<a≤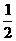 (D)0<a≤1
(D)0<a≤1
(12)设a>b>0,a +b =1,且x=logab,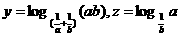 ,则x、y、z之间的大小关系为C
,则x、y、z之间的大小关系为C
(A)y<x<z (B)z<y<x (C)y<z<x (D)x<y<z
(13)对于给定的二个数3和3x,它们的等差中项a与等比中项b之间满足条件3a2=4b2,则正数b= 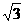 或
或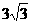 .
.
(14)设圆台的底面半径分别为1cm和7cm,如果该圆台的一个轴截面的两条对角线互相垂直,则这个圆台的侧面积为 80π .
(15)已知抛物线y2=2px(p>0),过焦点F的直线交抛物线于A、B两点,线段AB的中点为P,抛物线的准线为l,分别过A、B、P作x轴的平行线依次交l于M、N、Q,连FM、FN、FQ、AQ和BQ,则这些线段中互相垂直的有 AQ⊥BQ、BQ⊥NF、AQ⊥MF .(至少找出三对)
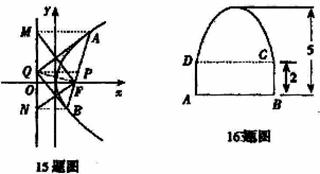
(16)设计一条单向行驶的公路隧道,需保证装有集装箱的汽车能够通过,如图所示隧道横断面由一段抛物线和矩形ABCD的三边组成,隧道高为5m,BC=2m,装有集装箱的汽车高4m,宽3m,不考虑其他因素,隧道底部的宽AB应至少设计为 5.2 m.(精确到0.1m)
(1)已知cosθ=cos60°,则θ等于C
(A)60° (B)k·360°+60°(k∈Z) (C)k·360°±60°(k∈Z) (D)k·180°+60°(k∈Z)
(2)设全集I=R,集合M={x|y=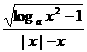 ,a>1},则
,a>1},则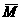 等于B
等于B
(A)(-∞,-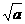 )
(B)[-
)
(B)[-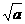 ,+∞ ) (C)(-
,+∞ ) (C)(-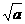 ,+∞) (D)(-∞,
,+∞) (D)(-∞, 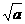 )
)
(3)如果圆柱的母线长为4,侧面积为8π,那么它的轴截面的一条对角线的长度为C
(A)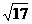 (B)
(B) 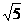 (C)2
(C)2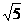 (D)4
(D)4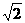
(4)在极坐标系中,经过极点,且与直线ρcosθ=2切于点M(2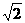 ,
,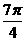 )的圆的方程是D
)的圆的方程是D
(A)ρ=4sinθ (B)ρ=2cosθ (C)ρ=-2cosθ (D)ρ=-4sinθ
(5)ω是正实数,函数f(x)=2sinωx在[-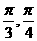 ,]上递增,那么A
,]上递增,那么A
(A)0<ω≤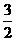 (B)0<ω≤2 (C)0<ω≤
(B)0<ω≤2 (C)0<ω≤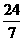 (D)ω≥2
(D)ω≥2
(6)如果把直线x-2y+λ=0先向左平移1个单位,再向下平移2个单位,使其
与圆x2+y2+2x-4y=0相切,则实数λ的值是A
(A)3,13 (B)-3,13 (C)3,-13 (D)-3,-13
(7)任取x1、x2∈[a,b]且x1≠x2,若f(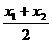 )>
)>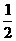 [f(x1)+f(x2)],则f(x)在[a,b]上是上凸函数,在以下图象中,是上凸函数的图象是D
[f(x1)+f(x2)],则f(x)在[a,b]上是上凸函数,在以下图象中,是上凸函数的图象是D
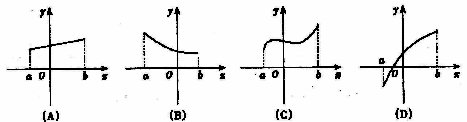
(8)已知函数f(x)=2arcsin(cosx)的定义域为(-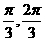 ,),则f(x)的值域是A
,),则f(x)的值域是A
(A)(-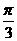 ,π)
(B)(-
,π)
(B)(-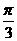 ,π) (C)(-
,π) (C)(-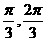 )
(D)(
)
(D)( 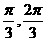 )
)
(9)已知k∈N,则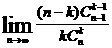 的值是D (A)
的值是D (A)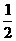 (B)
(B) 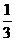 (C)2 (D)1
(C)2 (D)1
(10)α、β是两个不同的平面,m、n是平面α及β外的两条不同直线,给出四个论断:①m⊥n;②α⊥β;③n⊥β;④m⊥α,以其中三个结论作为条件,另一个论断作为结论,则所得命题正确的个数是B
 (A)1
(B)2
(C)3
(D)4
(A)1
(B)2
(C)3
(D)4
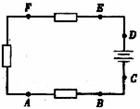
(11)如图,某电子器件是由三个电阻组成的回路,其中共有六个焊接点A、B、C、D、E、F,如果某个焊接点脱落,整个电路就会不通,现在发现电路不通了,那么焊接点脱落的可能性共有A
(A)63种 (B)64种 (C)6种 (D)36种
(12)设F1(-c,0)、F2(c,0)是椭圆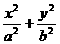 =1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则椭圆的离心率为B
=1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则椭圆的离心率为B
(A)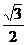 (B)
(B) 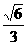 (C)
(C) 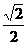 (D)
(D) 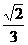
21.(14分)已知二次函数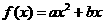 的图象过点
的图象过点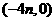 ,且
,且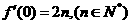
(1)求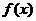 的解析式;
的解析式;
(2)若数列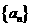 满足
满足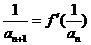 ,且
,且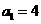 ,求数列
,求数列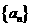 的通项公式;
的通项公式;
(3)对于(2)中的数列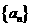 ,求证:①
,求证:①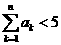 ;②
;②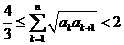 。
。
20.(13分)已知点A(1,0),B(0,1),C(1,1)和动点P(x,y)满足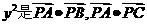 的等差中项. (1)求P点的轨迹方程;
的等差中项. (1)求P点的轨迹方程;
(2)设P点的轨迹为曲线C1按向量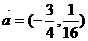 平移后得到曲线C2,曲线C2上不同的两点M,N的连线交y轴于点Q(0,b),如果∠MON(O为坐标原点)为锐角,求实数b的取值范围;
平移后得到曲线C2,曲线C2上不同的两点M,N的连线交y轴于点Q(0,b),如果∠MON(O为坐标原点)为锐角,求实数b的取值范围;
(3)在(2)的条件下,如果b=2时,曲线C2在点M和N处的切线的交点为R,求证:R在一条定直线上.
19. (12分)设函数f(x)=-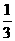 x3+2ax2-3a2x+
x3+2ax2-3a2x+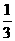 a(0<a<1)
a(0<a<1)
(1) 求函数f(x)的单调区间
(2)
若当x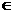 [a, 2]时,恒有f(x)≤0,试确定a的取值范围
[a, 2]时,恒有f(x)≤0,试确定a的取值范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com