
题目列表(包括答案和解析)
3.设l、m、n表示三条直线,α、β、γ表示三个平面,则下列命题中不成立的是( )
A.若l⊥α,m⊥α,则l∥m
B.若m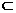 β,n是l在β内的射影,m⊥l,则m⊥n
β,n是l在β内的射影,m⊥l,则m⊥n
C.若m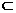 α,n
α,n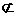 α,m∥n,则n∥α
α,m∥n,则n∥α
D.若α⊥γ,β⊥γ,则α∥β
2.将函数y=sinx按向量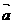 =(-
=(-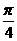 ,3)平移后的函数的解析式为 ( )
,3)平移后的函数的解析式为 ( )
A.y=sin(x-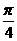 )+3 B.y=sin(x-
)+3 B.y=sin(x-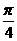 )-3
)-3
C.y=sin(x+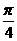 )+3 D.y=sin(x+
)+3 D.y=sin(x+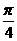 )-3
)-3
1.已知全集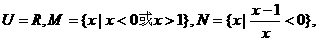 则 ( )
则 ( )
A.M∪N=R B.M∩N=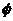 C.
C.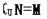 D.
D.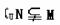
22.对于定义域为D的函数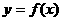 ,若同时满足:①
,若同时满足:①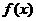 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[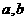 ]
]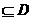 ,使
,使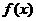 在[
在[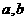 ]上的值域为[
]上的值域为[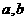 ];那么把
];那么把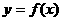 (
(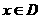 )叫闭函数。
)叫闭函数。
(1)求闭函数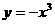 符合条件②的区间[
符合条件②的区间[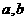 ];
];
(2)判断函数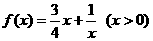 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若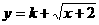 是闭函数,求实数
是闭函数,求实数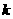 的取值范围。
的取值范围。
解:(1)由题意,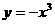 在[
在[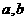 ]上递减,则
]上递减,则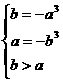 解得
解得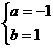
所以,所求的区间为[-1,1] ………………………(4分)
(2)取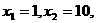 则
则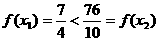 ,即
,即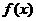 不是
不是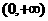 上的减函数。
上的减函数。
取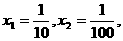
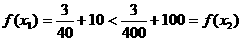 ,
,
即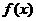 不是
不是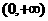 上的增函数
上的增函数
所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。…………(8分)
(3)若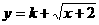 是闭函数,则存在区间[
是闭函数,则存在区间[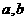 ],在区间[
],在区间[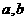 ]上,函数
]上,函数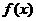 的值域为[
的值域为[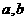 ],即
],即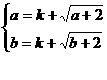 ,
,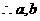 为方程
为方程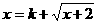 的两个实数根,
的两个实数根,
即方程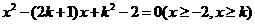 有两个不等的实根。………(10分)
有两个不等的实根。………(10分)
当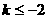 时,有
时,有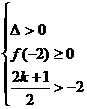 ,解得
,解得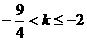 。
。
当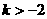 时,有
时,有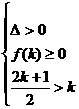 ,无解。
,无解。
综上所述,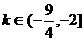 。………………………(14分)
。………………………(14分)
21.已知中心在原点的椭圆C的左焦点为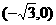 ,右顶点为(2,0).
,右顶点为(2,0).
(1)求椭圆C的方程;
(2)若直线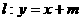 与椭圆C有两个不同的交点A和B,且
与椭圆C有两个不同的交点A和B,且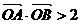 (其中O为原点), 求
实数m的取值范围.
(其中O为原点), 求
实数m的取值范围.
解:(Ⅰ)设椭圆方程为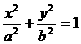
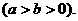
由已知得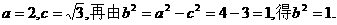
故椭圆C的方程为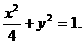 …………………………………4’
…………………………………4’
(Ⅱ)将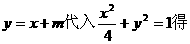
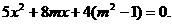
由直线l与椭圆C交于不同的两点得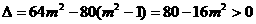
即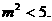 …………………………………8’
…………………………………8’
①
设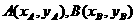 ,则
,则
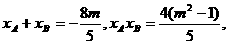 …………………………………10’
…………………………………10’

而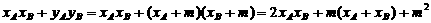
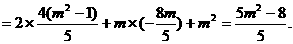
于是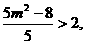 即
即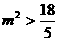 ② …………………………………12’
② …………………………………12’
由①、②得 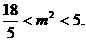
故m的取值范围为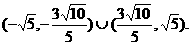 …………………………………14’
…………………………………14’
18.(12分)已知函数f(x)的图像与函数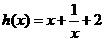 的图像关于点A(0,1)对称.
的图像关于点A(0,1)对称.
(1)求f(x)的解析式;
(2)若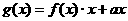 ,且
,且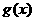 在区间(0,2)上为减函数,求实数a的取值范围;
在区间(0,2)上为减函数,求实数a的取值范围;
解:(1)设f(x)图像上任一点坐标为(x,y),点(x,y)关于点A(0,1)的对称点(-x,2-y)在h(x)图像上
∴ 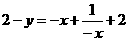 , ∴
, ∴ 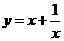 ,即
,即 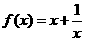 …………(6分)
…………(6分)
(2)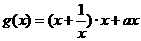 ,即
,即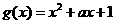
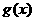 在(0,
在(0,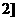 上递减
上递减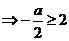 , ∴ a≤-4………………(12分)
, ∴ a≤-4………………(12分)
19(文).(本题12分) 等差数列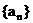 是递增数列,前n项和为
是递增数列,前n项和为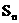 , 且
, 且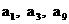 成等比数列,
成等比数列, 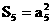
(1)求数列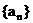 的通项公式;
的通项公式;
(2)若数列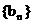 满足
满足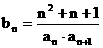 求数列
求数列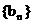 的前99项的和.
的前99项的和.
解:(1) 设数列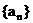 公差为
公差为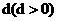
∵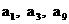 成等比数列 ∴
成等比数列 ∴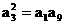 ………(1分)
………(1分)
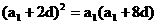 ………(3分)
………(3分)
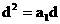 ∵
∵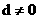 ∴
∴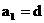 ……… ①………(4分)
……… ①………(4分)
∵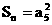 ∴
∴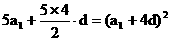 ……… ②………(5分)
……… ②………(5分)
由①②得: 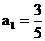
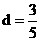 ∴
∴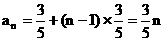 ………(7分)
………(7分)
(2) 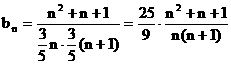
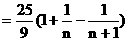 ………(9分)
………(9分)
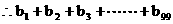
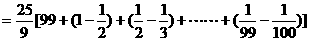
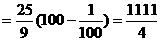 ………(12分)
………(12分)
19(理)、已知数列{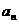 }中
}中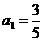 ,
,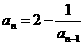 (n≥2,
(n≥2,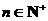 ),数列
),数列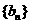 ,满足
,满足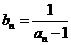
(1)求证数列{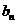 }是等差数列;(2)求数列{
}是等差数列;(2)求数列{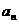 }中的最大项与最小项,并说明理由;
}中的最大项与最小项,并说明理由;
(3)记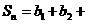 …
…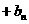 ,求lim
,求lim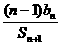
解: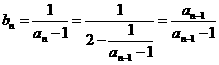 , ………………(2分)
, ………………(2分)
而 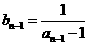 ,
,
∴ 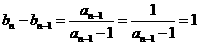 .
.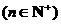
∴ {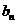 }是首项为
}是首项为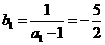 ,公差为1的等差数列.………………(4分)
,公差为1的等差数列.………………(4分)
(2)依题意有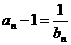 ,而
,而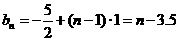 , ∴
, ∴ 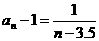 .
.
对于函数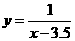 ,在x>3.5时,y>0,
,在x>3.5时,y>0,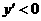 ,在(3.5,
,在(3.5, )上为减函数.
)上为减函数.
故当n=4时,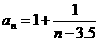 取最大值3………………(8分)
取最大值3………………(8分)
而函数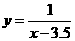 在x<3.5时,y<0,
在x<3.5时,y<0,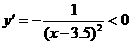 ,在(
,在(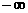 ,3.5)上也为减函数.
,3.5)上也为减函数.
故当n=3时,取最小值,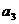 =-1.………………(10分)
=-1.………………(10分)
(3)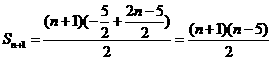 ,
,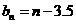 ,
,
∴ 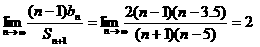 .………………(12分)
.………………(12分)
20(文).已知函数f(x)=-x3+3x2+ax+b在x=(1,f(1))处的切线与直线12x-y-1=0平行.
(1)求实数a的值;
(2)求f(x)的单调递减区间;
(3)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
解:(1) ∵f ’(x)=-3x2+6x+a …………………………………1’
∴f ’(1)=3+a=12,∴a=9 …………………………………3’
(2) f ’(x)=-3x2+6x+9.
令f ‘(x)<0,解得x<-1或x>3, …………………………………5’
所以函数f(x)的单调递减区间为(-∞,-1),(3,+∞).………………7’
(3)因为f(-2)=8+12-18+b=2+b,
f(2)=-8+12+18+b=22+b,
所以f(2)>f(-2). ……………………………8’
因为在(-1,3)上f ‘(x)>0,
所以f(x)在[-1, 2]上单调递增,又由于f(x)在[-2,-1]上单调递减,
因此f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值,
于是有 22+b=20,解得 b=-2. …………………………………10’
故f(x)=-x3+3x2+9x-2,因此f(-1)=1+3-9-2=-7,
即函数f(x)在区间[-2,2]上的最小值为-7. ………………………………12’
20(理).已知函数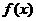 =
=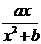 ,在
,在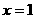 处取得极值2。 (1)求函数
处取得极值2。 (1)求函数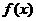 的解析式;
的解析式;
(2) 满足什么条件时,区间
满足什么条件时,区间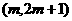 为函数
为函数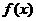 的单调增区间?
的单调增区间?
(3)若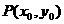 为
为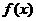 =
=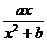 图象上的任意一点,直线
图象上的任意一点,直线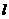 与
与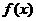 =
=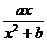 的图象切于
的图象切于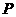 点,求直线
点,求直线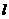 的斜率的取值范围。
的斜率的取值范围。
解:(1)已知函数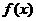 =
=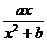 ,
,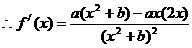 ………………(2分)
………………(2分)
又函数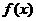 在
在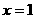 处取得极值2,
处取得极值2,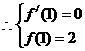 ,即
,即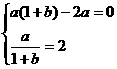
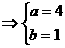
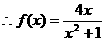 ………………………(4分)
………………………(4分)
(2)
由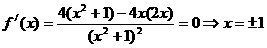
|
x |
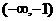 |
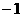 |
(-1,1) |
1 |
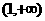 |
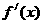 |
- |
0 |
+ |
0 |
|
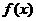 |
 |
极小值-2 |
 |
极大值2 |
 |
所以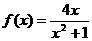 的单调增区间为
的单调增区间为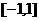 ,
………………………(6分)
,
………………………(6分)
若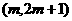 为函数
为函数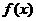 的单调增区间,则有
的单调增区间,则有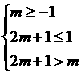
解得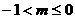
即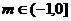 时,
时,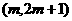 为函数
为函数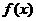 的单调增区间。 ………………………(8分)
的单调增区间。 ………………………(8分)
(3)
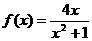

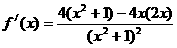
直线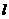 的斜率为
的斜率为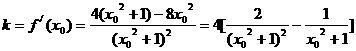 …………(10分)
…………(10分)
令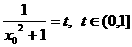 ,则直线
,则直线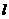 的斜率
的斜率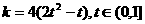 ,
,
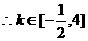 。
……………………(12分)
。
……………………(12分)
17、已知A(3,0),B(0,3),C(cosα,sinα).
(1)若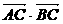 =-1,求sin2α的值;
=-1,求sin2α的值;
(2)若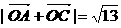 ,且α∈(0,π),求
,且α∈(0,π),求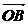 与
与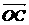 的夹角.
的夹角.
解:(1)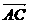 =(cosα-3,sinα),
=(cosα-3,sinα),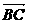 =(cosα,sinα-3),………………(2分)
=(cosα,sinα-3),………………(2分)
∴由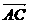 ·
·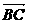 =-1,得(cosα-3)cosα+sinα(sinα-3)=-1,
=-1,得(cosα-3)cosα+sinα(sinα-3)=-1,
∴cosα+sinα=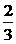 , ………………(4分)
, ………………(4分)
两边平方,得1+sin2α=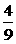 ,∴sin2α=-
,∴sin2α=-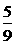 . …………(6分)
. …………(6分)
(2)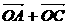 =(3+cosα,sinα),
=(3+cosα,sinα),
∴(3+cosα)2+sin2α=13, ∴cosα=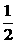 ,………………(8分)
,………………(8分)
∵α∈(0,π),∴α=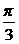 ,sinα=
,sinα=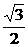 ,
,
∴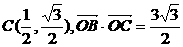 ,………………(10分)
,………………(10分)
设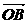 与
与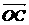 的夹角为θ,则cosθ=
的夹角为θ,则cosθ=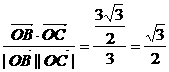
∴θ=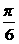 即为所求. ………………(12分)
即为所求. ………………(12分)
15.设函数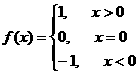 ,则方程
,则方程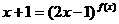 的解为 X=0,2或-
的解为 X=0,2或-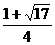 .
.
16 观察下列式子:
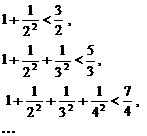 ,
,
则可以猜想的结论为:__ 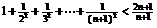 .或
.或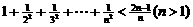 ._________________________.
._________________________.
14.函数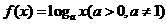 ,已知
,已知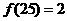 ,则
,则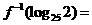 _
_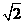 ________。
________。
13.某校高一、高二、高三三个年级的学生数分别为1500人、1200和1000人,现采用按年级分层抽样法了解学生的视力状况,已知在高一年级抽查了75人,则这次调查三个年级共抽查了 185 人.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com