
题目列表(包括答案和解析)
6. 已知数列{an}中,a1=8, a2 =4且满足an+1-2an+ an-1=0(n∈N*,n≥2),则数列{an}的前
30项的绝对值的和为( )
(A)870 (B)830 (C)1524 (D)1512
|
|
|
|
 7.已知
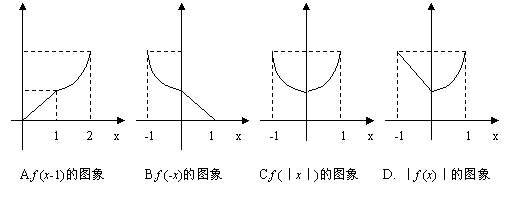
7.已知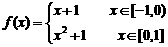 ,则下列函数的图象错误的是 (
)
,则下列函数的图象错误的是 (
)
8定义运算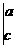
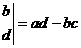 ,若复数
,若复数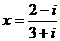 ,
,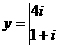
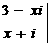 ,则
,则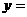 ( )
( )
A. -4 B.4 C.2 D.-2
5. 当n∈N且n≥2时,1+2+22+…+24n-1=5p+q,其中p,q为非负整数,且0≤q<5,则q的值为 ( )
A.0 B.2 C.2 D.与n有关
4.已知l,m,表示直线,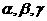 表示平面,下列条件中能推出结论的正确的是( )
表示平面,下列条件中能推出结论的正确的是( )
条件:①l⊥m,l⊥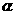 ,m⊥
,m⊥ ②
②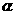 ∥
∥ ,
, ∥
∥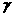 ③l⊥
③l⊥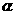 ,
,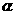 ∥
∥ ; ④ l⊥
; ④ l⊥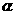 ,m⊥
,m⊥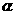
结论:a: l ⊥ b:
b: 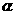 ⊥
⊥ c: l∥m d:
c: l∥m d: 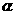 ∥
∥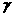
A ①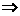 a,②
a,②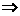 b,③
b,③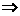 c,④
c,④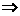 d
B ①
d
B ①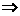 b,②
b,②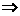 d,③
d,③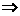 a,④
a,④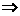 c
c
C ①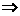 c,②
c,②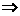 d,③
d,③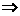 a,④
a,④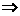 b
D ①
b
D ①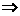 d,②
d,②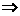 b,③
b,③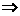 a,④
a,④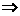 c
c
3. 已知函数y=f(n),(n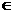 N*),如果7f(n)=f(n-1),f (1)=3,则
N*),如果7f(n)=f(n-1),f (1)=3,则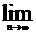 [f(1)+f(2)+…+f(n)]=( )
[f(1)+f(2)+…+f(n)]=( )
A.0 B.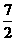 C.
C.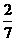 D.3
D.3
2.若 ,则下列结论不正确的是
( )
,则下列结论不正确的是
( )
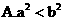

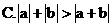
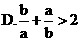
1.命题“若 ,则
,则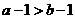 ”的否命题是
( )
”的否命题是
( )
A.若 ,则
,则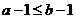 B.若
B.若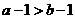 ,则
,则
C.若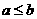 ,则
,则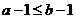 D.若
D.若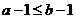 ,则
,则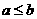
(三)解答题
20.已知两圆C1∶x2+y2+4x-4y-5=0
C2∶x2+y2-8x+4y+7=0
(1)证明此两圆相切,并求过切点的公切线方程.
(2)求过点(2,3)且与两圆相切于上述切点的圆的方程.
21.(1)椭圆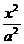 +
+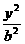 =1上一点P与两焦点 F1F2连线所成的角∠F1PF2=α,求△F1PF2的面积;
=1上一点P与两焦点 F1F2连线所成的角∠F1PF2=α,求△F1PF2的面积;
(2)将上题的椭圆变成双曲线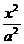 -
-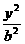 =1 ,求△F1PF2的面积.
=1 ,求△F1PF2的面积.
22.抛物线的顶点在原点,它的准线过双曲线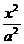 -
-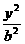 =1的一个焦点,并与双曲线的实轴垂直,又双曲线与抛物线的一个交点是(1.
5,
=1的一个焦点,并与双曲线的实轴垂直,又双曲线与抛物线的一个交点是(1.
5,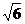 ),求抛物线和双曲线的方程.
),求抛物线和双曲线的方程.
23.已知椭圆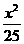 +
+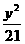 =1,左、右焦点分别为 F2、F1,右准线为L,问能否在椭圆上求得一点P,使│PF1│是P到L的距离d与│PF2│的比例中项?若能,求出P点坐标,若不能,说明理由.
=1,左、右焦点分别为 F2、F1,右准线为L,问能否在椭圆上求得一点P,使│PF1│是P到L的距离d与│PF2│的比例中项?若能,求出P点坐标,若不能,说明理由.
24.试就k的取值(k∈R,且k≠4)讨论方程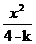 +(k-2)y2=1+k所表 示曲线的形状.
+(k-2)y2=1+k所表 示曲线的形状.
25.已知椭圆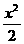 +
+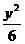 =1中有一内接△PAB,∠X
OP=60°,且kPA+kPB=0
=1中有一内接△PAB,∠X
OP=60°,且kPA+kPB=0
(1)求证:直线AB斜率是定值;
(二)填空题
16.直线xsinα+ycosα=m(常量α∈(0,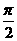 )) 被圆x2+y2=2所截的弦长为
)) 被圆x2+y2=2所截的弦长为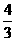
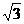 ,则m=________.
,则m=________.
17.设椭圆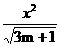 -
-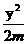 =1的准 线平行于x轴,则m的取值范围是________.
=1的准 线平行于x轴,则m的取值范围是________.
18.如果方程x2cos2θ+y2sinθ=1,表示椭圆,那么θ 角的取值范围是_________.
19.设双曲线C: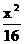 -
-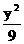 =1椭圆的焦点恰为双 曲线C实轴上的两个端点,椭圆与双曲线离心率为互为倒数,则此椭圆方程是________.
=1椭圆的焦点恰为双 曲线C实轴上的两个端点,椭圆与双曲线离心率为互为倒数,则此椭圆方程是________.
(一)选择题
1.“点M的坐标是方程f(x,y)=0的解”是“点M在方程f(x,y)=0曲线上”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分又非必要条件
2.抛物线x=-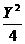 的焦点坐标是( )
的焦点坐标是( )
A.(0,1) B.(-1,0)
C.(0,-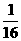 )
D.(-
)
D.(-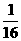 ,0)
,0)
3.椭圆(1-m)x2-my2=1的长轴长是( )
A.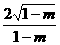 B.
B. 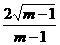
C. 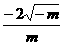 D.
D.
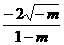
4.下列各对双曲线中,既有相同离心率又有相同渐近线的是( )
A. -y2=1和
-y2=1和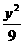 -
- =1
=1
B.  -y2=1和y2-
-y2=1和y2- =1
=1
C.y2- =1和x2-
=1和x2-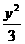 =1
=1
D.  -y2=-1和
-y2=-1和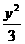 -
-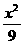 =1
=1
5.抛物线x2-4y=0上一点P到焦点的距离为3,那么P的纵坐标是( )
A.3
B.2
C.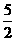 D.-2
D.-2
6.已知椭圆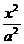 +
+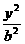 =1 (a>b>0)的两 个焦点把夹在两条准线间的线段三等分,那么这个椭圆的离心率是( )
=1 (a>b>0)的两 个焦点把夹在两条准线间的线段三等分,那么这个椭圆的离心率是( )
A.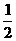 B.
B. 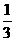 C.
C.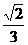 D.
D. 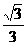
7.圆x2+y2-2axsinα-2bycosα-a2cos2α=0在x轴上截得的弦长是( )
A.2a B.2│a│ C.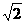 │a│ D.4│a│
│a│ D.4│a│
8.过双曲线的一个焦点,有垂直于实轴的弦PQ,F′是另一个焦点,若∠PF′Q=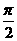 ,则双曲线离心率是( )
,则双曲线离心率是( )
A.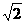 +2 B.
+2 B. 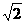 +1 C.
+1 C. 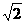 D.
D. 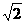 -1
-1
9.抛物线y2+4y-4x=0的准线方程是( )
A.x=0 B.y=0 C.x=-2 D.y=-2
10.椭圆的两准线方程分别为x= ,x=-
,x=-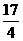 ,一个 焦点坐标为(6,2),则椭圆方程是( )
,一个 焦点坐标为(6,2),则椭圆方程是( )
A.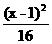 +
+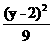 =1
=1
B.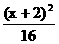 +
+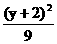 =1
=1
C.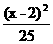 +
+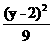 =1
=1
D.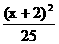 +
+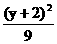 =1
=1
11.设双曲线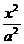 -
-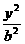 =1的两条渐近线含 实轴的夹角为θ,而离心率e∈[
=1的两条渐近线含 实轴的夹角为θ,而离心率e∈[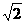 ,2],则θ的取值范围是( )
,2],则θ的取值范围是( )
A.[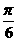 ,
,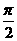 ]
B.[
]
B.[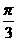 ,
,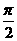 ]
]
C.[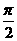 ,
,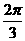 ]
D.[
]
D.[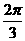 ,π]
,π]
12.椭圆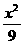 +
+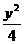 =1的弦AB被点(1,1)平分,则 AB所在的直线方程是( )
=1的弦AB被点(1,1)平分,则 AB所在的直线方程是( )
A.4x-9y-11=0 B.4x+9y-13=0
C.9x+4y-10=0 D.9x-4y-5=0
13.和x轴相切,且和圆x2+y2=1外切的动圆圆心的轨迹方程是( )
A.x2=2y+1 B.x2=-2y+1
C.x2=2y+1或x2=-2y+1 D.x2=2│y│+1
14.如果椭圆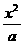 +
+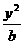 =1 (a>b>0)和曲线
=1 (a>b>0)和曲线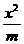 +
+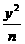 =1(m>0,n>0)有相同的焦点F1和F2 ,P是这两条曲线的交点,则│PF1│·│PF2│的值是( )
=1(m>0,n>0)有相同的焦点F1和F2 ,P是这两条曲线的交点,则│PF1│·│PF2│的值是( )
A.a-m
B.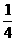 (a-m)
(a-m)
C.a2-m2
D.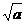 -
-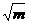
15.已知0<a<1<b,那么曲线a2x2-a2y2=logab是( )
A.焦点在x轴的双曲线
B.焦点在y轴的椭圆
C.焦点在x轴的等轴双曲线
D.焦点在y轴的等轴双曲线
20.(本小题满分14分)
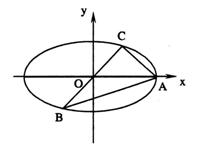 已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆中心O,如图,且
已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆中心O,如图,且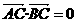 ,|BC|=2|AC|.
,|BC|=2|AC|.
(1) 求椭圆的方程;
(2) 如果椭圆上两点P、Q使∠PCQ的平分线垂直AO,则总存在实数λ,使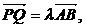 请给出证明.
请给出证明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com