
题目列表(包括答案和解析)
3. (2005全国卷II文第5题)抛物线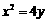 上一点
上一点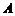 的纵坐标为4,则点
的纵坐标为4,则点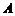 与抛物线焦点的距离为
( )
与抛物线焦点的距离为
( )
(A) 2 (B) 3 (C) 4 (D) 5
1. (2005全国卷Ⅰ文第6题) 已知双曲线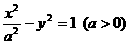 的一条准线为
的一条准线为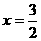 ,则该双曲线的离心率为
( )
,则该双曲线的离心率为
( )
(A)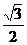 (B)
(B)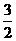 (C)
(C)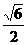 (D)
(D)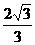
2 (2005全国卷Ⅰ理第6题) 已知双曲线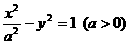 的一条准线与抛物线
的一条准线与抛物线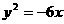 的准线重合,则该双曲线的离心率为
( )
的准线重合,则该双曲线的离心率为
( )
(A)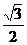 (B)
(B)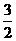 (C)
(C)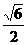 (D)
(D)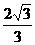
23.[(甘肃贵州宁夏青海新疆)·理科数学第21题(12分),文科数学第22题(14分)]
双曲线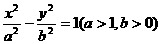 的焦距为2c,直线
的焦距为2c,直线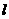 过点(a,0)和(0,b),且点(1,0)到直线
过点(a,0)和(0,b),且点(1,0)到直线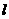 的距离与点(-1,0)到直线
的距离与点(-1,0)到直线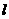 的距离之和
的距离之和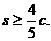 求双曲线的离心率e的取值范围.
求双曲线的离心率e的取值范围.
22.[(陕西广西海南西藏内蒙古)·理科数学第21题(12分),文科数学第22题(14分)]
设椭圆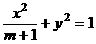 的两个焦点是
的两个焦点是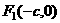 与
与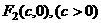 ,且椭圆上存在一点
,且椭圆上存在一点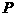 ,使得直线
,使得直线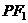 与
与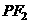 垂直.
垂直.
(1)求实数 的取值范围;
的取值范围;
(2)设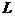 是相应于焦点
是相应于焦点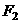 的准线,直线
的准线,直线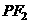 与
与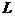 相交于点
相交于点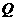 ,若
,若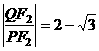 ,求直线
,求直线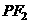 的方程.
的方程.
21.[ (四川云南吉林黑龙江)· 理科数学第21题(12分),文科数学第22题(14分)]
给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点。
(Ⅰ)设l的斜率为1,求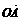 与
与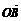 的夹角的大小;
的夹角的大小;
(Ⅱ)设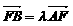 ,若λ∈[4,9],求l在y轴上截距的变化范围.
,若λ∈[4,9],求l在y轴上截距的变化范围.
20.[(山东山西河南河北江西安徽)·理科数学第21题(12分),文科数学第22题(14分)]
设双曲线C: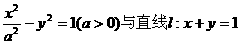 相交于两个不同的点A、B.
相交于两个不同的点A、B.
(I)求双曲线C的离心率e的取值范围:
(II)设直线l与y轴的交点为P,且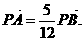 求a的值.
求a的值.
19.[2004年全国高考(甘肃贵州宁夏青海新疆)·理科数学第16题,文科数学第16题]
设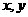 满足约束条件:
满足约束条件:
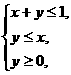 则
则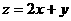 的最大值是
.
的最大值是
.
18.[2004年全国高考(甘肃贵州宁夏青海新疆)·理科数学第8题]
已知椭圆的中心在原点,离心率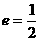 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线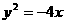 的焦点重合,
的焦点重合,
则此椭圆方程为 ( )
A.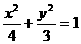 B.
B.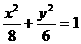 C.
C.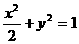 D.
D.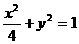
17.[2004年全国高考(甘肃贵州宁夏青海新疆)·文科数学第8题]
已知圆C的半径为2,圆心在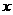 轴的正半轴上,直线
轴的正半轴上,直线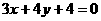 与圆C相切,则圆C的方程为 ( )
与圆C相切,则圆C的方程为 ( )
A.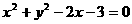 B.
B.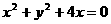
C.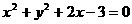 D.
D.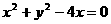
16.[2004年全国高考(甘肃贵州宁夏青海新疆)·文科数学第7题]
已知函数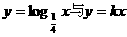 的图象有公共点A,且点A的横坐标为2,则
的图象有公共点A,且点A的横坐标为2,则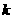 = ( )
= ( )
A.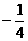 B.
B.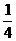 C.
C.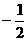 D.
D.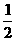
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com